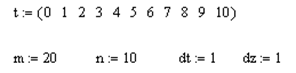|
|
Модель идеального вытеснения
Цель работы: изучить реальные процессы, которые могут быть аппроксимированы при исследовании модели идеального вытеснения.
Теоретические сведения Модель идеального вытеснения относится к классу моделей с распределенными параметрами. Для таких моделей характерно, что переменные процесса могут изменяться как во времени, так и в пространстве, или только в пространстве. Их математическое описание включает обычно дифференциальные уравнения в частных производных, либо обыкновенные дифференциальные уравнения в случае стационарных процессов с одной пространственной переменной. Примером процесса, описываемого такими моделями, служит трубчатый аппарат с большим отношением длины к диаметру и значительной скоростью движения реагентов (рис. 1).
В основе модели идеального вытеснения лежит допущение о поршневом течении, без перемешивания вдоль потока при равномерном распределении вещества в направлении, перпендикулярном движению потока. Время пребывания всех частиц в системе одинаково и равно отношению объема системы (аппарата) к объемному расходу жидкости. Такой поток, например, имеет место в трубчатом аппарате при турбулентном режиме течения жидкости через него. Математическое описание модели идеального вытеснения (см. рис. 1) имеет вид
где t - исследуемый интервал времени, с; x - координата, вдоль которой передвигается вещество и вдоль которой исследуется изменение концентрации; w - линейная скорость передвижения вещества (м/с), Для решения дифференциального уравнения в частных производных (1) начальное условие: в начальный (нулевой) момент времени по всей длине аппарата начальная концентрация была равна некоторому начальному значению cн, т. е. cвых(0, x) = cн(x), при t = 0, 0 < x < граничное условие: концентрация в начале аппарата в любой момент времени есть некоторая входная функция от времени, т. е. свых(t, 0) = cвх(t), при x = 0, t > 0. (3) Решение уравнения (1), удовлетворяющее условиям (2) и (3), имеет вид
Из решения (4) следует, что любое изменение концентрации на входе в аппарате идеального вытеснения появляется на его выходе через время, равное среднему времени пребывания Аппарат идеального вытеснения аппроксимируют звеном чистого запаздывания. Передаточная функция этого звена имеет вид
где Виды выходных сигналов при различных входных воздействиях представлены на рис. 2.
Задание. (Исходные данные в приложении 3.)
1. Составить аналитическую модель описания процесса. 2. Составить модель решения и записать ее в аналитическом виде. 3. Разработать алгоритм поиска решения. 4. Получить выходные данные. 5. Построить графическую интерпретацию полученного решения.
Порядок выполнения работы 1. Записать словесную постановку задачи в соответствии с заданием варианта, выданного преподавателем. 2. Составить аналитическую модель описания задачи. 3. Разработать математическую модель решения. 4. Решить задачу с исходными данными, соответствующими вашему варианту. Получить выходные данные. 5. По выходным данным построить графики зависимости выходного параметра во времени в указанном интервале.
Пример расчета Условие. В проточный аппарат трубчатого вида диаметром d = 0,05 м и длиной
При этом концентрация вещества в начале аппарата в любой момент времени есть некоторая входная функция от времени, изменяющаяся по следующему закону: Решение
1. Словесная постановка задачи. Исходными данными рассматриваемого процесса являются: - диаметр трубчатого аппарата d = 0,05 м; - длина аппарата - объемный поток n = 1,7 м3/ч; - начальная концентрация вещества по всей длине аппарата в момент времени t = 0 была равна начальному значению c (0) = cн = 10; - концентрация вещества в начале аппарата в любой момент времени равна концентрации вещества во входном потоке - исследуемый интервал времени T = [0, 2]. 2. Синтез аналитической модели описания. Для рассматриваемого процесса, проходящего в аппарате (см. рис. 3), принимаем следующие допущения: - диаметр намного меньше длины (d<< - в поперечном направлении в каждом слое осуществляется идеальное смешение; - в продольном направлении перемешивание отсутствует, т. е. вытеснение идеальное. Концентрация исследуемого вещества в потоке аппарата зависит от двух переменных: 1) концентрация изменяется во времени на каждом бесконечно малом интервале сечения (Dx); 2) каждый момент времени происходит изменение концентрации вещества по всей длине рассматриваемого аппарата. Следовательно, исследуемая концентрация есть функция двух переменных - времени (t) и координаты длины аппарата (x), т. е. cвых = f(t,x). При исследовании динамики изменения cвых по обеим переменным может быть использовано дифференциальное уравнение 1-го порядка в частных производных. Исходя из вышесказанного, для описания структуры потока в аппарате (см. рис. 3) применяем следующую математическую модель:
где w - линейная скорость передвижения вещества (м/ч),
где S - площадь поперечного сечения аппарата (м2).
Для решения дифференциального уравнения в частных производных (5) запишем начальное и граничное условия: - начальное условие: свых(x, 0) = cн=10, при t = 0, 0 < x < - граничное условие: свых(0, t) = 3. Разработка модели решения. Математическая модель исследуемого процесса записана в виде дифференциального уравнения 1-го порядка в частных производных (5) с начальным и граничным условиями (6) и (7) соответственно. Для решения воспользуемся методом конечных разностей. Левая часть уравнения (5) представляет собой производную по времени t (T=[0,2)). В конечных разностях она примет вид:
где Dt - бесконечно малый промежуток интервала времени, Правая часть уравнения (5) представляет собой производную по координате длины аппарата x (x=[0,
где Dx - бесконечно малый участок сечения аппарата, Алгоритм вывода численного решения уравнения (5).
Введем обозначения
Заменим в уравнении
Таким образом, численное решение уравнения (5), основанное на методе конечных разностей, примет вид
Начальное (6) и граничное (7) условия в конечных разностях будут иметь вид: - начальное условие: - граничное условие: Необходимым условием сходимости метода конечных разностей является условие
Так как
Задаваясь одним из параметров (n или m), определяется другой. Например, если примем n = 100, тогда из условия (12) имеем:
Аналогично, задаваясь параметром m=const, определим параметр n. Таким образом, модель решения уравнения (5) с начальным (6) и граничным (7) условиями будет состоять из (8), (9), (10), (11).
4. Решение задачи в среде MathСad. Введем исходные данные задачи (рис. 4).
Рис. 4. Ввод исходных данных
Рассчитаем значение концентрации исходного вещества на входе в аппарат в каждой точке разбиения интервала времени. Для определения выражений, переменных и функций в несколько строк (при возвращении различных значений, как в нашем случае) в системе MathCAD используются программные модули. Для вставки программного кода в документы используется специальная панель инструментов Programming (Программирование, рис. 5), которую можно вызвать на экран нажатием кнопки Programming Toolbar на панели Math (Математика).
Рис. 5. Панель инструментов Programming Присваивание в пределах программ, в отличие от остальных документов MathСAD, производится с помощью оператора Local Definition(Локальное присваивание), который вставляется нажатием кнопки с изображением стрелки на панели Programming. Ни оператор присваивания «:=», ни оператор вывода «=» в пределах программ не применяются. Определим с помощью программы функцию свх(t) (рис. 6).
Рис. 6. Вычисление значений функции свх(t) Программный модуль обозначается в MathСAD вертикальной чертой, справа от которой последовательно записываются операторы языка программирования. Чтобы создать программный модуль (см. рис. 6): 1. Введите часть выражения, которая будет находиться слева от знака присваивания и сам знак присваивания. В нашем примере это имя функции cv. 2. При необходимости вызовите на экран панель инструментов Programming (Программирование) (см. рис. 5). 3. Нажмите на этой панели кнопку Add Line (Добавить линию). 4. Если приблизительно известно, сколько строк кода будет содержать программа, можно создать нужное количество линий повторным нажатием кнопки Add Line (Добавить линию) соответствующее число раз (рис.).
Рис. 7. Начало создания программного модуля
5. В появившиеся местозаполнители введите желаемый программный код, используя программные операторы. В нашем примере в верхнем местозаполнителе вводим оператор For (при этом автоматически добавляется местозаполнитель для записи тела цикла), имя параметра цикла и диапазон его значений. В появившейся строке с помощью оператора Local Definition, вводим тело цикла, т. е. выражение, которое должно выполняться циклически. В нижнем местозаполнителе записано имя заполняемого массива. Заметим, что переменная s существует только внутри программы, выделенной вертикальной чертой. Из других мест документа получить ее значение невозможно. После того как программный модуль полностью определен, и ни один местозаполнитель не остался пустым, функция может использоваться обычным образом, как в численных, так и в символьных расчетах. Для того чтобы вывести посчитанные значения после программного кода, введем выражение “cv=” и нажмем клавишу Enter, на экран будет выведена таблица решений (см. рис. 6). Далее для решения дифференциального уравнения в частных производных (5) запишем начальное и граничное условия (6), (7) и численное решение уравнения (5) – формулу (10). Для этого необходимо записать следующий программный код (рис. 8).
Рис. 8. Заполнение массива концентрации исходного вещества
Для вывода посчитанных значений, запишем выражение “cw=” и нажмем клавишу Enter (рис. 9). 5. Построение графиков. Теперь по полученным данным построим графики зависимости выходного параметра во времени в указанном интервале. Сначала построим график изменения концентрации по длине аппарата в конечный момент времени. Для этого на макете для построения графиков в позиции оси абсцисс вводим параметр i, пределы изменения которого задаются перед построением, а в положении оси ординат – обозначение последнего столбца матрицы значений функции свых(t) (рис. 10).
Рис. 9. Массив концентрации исходного вещества
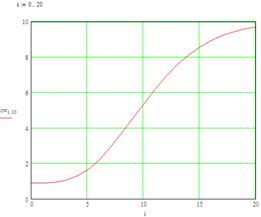
Рис. 10. Зависимость распределения концентрации вещества свых(t) по длине аппарата в момент времени t = 2 ч
Аналогично строим график изменения концентрации исходного вещества в конце аппарата в каждый момент времени, при этом на оси абсцисс отображается изменение параметра j (начальное и конечное значение которого предварительно задаются), на оси ординат – интересующие нас значения выходного параметра, что соответствует последней строке матрицы значений функции свых(t) (рис. 11).
  
Рис. 11. Зависимость распределения концентрации вещества свых(t) в каждый момент времени t в конце аппарата Контрольные вопросы и задания
1. Как записывается аналитическая модель описания процесса идеального вытеснения? 2. Каковы начальные условия процесса идеального вытеснения? 3. Как записывается модель решения для процесса идеального вытеснения? 4. Какие численные методы используются для решения обыкновенных дифференциальных уравнений и систем дифференциальных уравнений? 5. Каковы особенности модели решения для процесса идеального вытеснения? 6. Рассказать о программировании в среде MathСAD. 7. Назвать способ построения графиков в MathСAD.
Лабораторная работа № 4 Комбинированные задачи Цель работы: изучить реальные процессы, которые могут быть аппроксимированы при исследовании комбинированных моделей процессов идеального смешения и идеального вытеснения.
Задание. (Исходные данные в приложении 4.)
1. Составить аналитическую модель описания процесса. 2. Составить модель решения и записать ее в аналитическом виде. 3. Разработать алгоритм поиска решения. 4. Получить выходные данные. 5. Построить графическую интерпретацию полученного решения. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

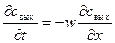 , (1)
, (1)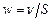 , где S - площадь поперечного сечения аппарата (м2).
, где S - площадь поперечного сечения аппарата (м2). , (2)
, (2)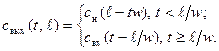 (4)
(4)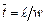 , где
, где  ,
, - время транспортного запаздывания.
- время транспортного запаздывания.



 . Определить концентрацию вещества в аппарате cвых(t) по его длине в момент времени T = 2 ч.
. Определить концентрацию вещества в аппарате cвых(t) по его длине в момент времени T = 2 ч. ;
; , (5)
, (5) ,
,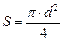 , тогда
, тогда 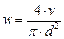 .
.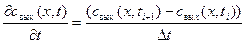 ,
, , где n - число разбиений интервала времени; i - номер интервала разбиения, целые числа, i = 0, 1, 2, …, (n-1), n.
, где n - число разбиений интервала времени; i - номер интервала разбиения, целые числа, i = 0, 1, 2, …, (n-1), n.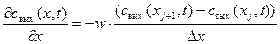 ,
,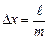 , где m - число разбиений аппарата по длине; j - номер интервала разбиения, целые числа, j = 0, 1, 2, …, (m-1), m.
, где m - число разбиений аппарата по длине; j - номер интервала разбиения, целые числа, j = 0, 1, 2, …, (m-1), m.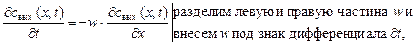


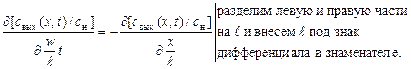
 - безразмерная координата длины;
- безразмерная координата длины;  - безразмерная координата концентрации;
- безразмерная координата концентрации; 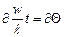 - безразмерная координата времени. Тогда, уравнение (5), начальное условие (6) и граничное условие (7) примут вид
- безразмерная координата времени. Тогда, уравнение (5), начальное условие (6) и граничное условие (7) примут вид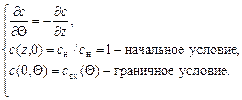
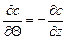 частные дифференциалы левосторонними конечными разностями относительно
частные дифференциалы левосторонними конечными разностями относительно 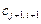 :
:
 . (8)
. (8) ; (9)
; (9)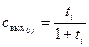 . (10)
. (10)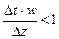 .
.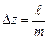 и
и  , получаем условие выбора значений интервалов n и m:
, получаем условие выбора значений интервалов n и m: . (11)
. (11)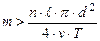 .
.