
|
|
Динамические характеристики системы в тактовые моменты времени12 Цифровое (микропроцессорное) управление - это управление, при котором данные измерений и сигналы управления, формируемые вычислительной машиной, поступают только в виде дискретных значений с заранее определенным временным интервалом следования. Этот временной интервал Т называется периодом дискретизации (квантования). При этом значение сигнала после аналого-цифрового преобразования и до выхода из вычислительной машины представляется в виде машинного слова - дискретного сигнала, который в двоичной системе кодирует несколькими разрядами значение исходного аналогового сигнала в определенные тактовые моменты времени iT. В простых регуляторах, таких, как, например, ПИД (пропорционально-интегрально-дифференциальный)-регулятор, период квантования Т определяется затратами времени на аналого-цифровое и цифроаналоговое преобразования сигналов. В тех случаях, когда объем и сложность вычислений по задачам управления возрастают, требуя применения микропроцессора либо вычислительной машины под периодом квантования (дискретизации) обычно понимается время, затрачиваемое на выполнение требуемых вычислений, а затраты времени на аналого-цифровое и цифроаналоговое преобразования либо не учитываются совсем, либо оцениваются приближенно.
ЦАП Фиксатор Объект управления
ЦВМ
АЦП T x(t) либо y(t) x[i] либо y[i] a)
T u[i] ЦАП u(t) Объект управления y(t) Объект управления
Процессор Интерфейс
АЦП Выборка и хранение
x[i] либо y[i]
T б) Рис 1.4 Функциональная схема системы цифрового управления. (а) обобщенная схема системы цифрового управления. (6) Схема цифрового управления с фиксатором (экстраполятором) нулевого порядка. ЦАП - цифроаналоговый прео6разователь; АЦП аналого-цифровой прео6разователь. С выхода объекта управления через аналого-цифровой преобразователь (АЦП) в вычислительную машину поступает либо сигнал x[t] = х(iT), либо сигнал y[t] = у(iT) с интервалом времени Т. Микропроцессор обрабатывает эти сигналы и вычисляет управляющее воздействие, значения которого через каждый интервал времени т после цифроаналогового преобразования возобновляются в экстраполяторе (фиксаторе). Затем управляющее воздействие передается на объект управления. Под экстраполятором понимается схема преобразования дискретного сигнала в непрерывный сигнал. Подобный экстраполятор обычно называется фиксатором нулевого порядка, если его выходной сигнал поддерживается на интервале времени Т постоянным (рис. 1.4 а). В отличие от такого фиксатора в экстраполяторе первого порядка (рис. 1.4 б) осуществляется обобщение дискретных данных на интервале времени т по предыдущей и текушей выборкам. Очевидно, что в зависимости от типа экстраполятора меняется и дискретная модель объекта управления.
u(t) u[2] u[2] u[0] u[0] u[1] u[1]
u(t)
u[0] u[2] u[1] 0 T 2T 3T t б)
Рис. 1.5 Характеристики сигналов на входе и выходе экстраполятора нулевого (а) и первого (б) порядков.
На современном уровне развития микропроцессорной технологии наибольшее распространение в практике получил фиксатор нулевого порядка. В этом случае цифровой сигнал хранится в памяти накопителя (триггерного типа) на протяжении периода Т, и через цифроаналоговый преобразователь непрерывно, в течение времени Т выдается на объект управления постоянный по величине аналоговый сигнал (рис. 1.5 б). Такая организация работы экстраполятора требует периодического, через каждый интервал времени Т обновления содержимого памяти. Аналого-цифровые преобразователи осуществляют дискретную выборку данных из входного аналогового сигнала и выполняют роль интерфейса между объектом управления и вычислительной машиной (рис. 1.4). Рассмотрим теперь математическую модель в виде уравнения состояния, согласно выражению (1.26), дискретной системы управления аналоговым объектом с учетом использования фиксатора нулевого порядка. Для этого установим взаимосвязь между сигналами u[i] и х[i] либо y[i], воспользовавшись схемой, где входная часть фиксатора нулевого порядка представляет собой дискретизатор и аналого-цифровой преобразователь, а выходная часть цифроаналоговый преобразователь. Пусть u[i] - дискретный сигнал, тогда непрерывный, или аналоговый, сигнал u[t], поступающий на объект управления и являющийся выходным сигналом фиксатора нулевого порядка, удовлетворяет соотношению (см. рис. 1.6).
Обозначим переменную состояния объекта управления и выходную переменную при t = iT через х [i] и у[i] соответственно, причем
u[i] Фиксатор u(t) Объект y(t) нулевого порядка управления x[i] либо y[i]
Рис. 1.6 Функциональная схема взаимосвязи дискретных и непрерывных сигналов в системе цифрового управления
x[1] x[2]
x[3] x[0]
u[1] u[2] u[0]
0 T 2T 3T t Рис. 1.7 Значения переменных в дискретные моменты времени. с учетом этого можно записать
где
Решение уравнения состояния по аналогии с выражением (1.33) и с учетом того, что t0 = iT, t = (i + 1) Т, будет иметь вид
Очевидно, что если на каждом временном интервале интегрирования Т, u(t) представляет собой постоянную величину u[i], то, преобразуя переменную интегрирования δ= (i + 1)Т - т, получаем тождественность выражений (1.40) и (1.39 б). При этом выражение (1.39 б) получается в результате прямой дискретизации выражения (1.26 б). Уравнения (1.39) называются уравнением состояния и уравнением выхода дискретной системы. Эти уравнения определяют динамические характеристики системы в тактовые моменты времени и графически могут быть представлены в виде структурной схемы, где оператор Z Решение уравнения (1.39 б) легко получить из следующей вектор ной рекуррентной формулы:
b z-1In c +
A
Рис. 1.8 Структурная схема дискретной системы в пространстве состояний Уравнение (1.39) удобно использовать при моделировании непрерывной системы. В этом случае период квантования Т выбирается достаточно малым, с тем, чтобы на периоде Т входную величину u(t) в выражении (1.26) считать постоянной. Значения х[i] определяются численным методом по рекуррентной формуле (1.41) с помощью соотношений (1.30) и (1.32 в) для определения матричной показательной функции и соответствующих интегралов. Рассмотрим процесс нахождения матриц перехода на конкретном примере. Пример 1.7 Пусть в системе, приведенной в примере 1.6, используется фиксатор нулевого порядка и дискретизация осуществляется с периодом квантования Т = 1. Требуется найти матрицы коэффициентов А, b, c для дискретной модели. В примере 1.6 было найдено выражение
Учитывая, что
Подставляя t = Т = 1, согласно соотношениям (1.39), будем иметь
Вычислительные методы
Поскольку назначением математической модели является предсказание реакции системы на выбранные входные сигналы, мы должны уметь и оценивать начальные условия для уравнения модели, и решать дифференциальные уравнения. Опишем методы предсказания и коррекции и Рунге-Кутта для решения дифференциальных уравнений и покажем, каким образом по методу Рунге-Кутта высшего порядка можно получить высокую точность.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 T u[i] u(t) x(t) либо y(t)
T u[i] u(t) x(t) либо y(t) x(t) либо
x(t) либо информации
информации 0 T 2T t a) 0 T 2T 3T t
0 T 2T t a) 0 T 2T 3T t ,
, 

 ,
, 
 x(t) либо T
x(t) либо T x(t)
x(t)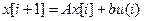 ,
,  (1.39 а)
(1.39 а) (1.39 б)
(1.39 б) ,
, 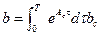 ,
,  (1.39 в)
(1.39 в) (1.40)
(1.40) - оператор запаздывания на один такт (период), а матрица А, определяющая переход переменной состояния x[i] в x[i + 1], - матрица перехода состояния.
- оператор запаздывания на один такт (период), а матрица А, определяющая переход переменной состояния x[i] в x[i + 1], - матрица перехода состояния.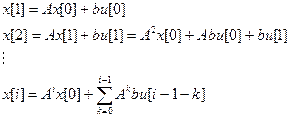 (1.41)
(1.41) u[i] + x[i+1] x[i] y[i]
u[i] + x[i+1] x[i] y[i] в виде
в виде
 получим
получим
 ,
,  ,
, 