
|
|
Производные высших порядков
Если производная у' =φ(х) от функции у =f (х) дифференцируема, то от нее, в свою очередь, можно вычислить производную, которая называется производной второго порядка или второй производной от заданной функции по аргументу х. Ее обозначение у'', Возможно образование производных и более высоких порядков: у''', (или Производная второго порядка от заданной функции у=f (х) вычисляется путем последовательного двукратного дифференцирования заданной функции по общим правилам:
у =f (х); у' = f' (х)=φ(х); у''= f'' (х)=φ'(х) Пример. у=х4, у'=4х3, у''=12 х2 Физический смысл производной второго порядка – это мгновенное (в заданный момент времени) значение ускорения при прямолинейном неравномерном движении тела.
Таблица 1. Производные основных элементарных функций Действительно, скорость
Пример 2. Задано уравнение движения тела S=2t2 (м). Найти скорость и ускорение через 5 с после начала движения. Решение: Скорость
Дифференциал функции Из уравнения (4) можно записать равенство
где Преобразовав (6) имеем:
Из (7) видно, что приращение функции состоит из двух слагаемых. Слагаемое Дифференциал функции равен произведению производной функции на приращение аргумента и символически обозначается
Рис.2
Таким образом, дифференциал функции, в общем случае отличаясь от приращения функции, представляет собой главную часть этого приращения, линейную относительно приращения аргумента. В этом заключается аналитический смысл дифференциала. Отсюда следует, что при достаточно малых приращениях аргумента величина приращения функции приближенно равна дифференциалу этой функции:
Для выяснения геометрического смысла дифференциала рассмотрим график функции Таким образом, дифференциал функции является приращением ординаты касательной (АВ), которое соответствует приращению Дифференциалом аргумента называют приращение аргумента, т.е.
С учетом (10) можно записать:
Применение дифференциала функции в приближенных вычислениях Применение дифференциала функции в приближенных вычислениях основано на использовании формулы (9), которая справедлива при достаточно малых приращениях аргумента функции
откуда
Формулу (12) можно использовать при нахождении приближенных значений функций. Пример 3.Найти приближенно значение функции
для значения ее аргумента, равного 16,02. Решение. Найдем производную данной функции:
и подставим в формулу (12):
Положим
Понятие неопределенного интеграла
Функция F(x) называется первообразнойфункции f(x) на интервале (a,b), если она дифференцируема на этом интервале и в каждой его точке F´(x)=f(x), (13)
Например, первообразными функции 4x3 являются функции x4 и x4+6, так как
(x4)'=4x3 и (x4+6)'=4x3
Заметим, что вообще, если F(x) первообразная f(x) , то F(x)+C , где C - произвольная постоянная, также является первообразной f(x) , так как
(F(x)+C)'=F'(x)=f(x), (14)
Совокупность всех первообразных функции f(x) называется неопределенным интегралом от функции f(x) . Он обозначается символом
Функция f(x) называется подынтегральной функцией, f(x)dx - подынтегральным выражением. Если F(x) - какая-нибудь первообразная функции f(x), то
где C - произвольная постоянная. Нахождение неопределенного интеграла называется интегрированием функции f(x). Чтобы найти интеграл, надо выполнить действия, обратные дифференцированию.
Основные свойства неопределенного интеграла
1. 2.d
3.
4.
5.
6.
где k - постоянный множитель, отличный от нуля.
Таблица основных интегралов
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Методы интегрирования На практике при вычислении неопределенных интегралов их стараются свести к табличному виду различными методами. Рассмотрим некоторые из них.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
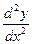 ,
,  .
. ) и т.д.
) и т.д.
 , а ускорение есть изменение скорости, т.е.
, а ускорение есть изменение скорости, т.е. а=υ'=S'' или
а=υ'=S'' или  .
. Ускорение
Ускорение  .
. , (6)
, (6) - некоторая малая величина. При
- некоторая малая величина. При 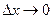
 , т.е.
, т.е. 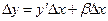 , (7)
, (7)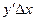 называют главной частью приращения функции
называют главной частью приращения функции  или дифференциалом функции.
или дифференциалом функции. :
: , (8)
, (8)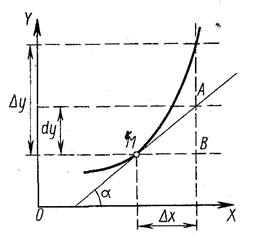 -
- , (9)
, (9) АВМ. Катет МВ равен приращению аргумента
АВМ. Катет МВ равен приращению аргумента  ;
;  ;
;  . Итак,
. Итак,  .
. , (10)
, (10)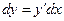 , (11)
, (11) представить в виде
представить в виде  , а дифференциал в виде
, а дифференциал в виде 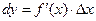 , то будем иметь:
, то будем иметь: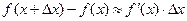 ,
, , (12)
, (12)
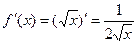
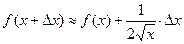 .
. , а
, а  . Тогда
. Тогда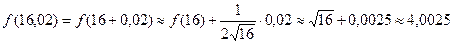 .
.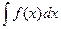
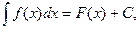 (15)
(15)

 ;
; ;
; ;
; ;
; ;
; ,
, 
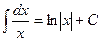 ;
; ; (a> 0, a
; (a> 0, a 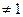 )
) ;
; ;
;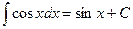 ;
;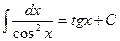 ;
; ;
;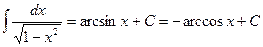 ;
; ;
;