
|
|
Тригонометрическая форма записи комплексных чисел.
Это запись комплексного числа в виде
где r – модуль комплексного числа, j - аргумент. Примечание: если комплексное число записано в виде
то это означает, что угол φ отрицательный и данное число надо записать в виде:
Рис.4.1. Геометрическая интерпретация комплексного числа Модуль комплексного числа:
Аргументкомплексного числа (j) - величина угла между положительным направлением действительной оси и вектором, соответствующим комплексному числу.
Аргумент зависит от того, в какой координатной четверти лежит вектор, соответствующий этому комплексному числу:
Пример. Перевести число Решение: a = 3,
Так как
Тогда, тригонометрическая форма записи имеет вид:
Действия над комплексными числами в тригонометрической форме: 1.
2. 3. Пример.Выполнить действия над комплексными числами в тригонометрической форме: А)
Б)
Экспоненциальная (показательная) форма записи комплексных чисел. Это запись комплексного числа в виде
где r – модуль комплексного числа, j - аргумент
Действия над комплексными числами в показательной форме: 1. 2. 3. 4. Пример.Выполнить действия над комплексными числами в экспоненциальной (показательной) форме записи: А) Б) В)
Лекция 5. ПРЕДЕЛ ФУНКЦИИ Пусть функция y=f(x) определена в некоторой окрестности точки a. Предположим, что независимая переменная x неограниченно приближается к числу a. Это означает, что мы можем придавать х значения сколь угодно близкие к a, но не равные a. Будем обозначать это так x → a. Для таких x найдем соответствующие значения функции. Может случиться, что значения f(x) также неограниченно приближаются к некоторому числу А. Тогда говорят, что число А есть предел функции f(x) при x → a. Число A называется пределом функции f( x ) в точке a , если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a , и для каждого ε > 0 существует δ > 0 такое, что для всех x , удовлетворяющих условию | x – a | < δ, x ≠ a , выполняется неравенство | f ( x ) – A | < ε. Если A – предел функции в точке a , то пишут, что
Теоремы о пределах(правила предельного перехода) 1. Предел суммы или разности равен сумме или разности пределов.
2. Предел произведения равен произведению пределов.
3. Предел отношения равен отношению пределов.
Свойства пределов
1. Предел постоянной равен этой постоянной. Lim A=A , если А = const 2. Постоянную можно вынести за знак предела.
В теории пределов существуют следующие соотношения:
Основные неопределенности: 1. Чтобы раскрыть неопределенность
n – наивысшая степень числителя, m – наивысшая степень знаменателя, а – отношение коэффициентов при х в наивысшей степени. 2. Чтобы раскрыть неопределенность 3. Чтобы раскрыть неопределенность Замечательные пределы: Первый замечательный предел:предел отношения sin бесконечно малой величины к самой этой величине равен 1.
Свойства: 1. 2. 3. Второй замечательный предел:
Частный случай:
Пример. А)
Б)
В)
Д)
Лекция 6. ПРОИЗВОДНАЯ ФУНКЦИИ
Пусть функция f(x) определена в некоторой окрестности точки x0. Производной функции f(x) в точке x0 называется предел отношения приращения функции ∆f(x0) к приращению аргумента ∆х, при ∆х→0, если этот предел существует, и обозначается f '(x0).
Рис. 6.1. График дифференцируемой функции
Операция нахождения производной называется дифференцированием функции.
Функция, имеющая производную в точке х0, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке интервала (а;b), называется дифференцируемой на этом интервале. Правила дифференцирования: Пусть U, V - дифференцируемые функции независимой переменной х , С – константа, тогда: 1) 2) 3) 4) Пример.Найти производную функции А) Б) В) Г) Решение: А)
Б) В)
Г) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ,
,


 или
или 
 из алгебраической формы записи в тригонометрическую.
из алгебраической формы записи в тригонометрическую.

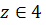 четверти следовательно,
четверти следовательно,
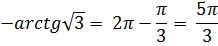
 .
.
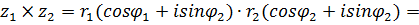


 - формула Муавра
- формула Муавра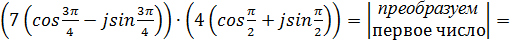



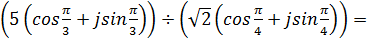

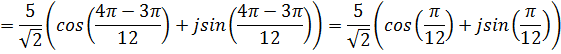
 ,
,


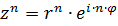

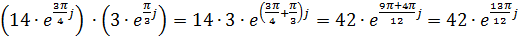






 , если С = const
, если С = const
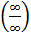
 , где
, где
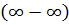
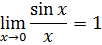



 или
или 
 ;
; 






 Г)
Г) 

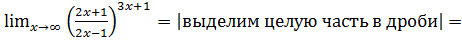
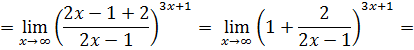





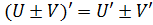


 ;
; ;
; ;
; .
.
 .
.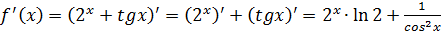 .
.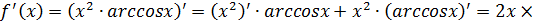
 .
. .
.