
|
|
Принцип Даламбера для материальной точки и механической системы. Уравнения метода кинетостатикиДифференциальные уравнения поступательного движения, вращательного и Плоскопараллельного движения твердого тела. Дифференциальные уравнения поступательного движения Изучение кинематики поступательного движения АТТ показало, что исследование поступательного движения АТТ сводится к рассмотрению движения любой ее МТ. Взяв в качестве такой МТ центр масс С, на основании теоремы о движении центра масс можно записать дифференциальные уравнения поступательного движения АТТ в виде:
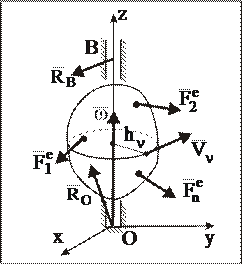
При движении центра масс АТТ в одной плоскости, например xOy, дифференциальные уравнения поступательного движения АТТ будут представлены двумя первыми уравнениями из соотношений (1). Дифференциальное уравнение вращательного движения АТТ относительно неподвижной оси Пусть на АТТ, имеющую неподвижную ось вращения z и оси х и у жестко связанных с АТТ, действует система внешних сил Чтобы получить дифференциальное уравнение вращательного движения АТТ относительно неподвижной оси Оz, применим теорему об изменении кинетического момента МС относительно оси вращения Oz:
Рис. 1 Так как реакции
и, следовательно,
Найдем кинетический момент АТТ, вращающейся относительно неподвижной оси Оz (рис2)
Скорость n-й точки АТТ, вращающейся относительно неподвижной оси, определится соотношением:
где w – угловая скорость АТТ, а hn – расстояние от n-й точки АТТ до оси z. Момент количества движения n-й МТ относительно оси Oz примет вид:
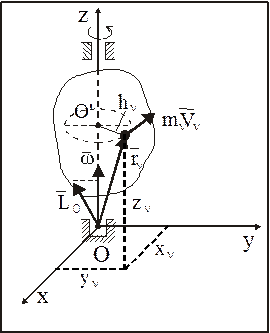
рис2 Тогда кинетический момент АТТ относительно неподвижной оси определится из соотношения:
здесь Окончательно для кинетического момента АТТ, вращающейся относительно неподвижной оси, имеем:
Подставляя в уравнение (2) найденное значение кинетического момента АТТ, получим:
Для АТТ момент инерции JОz = const и, следовательно,
Уравнения (3) представляют собой различные формы записи уравнения вращательного движения АТТ вокруг неподвижной оси. На основании третьего соотношения (3) можно сделать вывод, что при данном значении вращательного момента
Дифференциальные уравнения плоскопараллельного движения АТТ Предположим, что АТТ под действием системы внешних сил
Рис. 3 Из кинематики известно, что для определения положения АТТ, совершающего плоскопараллельное движение, достаточно задать положение какой-нибудь его МТ, принятой за полюс, и угол поворота АТТ вокруг оси, проходящей через этот полюс и перпендикулярной к неподвижной плоскости, параллельно которой происходит движение всех МТ рассматриваемого АТТ. Задачи динамики решаются проще, если за полюс взять центр масс С и определять положение АТТ координатами Таким образом, для изучения плоскопараллельного движения свободного АТТ достаточно составить три дифференциальных уравнения, связывающих величины
Замечание: без доказательства приняли, что уравнение вращения относительно подвижной оси Oz сохраняет свой вид, как для случая вращения относительно неподвижной оси. Принцип Даламбера для материальной точки и механической системы. Уравнения метода кинетостатики Основное уравнение динамики точки:
Получившееся дополнительное слагаемое имеет размерность силы и принимается за силу инерции, направленную в сторону противоположную ускорению:
С введением силы инерции уравнение динамики точки принимает вид уравнения равновесия:
Принцип Даламбера для материально точки: Геометрическая сумма приложенных к точке сил и силы инерции этой точки равна нулю. Для несвободной материально точки под Принцип Даламбера для несвободной механической системыполучим, записывая принцип Даламбера для каждой k-той точки и вводя реакции связей по аксиоме связей:
Здесь
На практике пользуются следствиями этих уравнений (принципа Даламбера). Сложим все N уравнений:
где
Следствие 1: Геометрическая сумма главных векторов задаваемых сил, реакций связи и сил инерции материальных точек равна нулю. Умножим каждое из N уравнений, выражающее принцип Даламбера системы на радиус-вектор, проведенный из центра O
Теперь сложим все N уравнений:
где
В результате получено Следствие 2: Геометрическая сумма главных моментов задаваемых сил, реакций связи и сил инерции материальных точек относительно любого центра равна нулю. Уравнения (5,6) называют обычно уравнениями метода кинетостатики.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1)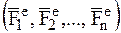 . Использовав принцип освобождаемости, заменим действие связей в подпятнике О и подшипнике В силами реакции связи
. Использовав принцип освобождаемости, заменим действие связей в подпятнике О и подшипнике В силами реакции связи 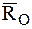 и
и 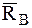 (рис1).
(рис1).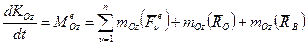 .
.
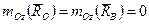
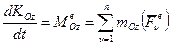 . (2)
. (2)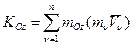 .
.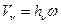 ,
,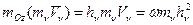 .
.
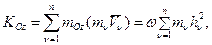
 – момент инерции АТТ относительно оси Oz.
– момент инерции АТТ относительно оси Oz.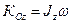 .
.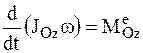 .
.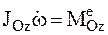 ,
, 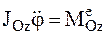 ,
, 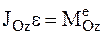 . (3)
. (3)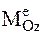 , чем больше
, чем больше 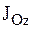 – момент инерции АТТ относительно оси вращения, тем меньше e – угловое ускорение АТТ и наоборот. Следовательно, момент инерции
– момент инерции АТТ относительно оси вращения, тем меньше e – угловое ускорение АТТ и наоборот. Следовательно, момент инерции 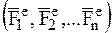 совершает плоскопараллельное движение, при котором все точки АТТ движутся в плоскостях, параллельных некоторой неподвижной плоскости, в качестве которой примем координатную плоскость xOy (рис. 3).
совершает плоскопараллельное движение, при котором все точки АТТ движутся в плоскостях, параллельных некоторой неподвижной плоскости, в качестве которой примем координатную плоскость xOy (рис. 3).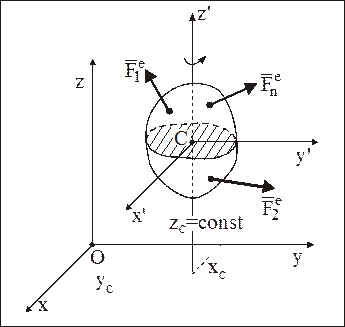
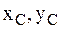 центра масс и углом поворота j АТТ вокруг оси
центра масс и углом поворота j АТТ вокруг оси 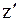 , проходящей через центр масс С и перпендикулярной к плоскости xOy.
, проходящей через центр масс С и перпендикулярной к плоскости xOy.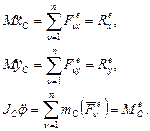 (4)
(4)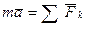 (1)
(1) Перенесем произведение массы на ускорение в правую часть:
Перенесем произведение массы на ускорение в правую часть: 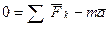
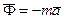 (2)
(2)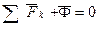 (3)
(3)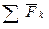 следует понимать не только активные силы, но и реакции связей (в соответствии с аксиомой связей).Сила инерции условно добавляется к действующим на точку силам, образуя взаимно уравновешенную систему сил.
следует понимать не только активные силы, но и реакции связей (в соответствии с аксиомой связей).Сила инерции условно добавляется к действующим на точку силам, образуя взаимно уравновешенную систему сил.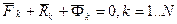 (4)
(4)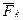 – равнодействующая задаваемых сил, приложенных к точке,
– равнодействующая задаваемых сил, приложенных к точке,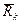 – равнодействующая реакций связей, приложенных к точке,
– равнодействующая реакций связей, приложенных к точке, 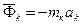 – сила инерции точки.
– сила инерции точки.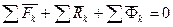 или
или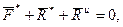 (5)
(5)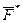 – главный вектор задаваемых сил, приложенных к точке,
– главный вектор задаваемых сил, приложенных к точке, – главный вектор реакций связей, приложенных к точке,
– главный вектор реакций связей, приложенных к точке, 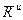 – главный вектор сил инерции точек системы. Таким образом, получено
– главный вектор сил инерции точек системы. Таким образом, получено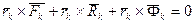 .
.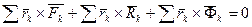 или
или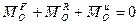 , (6)
, (6)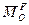 – главный момент задаваемых сил относительно центра O,
– главный момент задаваемых сил относительно центра O,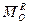 – главный момент реакций связей относительно центра O,
– главный момент реакций связей относительно центра O,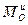 – главный момент сил инерции точек системы относительно центра O.
– главный момент сил инерции точек системы относительно центра O.