
|
|
Малые свободные колебания механических систем с двумя степенями свободы. Главные колебания.Из уравнений движения консервативной механической системы около устойчивого положения равновесия
в случае двух степеней свободы имеем:
(Согласно критерию Сильвестра:
(1) система дифференциальных уравнений малых свободных колебаний механической системы с двумя степенями свободы около устойчивого положения равновесия. Ее решение ищется в виде:
Подстановка этого решения в систему дифференциальных уравнений малых колебаний дает:
Относительно A и B это система однородных алгебраических уравнений. Она имеет нетривиальное решение, когда определитель системы равен нулю:
или
Это биквадратное уравнение называется уравнением частот, оно имеет два положительных корня
Таким образом, каждая обобщенная координата находится как сумма двух колебаний разной частоты, которые называются главными колебанииями. При этом, как следует из системы (3), амплитуды главных колебаний связаны между собой следующим образом:
где В итоге решение уравнений свободных колебаний (1) окончательно принимает вид:
Входящие в(6) амплитуды
Вынужденные колебания механических систем с двумя степенями свободы. Динамический гаситель колебаний Исключение нежелательных колебаний в механических системах называется виброзащитой (демпфированием).Используемые при этом технические устройства называются виброгасителями (демпферами). Принцип работы динамического гасителя основан на использовании явления антирезонанса, когда действие периодически изменяющейся возмущающей обобщенной силы соответствующей одной координате, нейтрализуется действием потенциальной обобщенной силы, соответствующей другой координате. Пусть к механической системе помимо консервативных сил приложена возмущающая сила, которая изменяется с течением времени по гармоническому закону
Дифференциальные уравнения движения механической системы в этом случае имеют вид:
Общее решение системы линейных дифференциальных неоднородных( в данном случае) уравнений ищем как сумму двух решений: С учетом зависимости возмущающей силы от времени частное решение ищется в виде
Подстановка его в систему дифференциальных уравнений дает:
Решая эту систему по правилу Крамера, получим
Поскольку при совпадении частоты возмущающей силы с одной из частот собственных колебаний Общее решение системы дифференциальных уравнений вынужденных колебаний при
Как видно, за счет выбора параметров колеблющейся системы можно добиться, например, выполнения условия А =0, т. е. амплитуда вынужденных колебаний, соответствующих первой обобщенной координате, обращается в ноль. Такое явление и называется антирезонансом. В рассматриваемом случае это имеет место, если
Основные понятия и гипотезы теории удара. Основное уравнение теории удара Явление, при котором за малый промежуток времени, т.е. почти мгновенно, скорости точек материальных объектов изменяются на конечные величины, называется ударом. Так как при ударе конечное изменение скоростей происходит за весьма малый промежуток времени, то при этом возникают очень большие ускорения, а, следовательно, и очень большие силы. Эти силы действуют в течение весьма малого промежутка времени, но их импульсы за этот промежуток времени являются конечными величинами. Силы, возникающие при ударе в течение малого промежутка времени, но достигающие при этом большой величины, так что их импульсы за этот промежуток времени являются конечными величинами, называются ударными силами. Малый промежуток времени, в течение которого длится удар, называется временем удара. Импульсы ударных сил за время удара называются ударными импульсами. Пусть дана МТ массы m, которая движется под действием обычной (неударной) силы Применяя теорему об изменении количества движения точки, получим:
где По теореме о среднем значении определенного интеграла можно написать:
где Итак, импульсами неударных сил за время удара будем пренебрегать по сравнению с импульсами ударных сил. Окончательно получим:
В рассматриваемой элементарной теории удара (1) принимается в качестве основного уравнения: Изменение количества движения МТ за время удара равно действующему на эту МТ ударному импульсу. (1) играет такую же роль в теории удара, как второй закон динамики при изучении движений под действием обычных сил. Проектируя векторное равенство (1) на координатные оси, получим три следующих уравнения:
Определим перемещение точки за время удара. Так как
Проинтегрировав это равенство в пределах от
Таким образом, перемещением МТ за время удара можно пренебречь

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
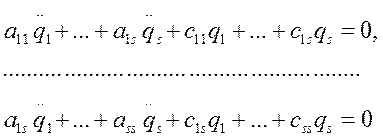
 (1)
(1)
 (2)
(2) (3)
(3)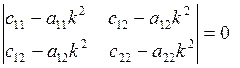
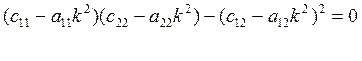 (4)
(4)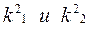 , которым соответствуют два решения системы дифференциальных уравнений малых колебаний:
, которым соответствуют два решения системы дифференциальных уравнений малых колебаний: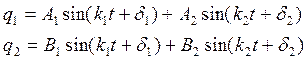
 (5)
(5) — коэффициенты формы главных колебаний.
— коэффициенты формы главных колебаний. (6)
(6) ,
,  и начальные фазы
и начальные фазы  ,
,  колебаний определяются из начальных условий.
колебаний определяются из начальных условий.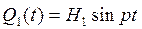
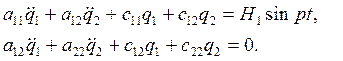
 ,— общее решение системы однородных дифференциальных уравнений;
,— общее решение системы однородных дифференциальных уравнений;  —частное решение системы неоднородных дифференциальных уравнений.
—частное решение системы неоднородных дифференциальных уравнений.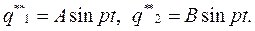
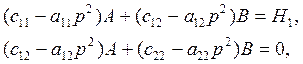
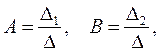
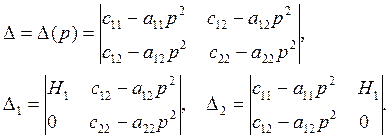
 совпадает с левой частью уравнения частот и обращается в ноль
совпадает с левой частью уравнения частот и обращается в ноль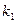 или
или  Коэффициенты A и B при этом обращаются в бесконечность. Таким образом, в случае колебаний системы с двумя степенями свободы существуют две резонансные частоты
Коэффициенты A и B при этом обращаются в бесконечность. Таким образом, в случае колебаний системы с двумя степенями свободы существуют две резонансные частоты 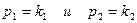
 имеет вид:
имеет вид: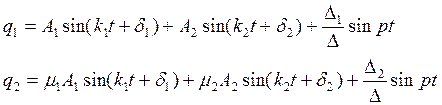

 . В момент
. В момент  , когда рассматриваемая МТ имеет скорость
, когда рассматриваемая МТ имеет скорость 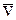 – скорость до удара, на нее начинает действовать ударная сила
– скорость до удара, на нее начинает действовать ударная сила  , действие которой прекращается в момент
, действие которой прекращается в момент  . Определим движение МТ под действием сил
. Определим движение МТ под действием сил  .
. ,
, – скорость точки в момент
– скорость точки в момент  ,
, и
и  есть средние значения сил
есть средние значения сил  ). Поэтому произведение
). Поэтому произведение  будет пренебрежимо мало по сравнению с произведением
будет пренебрежимо мало по сравнению с произведением  , являющимся величиной конечной.
, являющимся величиной конечной. . (1)
. (1) (2)
(2) , где
, где  – радиус-вектор, определяющий положение данной МТ относительно некоторой системы отсчета, то уравнение (1) можно записать следующим образом:
– радиус-вектор, определяющий положение данной МТ относительно некоторой системы отсчета, то уравнение (1) можно записать следующим образом: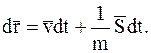
 ,
, есть среднее значение ударного импульса за время удара
есть среднее значение ударного импульса за время удара  - весьма мало, приходим к выводу, что
- весьма мало, приходим к выводу, что  будет близко к нулю и, следовательно, за время удара перемещение МТ
будет близко к нулю и, следовательно, за время удара перемещение МТ  практически равно нулю.
практически равно нулю.