
|
|
Эмпирическая функция распределенияЭмпирической функцией выборки (функцией распределения выборки) называется функция
, которую можно записать в следующем виде:
Данная функция непрерывная, кусочно-постоянна и изменяется в каждой точке хi, где хi — варианта рассматриваемого статистического распределения.
Пример По заданной выборке построить эмпирическую функцию выборки.
Коэффициент корреляции и его свойства Термин "корреляция" означает "связь". Если распределение переменных нормальное или несущественно отличается от нормального, применяют коэффициент корреляции Пирсона. Для порядковых (ранговых) переменных или переменных, чье распределение существенно отличается от нормального, используется коэффициент корреляции Спирмана или Кендалла. Имейте в виду, существуют и другие коэффициенты. Коэффициент корреляции Пирсонабудем обозначать cor(x,y), он рассчитывается по формуле:
где xi ,yi наблюдения, элементы выборки, Начнем с того, что напомним математические свойства коэффициента корреляции, который где x и y – изучаемые переменные. 1. 2. Если x и y независимые переменные, то 3. Если x и y связаны линейной зависимостью, то есть найдутся a и b такие, что 4. Если 5. Неверно, что если 6. Величина коэффициента корреляции не изменится, если ко всем значениям переменной добавить одно и то же число, или если все значения переменной умножить на одно и то же число, отличное от нуля. Такое свойство называется инвариантностью относительно сдвига и масштаба. Коэффициент корреляции – безразмерная величина, то есть не зависит от единиц, в которых измерены переменные. На практике коэффициент корреляции используется как некоторый «градусник», который показывает «ноль» в случае независимости переменных (смотри свойства 1 и 5), плюс единицу в случае прямой линейной зависимости переменных и минус единицу в случае обратной линейной зависимости переменных (смотри свойства 3 и 4). Значения коэффициента, находящиеся между нулем и единицей понимаются (с математической точки зрения необосновано!) так: чем ближе значение коэффициента корреляции к нулю, тем слабее зависимость, чем ближе к (плюс или минус) единице – тем сильнее зависимость. Отметим, что речь идет лишь об интерпретации свойств коэффициента корреляции, при этом аналитик далеко выходит за рамки математически точных утверждений. Таблица(по модулю)
Экзаменационный билет № 15 Полигон и гистограмма Полигоном частот (относительных частот) называется ломаная линия с вершинами в точках (xk , nk), где xk – варианта, nk – ее частота, или (xk , Wk), где Wk - относительная частота. Для непрерывных распределений более наглядное представление о характере распределения случайной величины дает гистограмма. Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников с основаниями длиной h и высотой ni/h, где h - длина каждого частичного интервала. Если соединить середины верхних прямоугольников гистограммы, то получим полигон частот. Полигон (для дискретной случайной величины) - ломаная, соединяющая точки (хi, ni — полигон Полигон частот:
Гистограмма — ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются отрезки длиной xi-xi-1, а их высоты равны:
Если объем выборки из генеральной совокупности случайной непрерывной величины велик, то прибегают к предварительной группировке данных: размах выборки разбивают на k частичных интервалов Ji. Количество интервалов подсчитывается по формуле: k=log2n+1 Подсчитывается, сколько значений из n1, n2,...,nm попало в каждый из к интервалов. Вариантами для выборки считают середины этих интервалов. Эмпирической плотностью распределения выборки:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
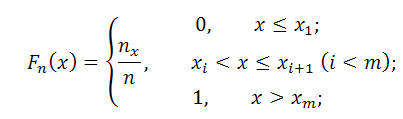

 , (1)
, (1) - средние значения, n – число наблюдений. Заметим, что формула (1) задает эмпирическую версию коэффициента, которая является оценкой теоретического значения.
- средние значения, n – число наблюдений. Заметим, что формула (1) задает эмпирическую версию коэффициента, которая является оценкой теоретического значения.
 .
.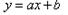 , то
, то  . При этом знак в правой части последнего равенства совпадает со знаком a.
. При этом знак в правой части последнего равенства совпадает со знаком a. , то x и y связаны линейной зависимостью, то есть найдутся a и b такие, что
, то x и y связаны линейной зависимостью, то есть найдутся a и b такие, что  . При этом знак в правой части последнего равенства совпадает со знаком a.
. При этом знак в правой части последнего равенства совпадает со знаком a. , то переменные x и y независимы. Важным исключением является случай, когда переменные x и y имеют нормальное распределение.
, то переменные x и y независимы. Важным исключением является случай, когда переменные x и y имеют нормальное распределение.

