
|
|
Термодинамические потенциалыЛюбая термодинамическая система стремится к фазовому равновесию как к состоянию с наименьшей энергией. Необходимым условием равновесия является неизменность параметров системы (плотности, давления, температуры, и т. д.) с течением времени (стационарное состояние) и отсутствие в системе постоянных потоков (теплоты, вещества, и т. п.). Термодинамическое равновесие системы характеризуется термодинамическими потенциалами. Все термодинамические параметры системы − давление p, объем V, температура T, и др. − могут быть получены как частные производные термодинамических потенциалов. Основное уравнение термодинамики для равновесных процессов
где U – внутренняя энергия системы, S – ее энтропия. Основное уравнение термодинамики связывает пять физических величин: температуру, давление, объем, энтропию и внутреннюю энергию (T, p, V, S, U). Для каждой пары из них существует термодинамический потенциал. Если за независимые переменные в уравнении (1) принять энтропию и объем (S и V), то для определения остальных величин необходимо задать зависимость внутренней энергии от энтропии и объема. Перепишем (1) как
где индексы V и S означают, что система находится при постоянных объеме и энтропии соответственно. Значит, для независимых переменных S и V внутренняя энергия U является термодинамическим потенциалом. Рассмотрим другие варианты. Пусть независимыми переменными являются температура (T) и объем (V). Термодинамическим потенциалом в этом случае служит свободная энергия Гельмгольца F:
Для независимых переменных T и p термодинамическим потенциалом является энергия Гиббса G:
Энтальпия На практике наиболее удобными являются потенциалы Гиббса и Гельмгольца, поскольку переменные объем-температура (V, T) и давление-температура (p, T) могут быть экспериментально измерены. Часто в реальных термодинамических системах приходится иметь дело с переменным числом частиц. Внутренняя энергия такой системы может меняться за счет изменения числа частиц какого-либо сорта i на величину
Величина Для систем с переменным числом частиц в выражения для дифференциалов свободной энергии и потенциала Гиббса также будет входить дополнительный член
Все термодинамические потенциалы являются экстенсивными величинами, т. е. они пропорциональны количеству вещества. Величины, не зависящие от количества вещества, называются интенсивными, к ним, например, относятся плотность, концентрация, температура. Экстенсивные величины выражаются математически однородными функциями, и для них справедлива теорема Эйлера об однородных функциях
где
Дальнейшие рассуждения будут базироваться на понятиях термодинамических потенциалов, введенных выше.
Влажный воздух Влажный воздух – это смесь сухого воздуха и водяного пара. В воздухе при определенных условиях кроме водяного пара может находиться его жидкая (вода) или кристаллическая (лед, снег) фаза. В естественных условиях воздух всегда содержит водяной пар. Влажный воздух можно рассматривать как смесь сухого воздуха и водяного пара (жидкую и твердую фазы воды в воздухе пока считаем отсутствующими). Используя законы для смесей газов, получим, что давление влажного воздуха равно сумме парциальных давлений сухого воздуха и водяного пара: Р = Рв + Рп . (7.1) Для наглядности представления основных характеристик влажного воздуха изобразим в Р,v- диаграмме (рис.7.1) состояния водяного пара во влажном воздухе. В качестве определяющих параметров водяного пара во влажном воздухе используются температура воздуха
t и парциальное давление водяного пара Рп. Водяной пар во влажном воздухе может находиться в трех состояниях (рис.7.1): точка 1 – перегретый пар, точка 2 – сухой насыщенный пар, точка 3 – влажный насыщенный пар (сухой насыщенный пар плюс капельки жидкости в состоянии насыщения). Высшим пределом парциального давления водяных паров при данной температуре воздуха t является давление насыщения пара Рп max = Рн. Абсолютная влажность r– это массовое количество водяных паров в одном кубическом метре влажного воздуха. Для ее определения используется величина, обратная удельному объему водяного пара при Рп и t, r=1/v (кг/м3). Действительно, по закону Дальтона водяной пар занимает весь объем смеси, а его плотность соответствует массе водяного пара в одном кубическом метре влажного воздуха. Необходимо отметить, что абсолютная влажность воздуха характеризует содержание в воздухе только одной – паровой фазы воды. Относительная влажность j– это отношение абсолютной влажности к максимально возможной влажности воздуха при данной температуре:
где r" и v"–максимальная абсолютная влажность воздуха и удельный объем сухого насыщенного водяного пара при данной температуре t. Относительная влажность воздуха характеризует потенциальную возможность воздуха испарять влагу и забирать в себя пар из окружающей среды при данной температуре. Максимальное содержание пара в воздухе соответствует состоянию точки 2 в Р,v- диаграмме (см. рис.7.1), где пар сухой насыщенный. При переходе в область влажного пара при данной температуре t (точка 3) в воздухе количество сухого насыщенного пара остается постоянным (такое же, как в точке 2) (для паровой фазы воды в этом случае удельный объем остается неизменным, v"=const, и минимально возможным при данной температуре воздуха), только к нему добавляются капельки воды в состоянии насыщения. Различают 3 состояния влажного воздуха. 1.Ненасыщенный влажный воздух – j<100 %, Рп<Рн, r<r", водяной пар во влажном воздухе в виде перегретого пара (точка 1). 2.Насыщенный влажный воздух – j=100 %, Рп=Рн, r=r", водяной пар во влажном воздухе в виде сухого насыщенного пара (точка 2). 3.Перенасыщенный влажный воздух– j=100 %, Рп=Рн, r=r", кроме сухого насыщенного пара в воздухе находятся капельки воды в состоянии насыщения или льда, снега (точка 3 при наличии капелек воды). В технике используется такая характеристика влажного воздуха, как температураточки росы. Это такая температура, начиная с которой при охлаждении влажного воздуха при постоянном давлении из него начинается выпадение капелек воды (соответствует температуре точки А процесса 1А, рис. 7.1). При снижении температуры воздуха ниже температуры точки росы при постоянном давлении всей смеси и постоянном содержании в ней H2О (процесс АВ) парциальное давление водяного пара уменьшается (Рвп<Рп), количество сухого насыщенного пара уменьшается, а количество капелек воды увеличивается. В этом случае в P,v- диаграмме процесс АВ пойдет в области влажного пара с уменьшением степени сухости по мере снижения температуры. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , отсюда dU является полным дифференциалом, и остальные параметры (температура и давление) можно определить как:
, отсюда dU является полным дифференциалом, и остальные параметры (температура и давление) можно определить как: ;
;  ,
,
 ;
;
 ;
;
 ;
;  .
.
 ;
;
 ;
;
 ;
;  .
.
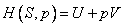 , также один из термодинамических потенциалов.
, также один из термодинамических потенциалов.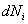 . Тогда основное уравнение термодинамики для таких систем принимает вид
. Тогда основное уравнение термодинамики для таких систем принимает вид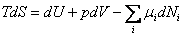 ;
;
 .
.
 называется химическим потенциалом i-го сорта частиц и имеет смысл энергии, приходящейся на одну частицу.
называется химическим потенциалом i-го сорта частиц и имеет смысл энергии, приходящейся на одну частицу. . Следовательно, химический потенциал
. Следовательно, химический потенциал  можно получить дифференцированием любого из термодинамических потенциалов по числу частиц
можно получить дифференцированием любого из термодинамических потенциалов по числу частиц .
.
 ,
,
 − экстенсивная величина. Применяя эту теорему к термодинамическому потенциалу Гиббса, получим
− экстенсивная величина. Применяя эту теорему к термодинамическому потенциалу Гиббса, получим .
.
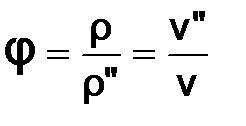 , (7.2)
, (7.2)