|
Сопротивлений витка с переменным током на проводящем полупространстве
Для примера на рис. 3.15 приведен годограф, в относительных величинах описывающий изменение импеданса витка с переменным током, расположенного на поверхности немагнитного проводящего полупространства, при изменении обобщенного параметра  . Причем годограф будет одним и тем же, чем бы ни было вызвано увеличение . Причем годограф будет одним и тем же, чем бы ни было вызвано увеличение 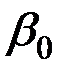 – увеличением частоты или электропроводности (это следует из выражения (3.59) для обобщенного параметра). – увеличением частоты или электропроводности (это следует из выражения (3.59) для обобщенного параметра).
Рис. 3.16. Годографы сигналов накладного параметрического ВТП при изменении параметра 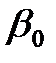 и зазоров между датчиком и изделием и зазоров между датчиком и изделием
Изменение числа витков параметрического ВТП не меняет вид годографа. На рис. 3.16 приведены годографы сигналов накладного параметрического ВТП, полученные при изменении параметра 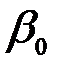 и зазоров между преобразователем и изделием. Сравнивая рис. 3.15 и 3.16, легко увидеть, что при отсутствии зазора ( и зазоров между преобразователем и изделием. Сравнивая рис. 3.15 и 3.16, легко увидеть, что при отсутствии зазора ( 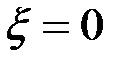 ) годографы витка и катушки совпадают. При фиксированных значениях ) годографы витка и катушки совпадают. При фиксированных значениях 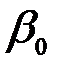 увеличение зазора приводит к уменьшению сигнала ВТП (красные пунктирные линии на рис. 3.16). Следует отметить, что линии изменения сигнала за счет увеличение зазора приводит к уменьшению сигнала ВТП (красные пунктирные линии на рис. 3.16). Следует отметить, что линии изменения сигнала за счет  и и  (синие линии) и линии (синие линии) и линии
изменения сигнала за счет зазора (красные пунктирные) имеют различные направления на комплексной плоскости ВТП и пересекаются под различными углами. Это обстоятельство может использоваться для разделения различных контролируемых параметров и подавления влияния мешающих параметров.
Анализируя годографы, выбирают оптимальную рабочую частоту, конструкцию датчика, измерительную схему и приемы контроля, обеспечивающие достаточную чувствительность прибора к проверяемому параметру, а также полную или частичную отстройку от влияния неконтролируемых параметров.
Основное влияние на вид годографов оказывает та часть вихревых токов, которая протекает вблизи измерительной обмотки ВТП. Поэтому годографы одностороннего ВТП (отраженное поле) и экранного ВТП (проходящее поле) при контроле одного и того же объекта существенно отличаются. В пределах каждой группы для всех типов преобразователей годографы 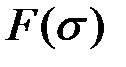 , , 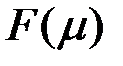 , , 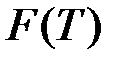 и другие близки по форме. Некоторая количественная разница между годографами для накладных, наружных и внутренних проходных ВТП объясняется тем, что та часть поля, в которую объект помещается для контроля, у этих датчиков не одинакова. и другие близки по форме. Некоторая количественная разница между годографами для накладных, наружных и внутренних проходных ВТП объясняется тем, что та часть поля, в которую объект помещается для контроля, у этих датчиков не одинакова.
Контроль цилиндрических объектов наружным проходным ВТП с однородным полем. Выбор наилучших условий контроля.
Размеры и электромагнитные параметры протяженных цилиндрических объектов кругового сечения, как однородных, так и многослойных, а также с изменяющимся сечением (например, с дефектом), целесообразно контролировать с помощью проходных преобразователей с однородным магнитным полем в зоне контроля. Однородное магнитное поле создают либо с помощью цилиндрической возбуждающей катушки с отношением длины к диаметру равным или больше четырех, либо используя две короткие возбуждающие катушки, выполненные в виде колец Гельмгольца (расстояние между катушками равно их радиусу). Внутренний диаметр короткой измерительной катушки должен быть близок к диаметру объекта контроля.
Рис. 3.17. Круговой цилиндр в проходном ВТП
Для определения оптимальных условий контроля кругового однородного цилиндра радиуса  с помощью наружного проходного ВТП, имеющего длинную возбуждающую катушку радиуса с помощью наружного проходного ВТП, имеющего длинную возбуждающую катушку радиуса 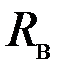 и создающего однородное переменное магнитное поле в зоне контроля (рис. 3.17), напряженность которого изменяется по синусоидальному закону и создающего однородное переменное магнитное поле в зоне контроля (рис. 3.17), напряженность которого изменяется по синусоидальному закону  , необходимо знать зависимость э. д. с. , необходимо знать зависимость э. д. с.  измерительной катушки ВТП от параметров контролируемого цилиндра. С этой целью находят или распределение напряженности магнитного поля измерительной катушки ВТП от параметров контролируемого цилиндра. С этой целью находят или распределение напряженности магнитного поля  и вычисляют магнитный поток и вычисляют магнитный поток 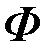 внутри цилиндра, или векторный потенциал внутри цилиндра, или векторный потенциал  в месте расположения витков измерительной катушки. в месте расположения витков измерительной катушки.
Магнитный поток внутри цилиндра определяется по формуле  , где , где 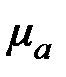 – абсолютная магнитная проницаемость материала цилиндра; – абсолютная магнитная проницаемость материала цилиндра; 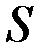 - площадь его поперечного сечения. - площадь его поперечного сечения.
В первом случае э. д. с. измерительной катушки определяется на основе закона электромагнитной индукции
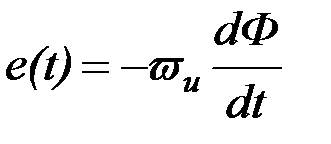 , (3.62) , (3.62)
где 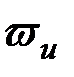 – количество витков измерительной катушки; – количество витков измерительной катушки; 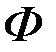 – магнитный поток, проходящий через эту катушку. – магнитный поток, проходящий через эту катушку.
Для синусоидального магнитного потока  комплексная амплитуда э. д. с. равна комплексная амплитуда э. д. с. равна
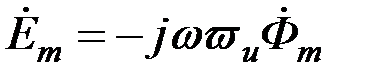 , (3.63) , (3.63)
где 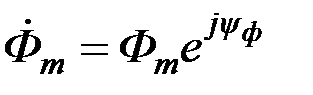 , , 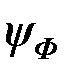 – начальная фаза магнитного потока. – начальная фаза магнитного потока.
Во втором случае комплексная амплитуда э. д. с. определяется через векторный потенциал 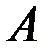 : :
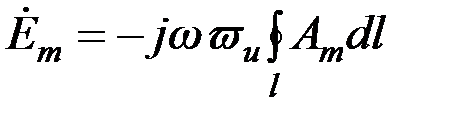 . (3.64) . (3.64)
Если круговая измерительная катушка радиусом 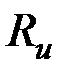 расположена коаксиально с круговым цилиндром, то расположена коаксиально с круговым цилиндром, то
 , (3.65) , (3.65)
где  – длина контура измерительной обмотки; – длина контура измерительной обмотки; 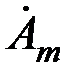 – комплексная амплитуда векторного потенциала. Индекс – комплексная амплитуда векторного потенциала. Индекс  часто опускают, так как можно пользоваться не только комплексными амплитудами, но и комплексными действующими значениями часто опускают, так как можно пользоваться не только комплексными амплитудами, но и комплексными действующими значениями 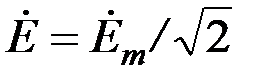 . Поэтому (3.65) можно записать в виде . Поэтому (3.65) можно записать в виде
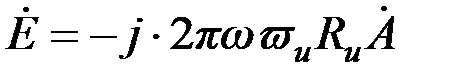 , (3.66) , (3.66)
или для напряжения
 (3.67) (3.67)
Для параметрических проходных ВТП комплексное[8] сопротивление можно определить по формуле
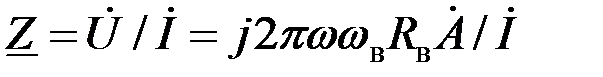 . (3.68) . (3.68)
Если параметры  и и  контролируемого цилиндра постоянные, а возбуждающее в нем вихревые токи электромагнитное поле монохроматическое, то, пренебрегая токами смещения, электромагнитное поле внутри цилиндра, где отсутствуют сторонние токи, можно описать однородными уравнениями Гельмгольца контролируемого цилиндра постоянные, а возбуждающее в нем вихревые токи электромагнитное поле монохроматическое, то, пренебрегая токами смещения, электромагнитное поле внутри цилиндра, где отсутствуют сторонние токи, можно описать однородными уравнениями Гельмгольца
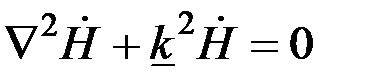 , (3.69) , (3.69)
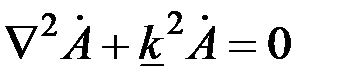 , (3.70) , (3.70)
где 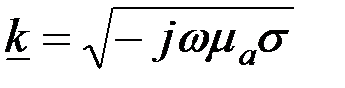 . Заметим, что . Заметим, что  , где , где 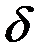 – глубина проникновения плоской электромагнитной волны в проводник. – глубина проникновения плоской электромагнитной волны в проводник.
Считая контролируемый цилиндр бесконечно длинным (на практике он значительно длиннее возбуждающей катушки), уравнения (3.69) и (3.70) в цилиндрических координатах   и и  можно представить уравнениями Бесселя: можно представить уравнениями Бесселя:
 , (3.71) , (3.71)
 . (3.72) . (3.72)
Для рассматриваемого случая, когда круговая возбуждающая катушка и контролируемый цилиндр коаксиальны, напряженность магнитного поля  имеет осевую имеет осевую 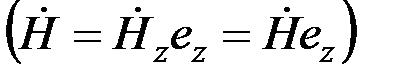 , а векторный потенциал , а векторный потенциал 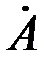 - угловую - угловую  составляющие, каждая из которых зависит только от составляющие, каждая из которых зависит только от  . В пространстве между возбуждающей катушкой и контролируемым цилиндром (при . В пространстве между возбуждающей катушкой и контролируемым цилиндром (при 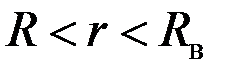 ) )  , так как магнитное поле ослабляется из-за действия вихревых токов только внутри цилиндра. Вне длинной возбуждающей катушки ( , так как магнитное поле ослабляется из-за действия вихревых токов только внутри цилиндра. Вне длинной возбуждающей катушки (  ) поле ) поле 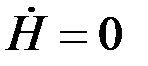 . .
Решение уравнений (3.71) и (3.72) получают, используя граничные условия (1.65) для 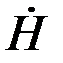 и и  на поверхности контролируемого цилиндра: на поверхности контролируемого цилиндра:
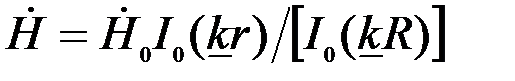 , (3.73) , (3.73)
 , (3.74) , (3.74)
где  и и 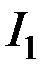 – модифицированные функции Бесселя первого рода соответственно нулевого и первого порядков. – модифицированные функции Бесселя первого рода соответственно нулевого и первого порядков.
Плотность вихревых токов в цилиндре
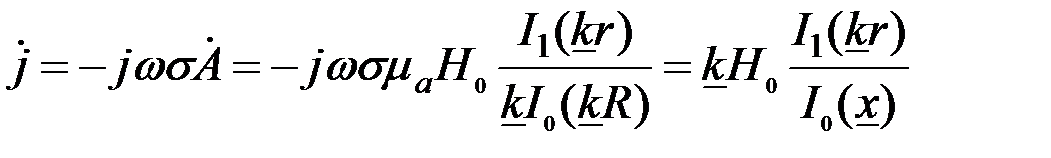 , (3.75) , (3.75)
где 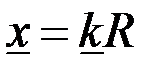 – обобщенный параметр контролируемого цилиндра. – обобщенный параметр контролируемого цилиндра.
Рис. 3.18. Распределение модулей относительной напряженности магнитного поля (а) и плотности вихревых токов (б) в круговом цилиндре
На рис. 3.18 приведены графики распределения модулей относительной напряженности магнитного поля  и относительной плотности вихревых токов и относительной плотности вихревых токов  , где , где  – модуль плотности вихревых токов на поверхности цилиндра. Уменьшение напряженности магнитного поля во внутренних слоях цилиндра обусловлено скин-эффектом. – модуль плотности вихревых токов на поверхности цилиндра. Уменьшение напряженности магнитного поля во внутренних слоях цилиндра обусловлено скин-эффектом.
В соответствии с правилом Ленца вторичное магнитное поле, создаваемое вихревыми токами, ослабляет первичное магнитное поле, причем во внутренних слоях цилиндра вторичное магнитное поле создается практически всеми вихревыми токами цилиндра, поэтому оно больше, чем в поверхностных слоях, где оно создается только токами более внешних слоев. Уменьшение плотности вихревых токов  во внутренних слоях цилиндра обусловлено уменьшением во внутренних слоях цилиндра обусловлено уменьшением 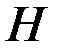 . Степень уменьшения . Степень уменьшения 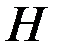 и и  зависит от модуля обобщенного параметра зависит от модуля обобщенного параметра  ; с ростом ; с ростом 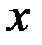 они уменьшаются быстрее. Из рис. 3.18б следует, что плотность вихревых токов на оси цилиндра равна нулю независимо от значения они уменьшаются быстрее. Из рис. 3.18б следует, что плотность вихревых токов на оси цилиндра равна нулю независимо от значения 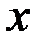 . .
Обобщенный параметр  связан с глубиной проникновения связан с глубиной проникновения  плоской электромагнитной волны в электропроводящую среду соотношением плоской электромагнитной волны в электропроводящую среду соотношением 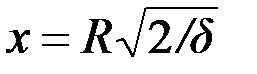 или или 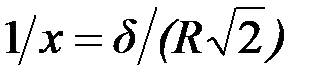 . .
Чтобы определить э. д. с. измерительной катушки по формуле (3.66), необходимо знать значения векторного потенциала 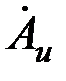 при при  (на поверхности цилиндра). Для этого используем соотношение (на поверхности цилиндра). Для этого используем соотношение 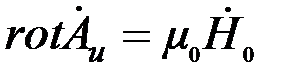 , справедливое при , справедливое при 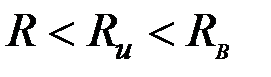 , которое в цилиндрических координатах имеет вид: , которое в цилиндрических координатах имеет вид:
 . (3.76) . (3.76)
Решением этого уравнения является функция:
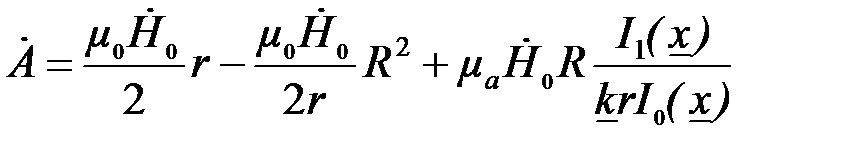 . (3.77) . (3.77)
Подставляя (3.77) в (3.66), получаем
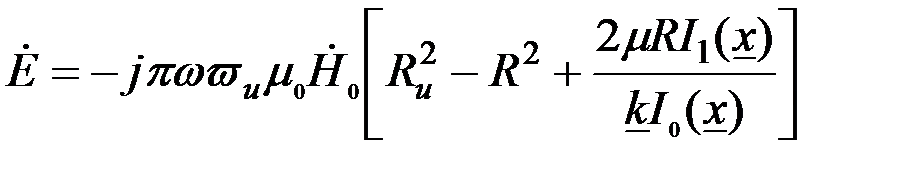 (3.78) (3.78)
При отсутствии электропроводящего цилиндра внутри проходного ВТП э. д. с. измерительной обмотки отлична от нуля и равна начальной э. д. с. ВТП
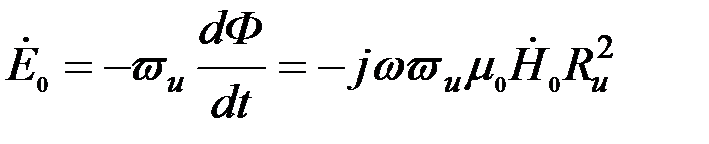 . (3.79) . (3.79)
Из (3.78) и (3.79) следует, что относительное напряжение измерительной обмотки равно
 , (3.80) , (3.80)
где 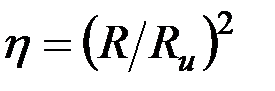 – коэффициент заполнения, равный отношению площади поперечного сечения контролируемого цилиндра к площади, охватываемой контуром измерительной обмотки, если ее радиус меньше радиуса возбуждающей катушки. При размещении измерительной обмотки поверх возбуждающей катушки, т.е. при – коэффициент заполнения, равный отношению площади поперечного сечения контролируемого цилиндра к площади, охватываемой контуром измерительной обмотки, если ее радиус меньше радиуса возбуждающей катушки. При размещении измерительной обмотки поверх возбуждающей катушки, т.е. при 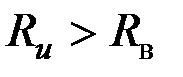 , коэффициент заполнения равен , коэффициент заполнения равен 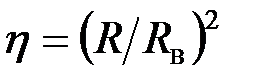 , поскольку поле вне возбуждающей катушки не влияет на вихревые токи в ОК. Таким образом, , поскольку поле вне возбуждающей катушки не влияет на вихревые токи в ОК. Таким образом,
 при при 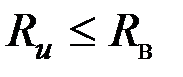 или или 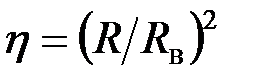 при при 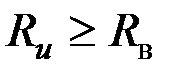 . (3.81) . (3.81)
В случае неферромагнитного цилиндра уменьшение магнитного потока за счет вихревых токов принято характеризовать эффективной магнитной проницаемостью – безразмерной комплексной величиной
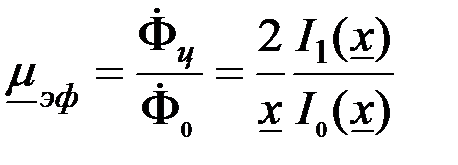 . (3.82) . (3.82)
где 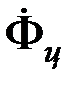 – магнитный поток, пронизывающий цилиндр при данном значении – магнитный поток, пронизывающий цилиндр при данном значении  ; ; 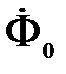 – магнитный поток через то же сечение при отсутствии цилиндра. Из определения и выражения (3.82) очевидно, что эффективная магнитная проницаемость не эквивалентна магнитной проницаемости – магнитный поток через то же сечение при отсутствии цилиндра. Из определения и выражения (3.82) очевидно, что эффективная магнитная проницаемость не эквивалентна магнитной проницаемости  , характеризующей интенсивность намагничивания ферромагнетика, и эти понятия следует разделять. , характеризующей интенсивность намагничивания ферромагнетика, и эти понятия следует разделять.
Подставляя выражение 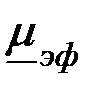 в (3.80), получаем в (3.80), получаем
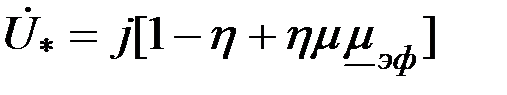 . (3.83) . (3.83)
При 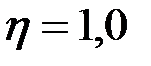 (т.е. при (т.е. при 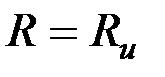 ) для ферромагнитного цилиндра следует ) для ферромагнитного цилиндра следует 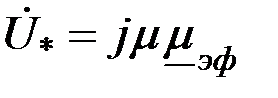 , а для неферромагнитных цилиндров (т.е. , а для неферромагнитных цилиндров (т.е. 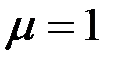 ) следует ) следует  . График . График 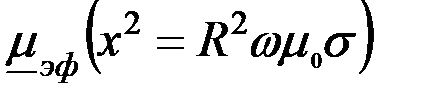 приведен на рис. 3.19. приведен на рис. 3.19.
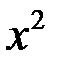 х2 х2
|
Рис. 3.19. Зависимость  от квадрата обобщенного параметра от квадрата обобщенного параметра 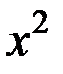
Рис. 3.20. Годографы относительного напряжения 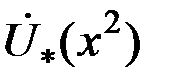 наружного проходного ВТП при контроле кругового неферромагнитного цилиндра наружного проходного ВТП при контроле кругового неферромагнитного цилиндра
На рис. 3.20 приведены годографы (годограф – геометрическое место концов векторов) относительного напряжения 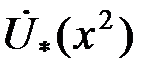 наружного проходного ВТП для проводящего немагнитного ( наружного проходного ВТП для проводящего немагнитного ( 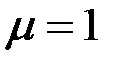 ) цилиндра при ) цилиндра при 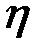 = 0,5; 0,75; 1,0 и = 0,5; 0,75; 1,0 и 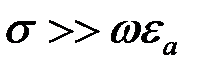 , т.е. когда плотность вихревых токов значительно больше плотности токов смещения. Основной годограф (при , т.е. когда плотность вихревых токов значительно больше плотности токов смещения. Основной годограф (при 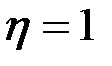 ) отличается от приведенного на рис. 3.19 лишь множителем ) отличается от приведенного на рис. 3.19 лишь множителем  , т.е. , т.е.  . Этот годограф показывает зависимость напряжения . Этот годограф показывает зависимость напряжения 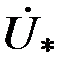 от удельной электрической проводимости от удельной электрической проводимости  при при  , так как , так как 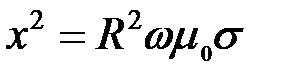 . .
Из (3.83) для 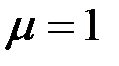 следует, что следует, что
 , (3.84) , (3.84)
т.е. годографы  – это прямые линии (красные сплошные на рис. 3.20). – это прямые линии (красные сплошные на рис. 3.20).
При изменении радиуса контролируемого цилиндра 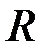 изменяются значения коэффициента заполнения изменяются значения коэффициента заполнения 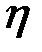 и обобщенного параметра и обобщенного параметра  , а следовательно, и величина , а следовательно, и величина 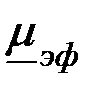 , поэтому годографы , поэтому годографы 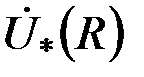 непрямолинейны (красные штриховые линии на рис. 3.20). непрямолинейны (красные штриховые линии на рис. 3.20).
Из рис. 3.20 следует, что при изменении параметра 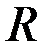 и и  контролируемого цилиндра годографы контролируемого цилиндра годографы  и и 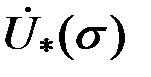 имеют различные направления, что позволяет раздельно контролировать указанные параметры цилиндра. Наилучшие условия раздельного контроля имеют различные направления, что позволяет раздельно контролировать указанные параметры цилиндра. Наилучшие условия раздельного контроля 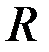 и и  существуют тогда, когда углы между годографами существуют тогда, когда углы между годографами 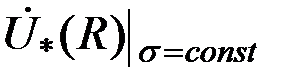 и и 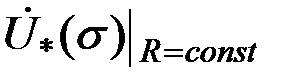 стремятся к стремятся к  . .
Особенность контроля ферромагнитных объектов состоит в сильном влиянии магнитных свойств объекта на годографы сигналов ВТП. С одной стороны, изменения магнитных свойств оказывают сильное мешающее влияние, затрудняя использование вихретоковых приборов, а с другой – именно благодаря структурной чувствительности магнитных свойств возможен контроль таких эксплуатационных характеристик, как твердость, механические напряжения, степень усталостного повреждения. Условия контроля ферромагнитных объектов отличаются от условий контроля неферромагнитных также и тем, что годографы сигналов ВТП существенно зависят от напряженности поля возбуждения. Нелинейность магнитных характеристик материалов ОК позволяет в качестве информативных параметров сигнала ВТП использовать высшие гармоники напряжения ВТП.
Рис. 3.21. Годографы относительного напряжения 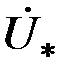 наружного проходного ВТП при изменении параметров ферромагнитного цилиндра для наружного проходного ВТП при изменении параметров ферромагнитного цилиндра для 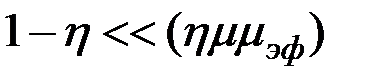
Проанализируем годографы сигнала ВТП в предположении линейности магнитных характеристик материала ОК, т.е. в предположении 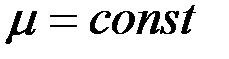 . Абсолютная магнитная проницаемость материала цилиндра . Абсолютная магнитная проницаемость материала цилиндра 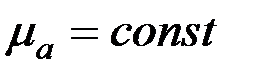 и при условии и при условии 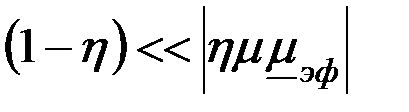 зависимости зависимости  имеют вид, показанный на рис. 3.21. Из рисунка видно, что при имеют вид, показанный на рис. 3.21. Из рисунка видно, что при 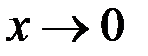 напряжение напряжение  в в  раз больше, чем при раз больше, чем при  . Это объясняется тем, что магнитный поток в ферромагнитном протяженном цилиндре, расположенном в однородном магнитном поле, в . Это объясняется тем, что магнитный поток в ферромагнитном протяженном цилиндре, расположенном в однородном магнитном поле, в 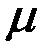 раз больше, чем в неферромагнитном. При раз больше, чем в неферромагнитном. При  напряжение напряжение 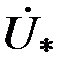 уменьшается в результате действия вихревых токов и при уменьшается в результате действия вихревых токов и при 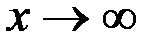 следует следует 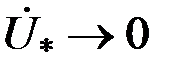 . Из рис. 3.21 видно, что направления изменения . Из рис. 3.21 видно, что направления изменения 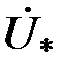 на комплексной плоскости при изменении на комплексной плоскости при изменении 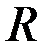 и и  совпадают. совпадают.
В практике вихретокового контроля начальное напряжение 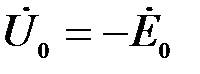 обычно компенсируют, поэтому за сигнал принимают относительное вносимое напряжение обычно компенсируют, поэтому за сигнал принимают относительное вносимое напряжение 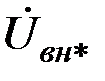 , возникающее при внесении контролируемого цилиндра в наружный проходной ВТП: , возникающее при внесении контролируемого цилиндра в наружный проходной ВТП:
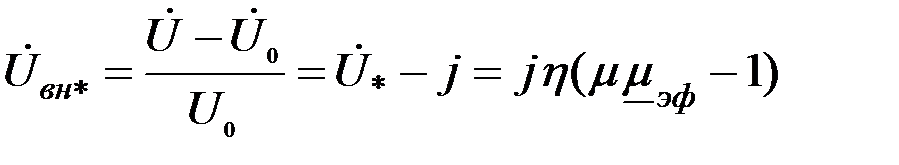 . (3.85) . (3.85)
Относительное вносимое напряжение 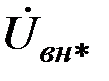 с увеличением с увеличением  монотонно возрастает от нуля до единицы. монотонно возрастает от нуля до единицы.
Чувствительности проходного ВТП. Чтобы создать оптимальные условия (режимы) для контроля какого-либо параметра цилиндрических объектов, необходимо знать чувствительность проходного ВТП к этому параметру. В теории вихретокового контроля используют понятие относительной комплексной чувствительности ВТП к контролируемому параметру  : :
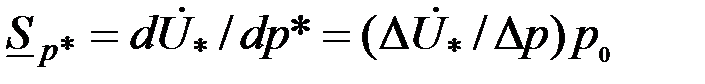 , (3.86) , (3.86)
где 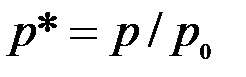 , , 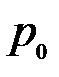 – номинальное значение параметра – номинальное значение параметра 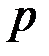 . .
Выражения для относительной комплексной чувствительности наружного проходного ВТП к изменениям 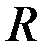 , ,  и и 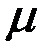 однородного кругового цилиндра при условии однородного кругового цилиндра при условии 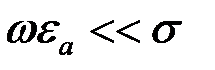 имеют вид имеют вид
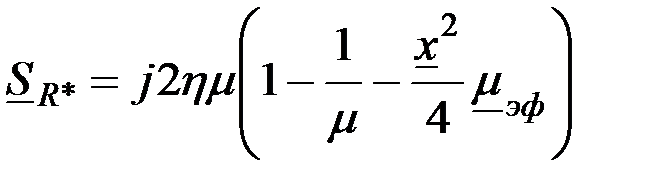 ; (3.87) ; (3.87)
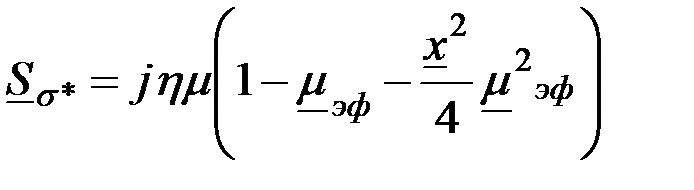 ; (3.88) ; (3.88)
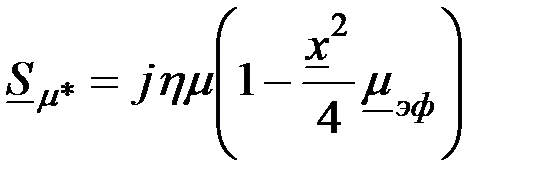 . (3.89) . (3.89)
На рис. 3.22а-в приведены годографы относительной комплексной чувствительности наружного проходного ВТП для  к изменению радиуса к изменению радиуса 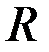 , удельной электрической проводимости , удельной электрической проводимости  (при (при  ) и магнитной проницаемости ) и магнитной проницаемости  (при (при 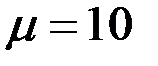 ). Направления векторов ). Направления векторов 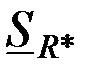 , , 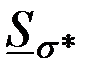 и и 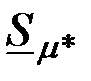 соответствуют направлениям касательных к соответствующим годографам рис. 3.20 для рассматриваемых значений соответствуют направлениям касательных к соответствующим годографам рис. 3.20 для рассматриваемых значений 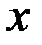 . На рис. 3.22 показаны векторы . На рис. 3.22 показаны векторы 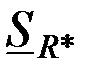 , , 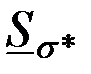 и и 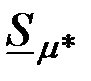 для для 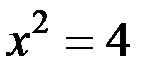 . Модули векторов рис. 3.22 пропорциональны приращениям . Модули векторов рис. 3.22 пропорциональны приращениям  , обусловленным изменением контролируемых параметров , обусловленным изменением контролируемых параметров  , ,  или или 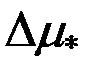 . .
На рис. 3.22г показаны зависимости модулей относительной чувствительности 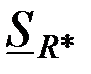 , , 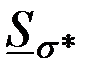 и и 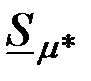 от от 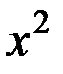 при тех же значениях коэффициента заполнения при тех же значениях коэффициента заполнения  и проницаемости и проницаемости 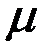 , что и годографы на рис. 3.22а-в. , что и годографы на рис. 3.22а-в.
Из рис. 3.22 видно, что с ростом 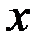 чувствительность чувствительность 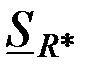 растет, стремясь к значению растет, стремясь к значению  ; ; 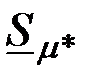 уменьшается до нуля при уменьшается до нуля при 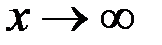 ; а чувствительность ; а чувствительность  вначале возрастает от нуля до вначале возрастает от нуля до 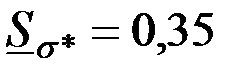 при при 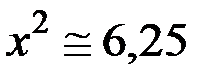 , а затем уменьшается, стремясь к нулю при , а затем уменьшается, стремясь к нулю при 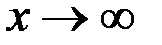 . .
Таким образом, наилучшие условия для контроля радиуса цилиндра соответствуют большим значениям  ; для контроля магнитной проницаемости – малым значениям ; для контроля магнитной проницаемости – малым значениям 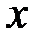 ; а для контроля удельной электрической проводимости – значению ; а для контроля удельной электрической проводимости – значению 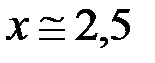 . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 . Причем годограф будет одним и тем же, чем бы ни было вызвано увеличение
. Причем годограф будет одним и тем же, чем бы ни было вызвано увеличение 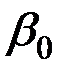 – увеличением частоты или электропроводности (это следует из выражения (3.59) для обобщенного параметра).
– увеличением частоты или электропроводности (это следует из выражения (3.59) для обобщенного параметра).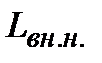

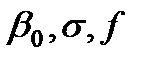
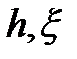
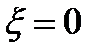
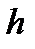
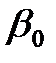 и зазоров между датчиком и изделием
и зазоров между датчиком и изделием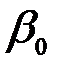 и зазоров между преобразователем и изделием. Сравнивая рис. 3.15 и 3.16, легко увидеть, что при отсутствии зазора (
и зазоров между преобразователем и изделием. Сравнивая рис. 3.15 и 3.16, легко увидеть, что при отсутствии зазора ( 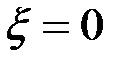 ) годографы витка и катушки совпадают. При фиксированных значениях
) годографы витка и катушки совпадают. При фиксированных значениях  и
и  (синие линии) и линии
(синие линии) и линии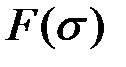 ,
, 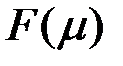 ,
, 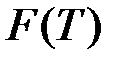 и другие близки по форме. Некоторая количественная разница между годографами для накладных, наружных и внутренних проходных ВТП объясняется тем, что та часть поля, в которую объект помещается для контроля, у этих датчиков не одинакова.
и другие близки по форме. Некоторая количественная разница между годографами для накладных, наружных и внутренних проходных ВТП объясняется тем, что та часть поля, в которую объект помещается для контроля, у этих датчиков не одинакова.

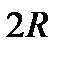

 с помощью наружного проходного ВТП, имеющего длинную возбуждающую катушку радиуса
с помощью наружного проходного ВТП, имеющего длинную возбуждающую катушку радиуса 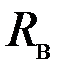 и создающего однородное переменное магнитное поле в зоне контроля (рис. 3.17), напряженность которого изменяется по синусоидальному закону
и создающего однородное переменное магнитное поле в зоне контроля (рис. 3.17), напряженность которого изменяется по синусоидальному закону  , необходимо знать зависимость э. д. с.
, необходимо знать зависимость э. д. с.  измерительной катушки ВТП от параметров контролируемого цилиндра. С этой целью находят или распределение напряженности магнитного поля
измерительной катушки ВТП от параметров контролируемого цилиндра. С этой целью находят или распределение напряженности магнитного поля  и вычисляют магнитный поток
и вычисляют магнитный поток 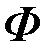 внутри цилиндра, или векторный потенциал
внутри цилиндра, или векторный потенциал  в месте расположения витков измерительной катушки.
в месте расположения витков измерительной катушки. , где
, где 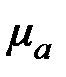 – абсолютная магнитная проницаемость материала цилиндра;
– абсолютная магнитная проницаемость материала цилиндра; 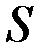 - площадь его поперечного сечения.
- площадь его поперечного сечения.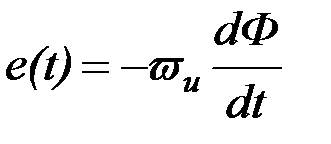 , (3.62)
, (3.62)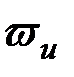 – количество витков измерительной катушки;
– количество витков измерительной катушки; 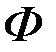 – магнитный поток, проходящий через эту катушку.
– магнитный поток, проходящий через эту катушку. комплексная амплитуда э. д. с. равна
комплексная амплитуда э. д. с. равна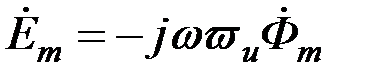 , (3.63)
, (3.63)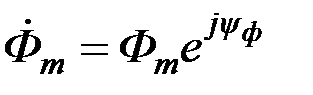 ,
, 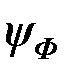 – начальная фаза магнитного потока.
– начальная фаза магнитного потока. :
: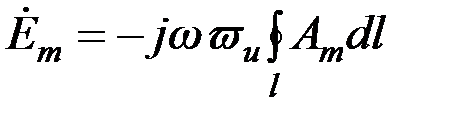 . (3.64)
. (3.64)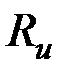 расположена коаксиально с круговым цилиндром, то
расположена коаксиально с круговым цилиндром, то , (3.65)
, (3.65) – длина контура измерительной обмотки;
– длина контура измерительной обмотки; 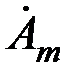 – комплексная амплитуда векторного потенциала. Индекс
– комплексная амплитуда векторного потенциала. Индекс  часто опускают, так как можно пользоваться не только комплексными амплитудами, но и комплексными действующими значениями
часто опускают, так как можно пользоваться не только комплексными амплитудами, но и комплексными действующими значениями 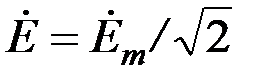 . Поэтому (3.65) можно записать в виде
. Поэтому (3.65) можно записать в виде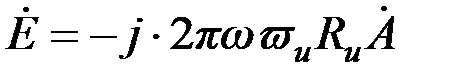 , (3.66)
, (3.66) (3.67)
(3.67)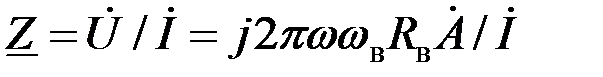 . (3.68)
. (3.68) и
и  контролируемого цилиндра постоянные, а возбуждающее в нем вихревые токи электромагнитное поле монохроматическое, то, пренебрегая токами смещения, электромагнитное поле внутри цилиндра, где отсутствуют сторонние токи, можно описать однородными уравнениями Гельмгольца
контролируемого цилиндра постоянные, а возбуждающее в нем вихревые токи электромагнитное поле монохроматическое, то, пренебрегая токами смещения, электромагнитное поле внутри цилиндра, где отсутствуют сторонние токи, можно описать однородными уравнениями Гельмгольца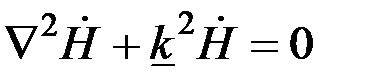 , (3.69)
, (3.69)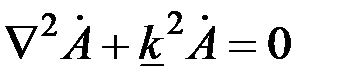 , (3.70)
, (3.70)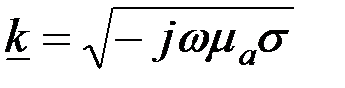 . Заметим, что
. Заметим, что  , где
, где 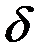 – глубина проникновения плоской электромагнитной волны в проводник.
– глубина проникновения плоской электромагнитной волны в проводник.
 и
и  можно представить уравнениями Бесселя:
можно представить уравнениями Бесселя: , (3.71)
, (3.71) . (3.72)
. (3.72) имеет осевую
имеет осевую 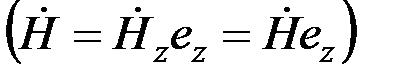 , а векторный потенциал
, а векторный потенциал 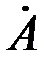 - угловую
- угловую  составляющие, каждая из которых зависит только от
составляющие, каждая из которых зависит только от  . В пространстве между возбуждающей катушкой и контролируемым цилиндром (при
. В пространстве между возбуждающей катушкой и контролируемым цилиндром (при 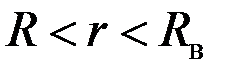 )
)  , так как магнитное поле ослабляется из-за действия вихревых токов только внутри цилиндра. Вне длинной возбуждающей катушки (
, так как магнитное поле ослабляется из-за действия вихревых токов только внутри цилиндра. Вне длинной возбуждающей катушки (  ) поле
) поле 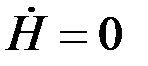 .
.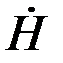 и
и  на поверхности контролируемого цилиндра:
на поверхности контролируемого цилиндра: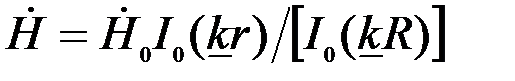 , (3.73)
, (3.73) , (3.74)
, (3.74) и
и 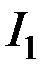 – модифицированные функции Бесселя первого рода соответственно нулевого и первого порядков.
– модифицированные функции Бесселя первого рода соответственно нулевого и первого порядков.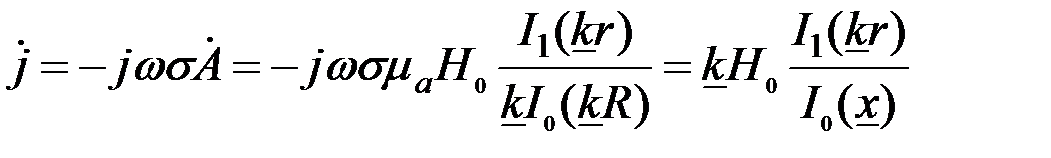 , (3.75)
, (3.75)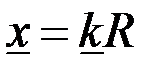 – обобщенный параметр контролируемого цилиндра.
– обобщенный параметр контролируемого цилиндра.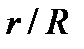
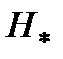


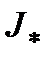

 и относительной плотности вихревых токов
и относительной плотности вихревых токов  , где
, где  – модуль плотности вихревых токов на поверхности цилиндра. Уменьшение напряженности магнитного поля во внутренних слоях цилиндра обусловлено скин-эффектом.
– модуль плотности вихревых токов на поверхности цилиндра. Уменьшение напряженности магнитного поля во внутренних слоях цилиндра обусловлено скин-эффектом. во внутренних слоях цилиндра обусловлено уменьшением
во внутренних слоях цилиндра обусловлено уменьшением 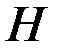 . Степень уменьшения
. Степень уменьшения 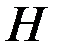 и
и  зависит от модуля обобщенного параметра
зависит от модуля обобщенного параметра  ; с ростом
; с ростом 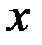 они уменьшаются быстрее. Из рис. 3.18б следует, что плотность вихревых токов на оси цилиндра равна нулю независимо от значения
они уменьшаются быстрее. Из рис. 3.18б следует, что плотность вихревых токов на оси цилиндра равна нулю независимо от значения 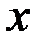 .
. связан с глубиной проникновения
связан с глубиной проникновения  плоской электромагнитной волны в электропроводящую среду соотношением
плоской электромагнитной волны в электропроводящую среду соотношением 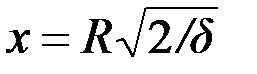 или
или 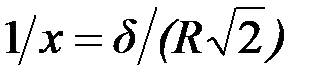 .
.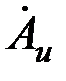 при
при  (на поверхности цилиндра). Для этого используем соотношение
(на поверхности цилиндра). Для этого используем соотношение 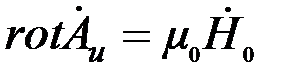 , справедливое при
, справедливое при 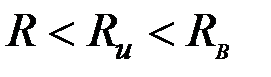 , которое в цилиндрических координатах имеет вид:
, которое в цилиндрических координатах имеет вид: . (3.76)
. (3.76)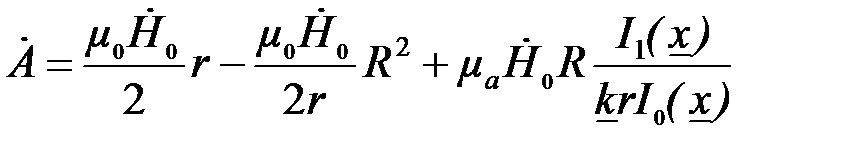 . (3.77)
. (3.77)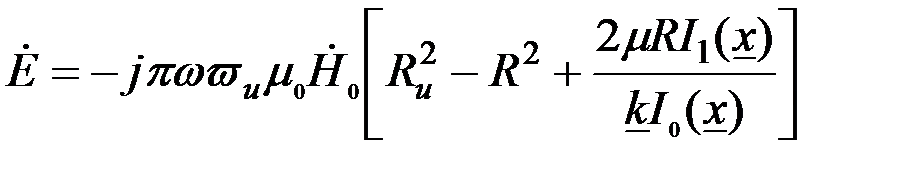 (3.78)
(3.78)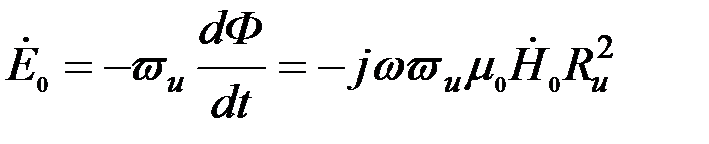 . (3.79)
. (3.79) , (3.80)
, (3.80)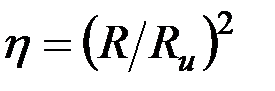 – коэффициент заполнения, равный отношению площади поперечного сечения контролируемого цилиндра к площади, охватываемой контуром измерительной обмотки, если ее радиус меньше радиуса возбуждающей катушки. При размещении измерительной обмотки поверх возбуждающей катушки, т.е. при
– коэффициент заполнения, равный отношению площади поперечного сечения контролируемого цилиндра к площади, охватываемой контуром измерительной обмотки, если ее радиус меньше радиуса возбуждающей катушки. При размещении измерительной обмотки поверх возбуждающей катушки, т.е. при 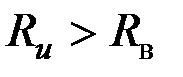 , коэффициент заполнения равен
, коэффициент заполнения равен 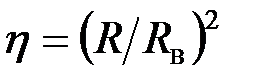 , поскольку поле вне возбуждающей катушки не влияет на вихревые токи в ОК. Таким образом,
, поскольку поле вне возбуждающей катушки не влияет на вихревые токи в ОК. Таким образом, при
при 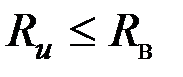 или
или 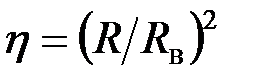 при
при 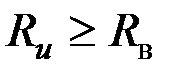 . (3.81)
. (3.81)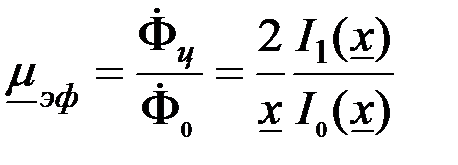 . (3.82)
. (3.82)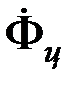 – магнитный поток, пронизывающий цилиндр при данном значении
– магнитный поток, пронизывающий цилиндр при данном значении  ;
; 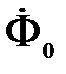 – магнитный поток через то же сечение при отсутствии цилиндра. Из определения и выражения (3.82) очевидно, что эффективная магнитная проницаемость не эквивалентна магнитной проницаемости
– магнитный поток через то же сечение при отсутствии цилиндра. Из определения и выражения (3.82) очевидно, что эффективная магнитная проницаемость не эквивалентна магнитной проницаемости  , характеризующей интенсивность намагничивания ферромагнетика, и эти понятия следует разделять.
, характеризующей интенсивность намагничивания ферромагнетика, и эти понятия следует разделять.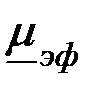 в (3.80), получаем
в (3.80), получаем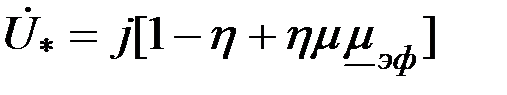 . (3.83)
. (3.83)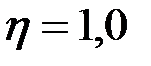 (т.е. при
(т.е. при 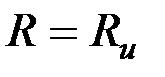 ) для ферромагнитного цилиндра следует
) для ферромагнитного цилиндра следует 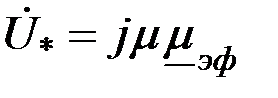 , а для неферромагнитных цилиндров (т.е.
, а для неферромагнитных цилиндров (т.е. 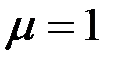 ) следует
) следует  . График
. График 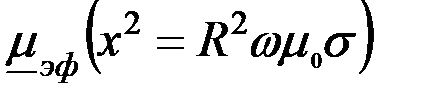 приведен на рис. 3.19.
приведен на рис. 3.19.
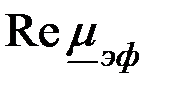
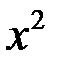 х2
х2
 от квадрата обобщенного параметра
от квадрата обобщенного параметра 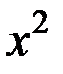
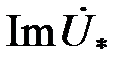
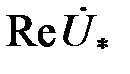
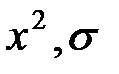

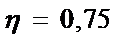
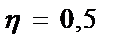
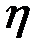

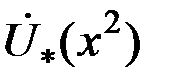 наружного проходного ВТП при контроле кругового неферромагнитного цилиндра
наружного проходного ВТП при контроле кругового неферромагнитного цилиндра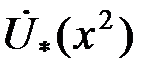 наружного проходного ВТП для проводящего немагнитного (
наружного проходного ВТП для проводящего немагнитного ( 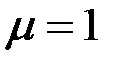 ) цилиндра при
) цилиндра при 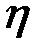 = 0,5; 0,75; 1,0 и
= 0,5; 0,75; 1,0 и 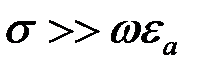 , т.е. когда плотность вихревых токов значительно больше плотности токов смещения. Основной годограф (при
, т.е. когда плотность вихревых токов значительно больше плотности токов смещения. Основной годограф (при 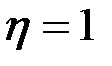 ) отличается от приведенного на рис. 3.19 лишь множителем
) отличается от приведенного на рис. 3.19 лишь множителем  , т.е.
, т.е.  . Этот годограф показывает зависимость напряжения
. Этот годограф показывает зависимость напряжения 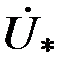 от удельной электрической проводимости
от удельной электрической проводимости  при
при  , так как
, так как 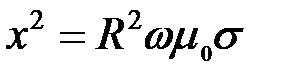 .
.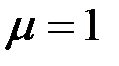 следует, что
следует, что , (3.84)
, (3.84) – это прямые линии (красные сплошные на рис. 3.20).
– это прямые линии (красные сплошные на рис. 3.20).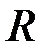 изменяются значения коэффициента заполнения
изменяются значения коэффициента заполнения 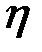 и обобщенного параметра
и обобщенного параметра  , а следовательно, и величина
, а следовательно, и величина 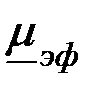 , поэтому годографы
, поэтому годографы 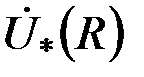 непрямолинейны (красные штриховые линии на рис. 3.20).
непрямолинейны (красные штриховые линии на рис. 3.20).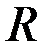 и
и  контролируемого цилиндра годографы
контролируемого цилиндра годографы  и
и 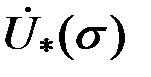 имеют различные направления, что позволяет раздельно контролировать указанные параметры цилиндра. Наилучшие условия раздельного контроля
имеют различные направления, что позволяет раздельно контролировать указанные параметры цилиндра. Наилучшие условия раздельного контроля 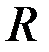 и
и  существуют тогда, когда углы между годографами
существуют тогда, когда углы между годографами 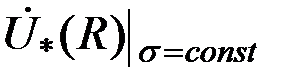 и
и 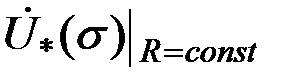 стремятся к
стремятся к  .
.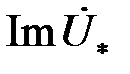

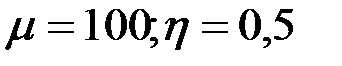

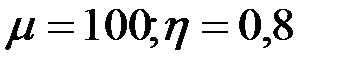

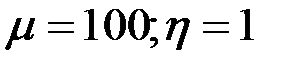
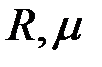

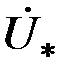 наружного проходного ВТП при изменении параметров ферромагнитного цилиндра для
наружного проходного ВТП при изменении параметров ферромагнитного цилиндра для 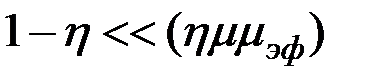
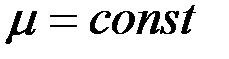 . Абсолютная магнитная проницаемость материала цилиндра
. Абсолютная магнитная проницаемость материала цилиндра 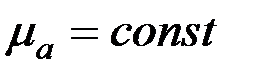 и при условии
и при условии 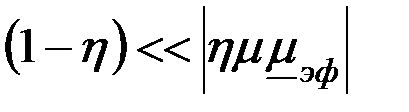 зависимости
зависимости  имеют вид, показанный на рис. 3.21. Из рисунка видно, что при
имеют вид, показанный на рис. 3.21. Из рисунка видно, что при 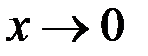 напряжение
напряжение  в
в  раз больше, чем при
раз больше, чем при  . Это объясняется тем, что магнитный поток в ферромагнитном протяженном цилиндре, расположенном в однородном магнитном поле, в
. Это объясняется тем, что магнитный поток в ферромагнитном протяженном цилиндре, расположенном в однородном магнитном поле, в 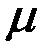 раз больше, чем в неферромагнитном. При
раз больше, чем в неферромагнитном. При  напряжение
напряжение 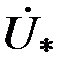 уменьшается в результате действия вихревых токов и при
уменьшается в результате действия вихревых токов и при 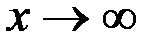 следует
следует 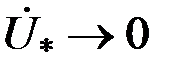 . Из рис. 3.21 видно, что направления изменения
. Из рис. 3.21 видно, что направления изменения 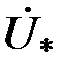 на комплексной плоскости при изменении
на комплексной плоскости при изменении 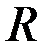 и
и  совпадают.
совпадают.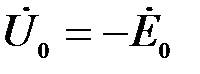 обычно компенсируют, поэтому за сигнал принимают относительное вносимое напряжение
обычно компенсируют, поэтому за сигнал принимают относительное вносимое напряжение 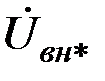 , возникающее при внесении контролируемого цилиндра в наружный проходной ВТП:
, возникающее при внесении контролируемого цилиндра в наружный проходной ВТП: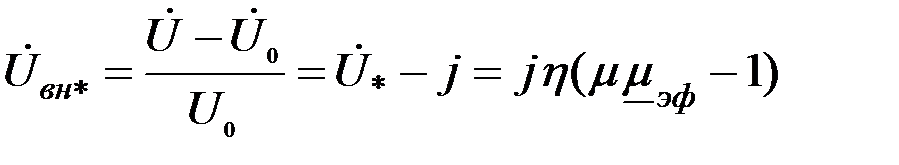 . (3.85)
. (3.85)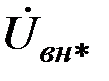 с увеличением
с увеличением  монотонно возрастает от нуля до единицы.
монотонно возрастает от нуля до единицы. :
: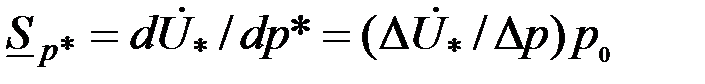 , (3.86)
, (3.86)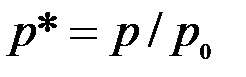 ,
, 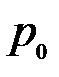 – номинальное значение параметра
– номинальное значение параметра 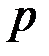 .
.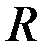 ,
,  и
и 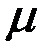 однородного кругового цилиндра при условии
однородного кругового цилиндра при условии 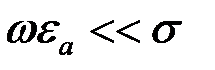 имеют вид
имеют вид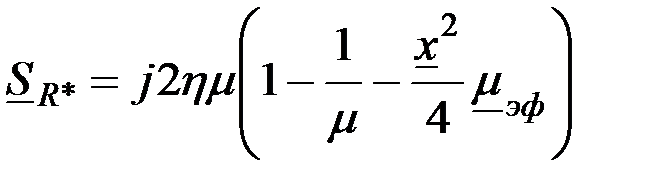 ; (3.87)
; (3.87)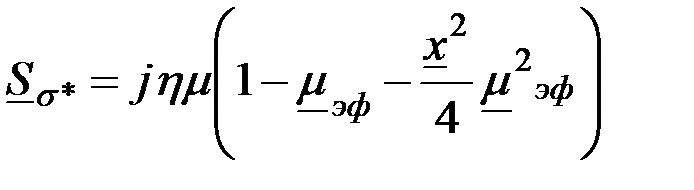 ; (3.88)
; (3.88)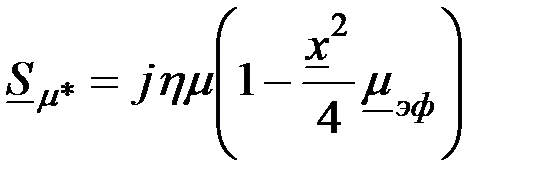 . (3.89)
. (3.89) к изменению радиуса
к изменению радиуса 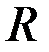 , удельной электрической проводимости
, удельной электрической проводимости  (при
(при  ) и магнитной проницаемости
) и магнитной проницаемости  (при
(при 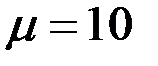 ). Направления векторов
). Направления векторов 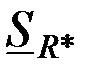 ,
, 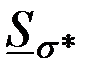 и
и 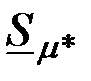 соответствуют направлениям касательных к соответствующим годографам рис. 3.20 для рассматриваемых значений
соответствуют направлениям касательных к соответствующим годографам рис. 3.20 для рассматриваемых значений 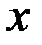 . На рис. 3.22 показаны векторы
. На рис. 3.22 показаны векторы 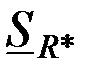 ,
, 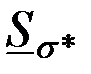 и
и 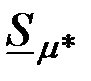 для
для 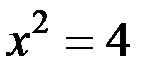 . Модули векторов рис. 3.22 пропорциональны приращениям
. Модули векторов рис. 3.22 пропорциональны приращениям  , обусловленным изменением контролируемых параметров
, обусловленным изменением контролируемых параметров  ,
,  или
или 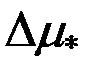 .
.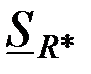 ,
, 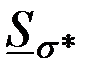 и
и 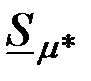 от
от 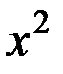 при тех же значениях коэффициента заполнения
при тех же значениях коэффициента заполнения  и проницаемости
и проницаемости 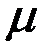 , что и годографы на рис. 3.22а-в.
, что и годографы на рис. 3.22а-в.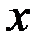 чувствительность
чувствительность 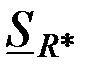 растет, стремясь к значению
растет, стремясь к значению  ;
; 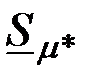 уменьшается до нуля при
уменьшается до нуля при 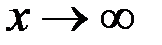 ; а чувствительность
; а чувствительность  вначале возрастает от нуля до
вначале возрастает от нуля до 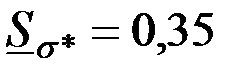 при
при 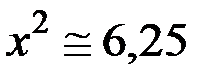 , а затем уменьшается, стремясь к нулю при
, а затем уменьшается, стремясь к нулю при 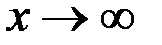 .
. ; для контроля магнитной проницаемости – малым значениям
; для контроля магнитной проницаемости – малым значениям 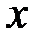 ; а для контроля удельной электрической проводимости – значению
; а для контроля удельной электрической проводимости – значению 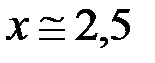 .
.