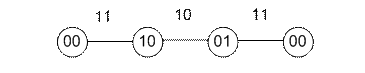
Свободное расстояние сверточного кода.

Мерой помехоустойчивости сверточного кода является, как правило, вероятность ошибочного приема либо отдельного символа, либо блока сим­волов в целом. Однако помехоустойчивость декодирования зависит и от дис­танционных свойств кодовых последовательностей на выходе кодера. При этом чаще всего расстояние между последовательностями оценивают с помощью мет­рики Хэмминга.

Так, свободное расстояние d_f (d_free) - это минимальное расстояние между двумя произвольными полубесконечными последовательностями на выходе кодера, отличающимися в первой ветви. Для коротких кодов свобод­ное расстояние легко определить по диаграмме состояний кода. Свободное расстояние кода равно минимальному весу пути по диаграмме из состояния 00 в тоже состояние (исключая петлю у состояния 00). Диаграмма свободного расстояния для рисунка 3.3 изображена на рисунке 3.5 и для него d_f =5. Для нерекурсивного кодера это вес отклика кодирующего устройства на единичный символ. Свободное расстояние d_f используется для оценки помехоустойчивости декодирования сверточных кодов. Этот пара­метр аналогичен минимальному кодовому расстоянию d_min , которое харак­теризует помехозащитные свойства блоковых кодов. Свободное расстояние показывает, сколько ошибок может произойти в канале связи, чтобы одна кодовая последовательность перешла в другую, и эти ошибки не были бы обнаружены декодером.

Рисунок 3.5. – Диаграмма состояний сверточного кодера для нахождения свободного расстояния.

Декодирование Витерби.

Известен ряд алгоритмов декодирования сверточных кодов. В практических системах и, в частности в мобильной связи, как правило, используется алгоритм Витерби, отличающийся про­стотой реализации при умеренных длинах кодового ограничения.

Алгоритм Витерби реализует оптимальное (максимально правдоподобное) декодирование как рекуррентный поиск на ко­довой решетке пути, ближайшего к принимаемой последователь­ности. На каждой итерации алгоритма Витерби сопоставляются два пути, ведущих в данное состояние (узел решетки). Ближай­ший из них к принятой последовательности сохраняется для дальнейшего анализа как выживший, тогда как другой отбрасы­вается. Таким образом, если игнорировать случаи, когда оба конкурирующих пути равноудалены от принятой последователь­ности, число выжив­ших путей, сохраняемых в памяти, равно числу узлов 2^т.

Пусть передается нулевое кодовое слово, а в канале про­изошла трехкратная ошибка, так что принятая последователь­ность имеет вид 10 10 00 00 10 00 ... 00 ... Результаты поиска ближайшего пути после приема 14 элементарных блоков показа­ны на рис. 3.6.

На правой части рисунка видны четыре пути, ведущие в каж­дый узел решетки. Рядом проставлены метрики (хэмминговы рас­стояния этих путей от принятой последовательности на отрезке из 14 блоков). Метрика верхнего пути значительно меньше метрик нижних. Поэтому можно предположить, что верхний путь наиболее вероятен. Однако декодер Витерби, не зная следующих фрагмен­тов принимаемой последовательности, вынужден запомнить все четыре пути на время приема L элементарных блоков. Число L на­зывается шириной окна декодирования. Для уменьшения ошибки декодирования величину L следует выбирать достаточно большой, многократно превышающей длину кодового ограничения, что есте­ственно усложняет декодер. В данном случае L = 15.

Отметим, что тактика выбора и последующего анализа только одного пути с наименьшим расстоянием составляет сущ­ность более экономного последовательного декодирования.

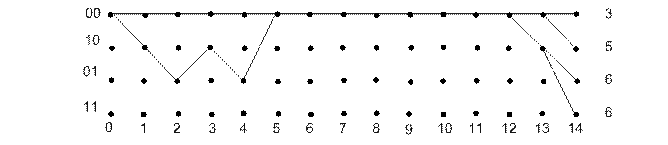
Рисунок 3.6. – Пример работы алгоритма Витерби.

На средней части рисунке 3.6 видно, что все пути имеют общий отрезок (сливаются от 5-го до 12-го шага) и, следовательно, при­ем новых блоков не может повлиять на конфигурацию этого уча­стка наиболее правдоподобного пути. Поэтому декодер уже мо­жет принимать решение о значении информационных символов, соответствующих этим элементарным блокам.

Левая часть рисунка демонстрирует возможную ситуацию неисправляемой ошибки. Существует два пути с одинаковыми метриками. Декодер может разрешить эту неопределенность двумя способами: отметить этот участок как недостоверный или принять одно из двух конкурирующих решений (информационная последовательность равна 00000... или 10100...). Очевидно, что расширение окна декодирования не позволяет исправить такую ошибку. Ее исправление возможно при использовании кода с большей корректирующей способностью.

Поступление из канала нового элементарного блока вызы­вает сдвиг картинки в окне декодирования влево. В результате левое ребро пути исчезает, а справа появляется новый столбец решетки, к узлам которого должны быть продолжены сохранен­ные пути от узлов предыдущего столбца. Для этого выполняются следующие операции.

1. Для каждого узла нового столбца вычисляются расстоя­ния между принятым блоком и маркировкой ребер, ведущих в данный узел.

2. Полученные метрики ребер суммируются с расстоянием путей, которые они продолжают.

3. Из двух возможных путей оставляется путь с меньшей метрикой, а другой отбрасывается, так как следующие поступаю­щие блоки не могут изменить соотношения расстояний этих пу­тей. В случае равенства расстояний или случайно выбирается один путь, или сохраняются оба.

В результате этих операций к каждому узлу нового столбца вновь ведет один путь. Например, пусть новый блок из канала равен 00. Рассмотрим продолжение пути к нижнему узлу решетки, в который можно попасть из состояния кодера 10 по ребру 01 или из состояния 11 по ребру 10 (см. рис. 3.4). В обоих случаях рас­стояние этих ребер от принятого блока 00 равно 1. Однако сум­марное расстояние пути, продолженного из состояния 10, равно 6, а пути из состояния 11 равно 7. Поэтому второй путь будет от­брошен вместе с ребром 01, которое входило в нижний узел на предыдущем шаге декодирования (см. рис. 3.6).

Оценка информационного символа производится по край­нему левому ребру пути в окне декодирования. Согласно правилу построения кодовой решетки принимается, что информационный символ равен 0, если это ребро верхнее, и 1, если ребро нижнее. Рассмотренный пример поясняет работу декодера в пред­положении, что выходной сигнал демодулятора квантуется на 2 уровня (так называемое жесткое декодирование). Большее число уровней квантования приводит к мягкому декодированию. Установлено, что 8 уровней квантования гарантируют практиче­ски потенциальную достоверность декодирования.

Не нашли, что искали? Воспользуйтесь поиском по сайту: