Подготовка к выполнению работы

3.1 По рекомендованной литературе и настоящим методическим указа­ниямизучить:

- принципы кодирования и декодирования циклических кодов;

- правило построения схемы устройства формирования проверочных элементов;

- процесс формирования проверочных разрядов;

- схемы декодирования циклических кодов.

3.2 Осуществить кодирование кодовой информации 1101 с помощью образующего полинома (см. таблицу 3.1) по варианту заданному преподавателем.

Таблица 3.1

4. Выполнения работы

Вы работаете с обучающее - контролирующей программой и должны внимательно отнестись к ее вопросам и указаниям.

Согласно варианту предлагается образующий полином Р(х) и информационная последовательность, их надо записать в отчет. На основании заданного полинома Р(х) рассматриваются два варианта схем коде­ров. Формирование проверочных разрядов прослеживается заполнением таблиц. Схемы и таблицы занести в отчет. Отметить особенности рассмотренных схем кодеров.

Изучению предлагается схема декодера с обнаружением ошибок и рассматривается процесс декодирования двух комбинаций циклического кода. Схемы декодера и таблицы занести в отчет.

Программа имеет счетчик ошибок и таймер времени. По окончании работы информация о количестве правильных ответов и время выводится на экран и преподаватель учитывает ее при оценке работы студента.

Содержание отчета

Отчет по лабораторной работе должен содержать:

- цель работы

- пример составления кодовой комбинации для заданного варианта

- схемы кодеров и таблицы формирования проверочных разрядов

- схему декодера и таблицу формирования синдрома ошибки.

6. Контрольные вопросы

1. Что такое кодовое расстояние?

2. Сколько ошибок код может обнаружить или исправить, от чего это зависит?

3. Поясните процесс кодирования в циклическом коде.

4. Поясните принцип декодирования собнаружением ошибок.

5. В чем состоит принцип декодирования с исправлением ошибки?

6. Что такое "синдром ошибки"?

7. Поясните структуру схем кодеров и их варианты.

8. Поясните структуру схемы декодера.

Литература

1. Шувалов В.П., Захарченко А.В., Шварцман В.О. и др. Передача дискретных сообщений. -М.: Радио и связь, 1990, стр. 282-286.

2. Системы мобильной связи : Учебное пособие для вузов/ В. П. Ипатов. В. К. Орлов, И. М. Самойлов, В. Н. Смирнов; под ред. В. П. Ипатова. – М.: Горячая линия – Телеком, 2003.

3. Компьютерные сети. Принципы, технологии, протоколы / В.Г. Олифер, Н.А. Олифер. - СПб.:Питер, 2002.-672 с.

ЛАБОРАТОРНАЯ РАБОТА № 3

«Исследование сверточного кода»

Цель работы.

1.1 Изучить работу кодера и декодера сверточных кодов по алгоритму Витерби.

1.2 Проанализировать исправляющую способность декодера.

Подготовка к выполнению работы.

2.1. Изучить принцип действия сверточных кодов и декодирования методом Витерби по литературе и методическим указаниям к работе.

2.2. Составить диаграмму состояний для сверточного кода с R=1/2.

Основные теоретические сведения.

Сверточные коды.

Сверточные коды представляют собой обширный класс корректирую­щих кодов. Они были предложены в 1955 году Элайсом и в настоящее время нашли широкое применение в системах радиосвязи, включая спутни­ковые каналы и каналы мобильной связи. Сверточные коды используются при передачи речевых сообщений в системах с малой временной задержкой (системы реального времени). Сверточные коды можно рассматривать как частный случай блоко­вых кодов, но наличие сверточной структуры наделяет его дополнительными свойствами, улучшающими его характеристики.

Как любой корректирующий код, сверточные коды защищают инфор­мацию, добавляя избыточные символы. Кодирующее устройство сверточного кода со скоростью R = k/n (рис. 3.1) обрабатывает входную последователь­ность, состоящую их k информационных символов, и вычисляет п кодовых (канальных) символов (n > к). Если один (например первый) из n символов текущего блока повторяет текущий информационный бит, код называется систематическим.

Рассматриваемый здесь код называется сверточным, так как последо­вательность кодовых символов {b_j} может быть получена как цифровая свертка информационных символов {а_j}с импульсным откликом кодера {g_ij}. Кроме того, значение выходного символа b_j с номером t получается как линейная комбинация т преды­дущих информационных символов {a_j} , i є [t- т,..., t], где т - ха­рактеризует память кодера. Вообще, существует несколько характеристик для определения длины памяти при кодировании. Длина кодирующего регистра т равна количеству ячеек памяти, содержащихся в кодирую­щем устройстве. Этот параметр обычно используется для определе­ния памяти кодера при кодировании со скоростью R= 1/2 (рисунке 3.2.).

Рисунок 3.1. – Структура кодирующего устройства со скоростью R=k/n.

На рисунке 3.2 приведен пример несистематического нерекурентного сверточного кодера со скоростью R = k/n и длиной кодирующего регистра m=3

( где m – характеризует память кодера, предшествующих битов).Существует еще один параметр кода - длина кодового огра­ничения v, связанная для сверточных кодов при R = 1/2 с длиной кодирующего регистра следующим соотношением:

v = т - 1.

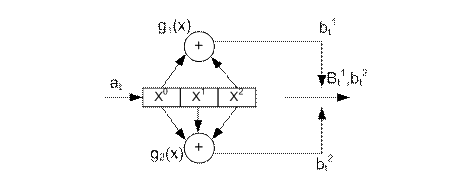
Рисунок 3.2. – Сверточный кодер с R=1/2.

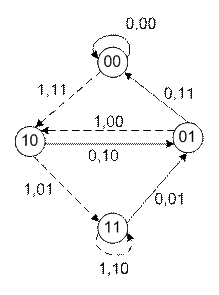
Сверточный кодер с кодовым ограничением v представляет собой регистр памяти для хранения т информационных символов и преобразова­тель информационной последовательности в кодовую последовательность. Процесс кодирования производится непрерывно. Информационные двоич­ные символы {a_i}поступают на вход регистра сдвига с т ячейками, в кото­ром символы кодовой последовательности формируются суммированием по модулю 2 символов с выходов некоторых ячеек. Подключение сумматоров к ячейкам регистра задается генераторными полиномами g₁(x) и g₂(x): g₁(x)=1+x² , g₂(x)=1+x+x² или g₁(x)=101 и g₂(x)=111. За время одного информа­ционного символа на выходе образуются два кодовых символа (см. рис. 3.2).

Существуют несколько способов представления сверточных кодов: с использованием кодового дерева (решетчатых диаграмм), с помощью матриц и представление с помощью оператора задержки.

Сверточный кодер можно рассматривать как постоянный во времени конечный автомат, структура которого является периодической и может быть описана с помощью различных диаграмм. Например, сверточный кодер мо­жет быть описан диаграммой состояний. Диаграмма представляет собой на­правленный граф и описывает все возможные переходы кодера из одного состояния в другое, а также содержит выходные символы кодера, которые сопровождают эти переходы. Состояние кодера - содержимое т -1 левых (или правых) ячеек регистра памяти. Пример диаграммы состояний показан на рисунке 3.3.

В кружках указаны четыре возможных состояния кодера 00, 10, 01, 11, линиями со стрелками - возможные переходы. Сплошная линия отмечает переходы, совершаемые при поступлении на вход кодирующего устройства информационного символа 0, пунктирная - при поступлении символа 1. Сим­волы около линий обозначают символы на входе и выходе кодера (a_i, b_i¹b_i²), соответствующие данному переходу.

Решетчатая диаграмма является разверткой диаграммы состояний во времени. На рисунке 3.4. показан пример решетчатой диаграммы.

Рисунок 3.3. – Диаграмма состояний сверточного кодера.

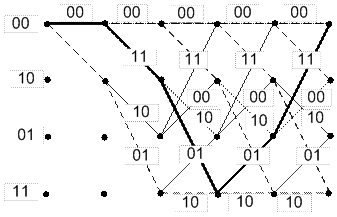
Рисунок 3.4. – Решетчатая диаграмма сверточного кодера с кодовым ограничением 2.

На решетке состояния кодера показаны узлами, а переходы - соединяющими их линиями. После каждого перехода из одного состояния в другое происходит сме­щение на один шаг вправо. Решетчатая диаграмма дает наглядное представление всех разрешенных путей, по которым мо­жет продвигаться кодер при кодировании. Каждой информационной последователь­ности на входе кодера соответствует един­ственный путь по решетке.

Решетчатая диаграмма удобна для наглядного пояснения принципов декоди­рования сверточных кодов. Следует отме­тить, что в двоичном симметричном канале оптимальной оценкой переданной кодовой комбинации слова является комбинация, ближайшая (в смысле расстояния по Хеммингу) к принятой. Это и есть путь по кодовой решетке, отстоящий от последовательности на минимальное расстояние по Хеммингу. Поиск такого мак­симально правдоподобного пути и составляет сущность алгоритма декодиро­вания Витерби, который будет рассмотрен ниже.

Не нашли, что искали? Воспользуйтесь поиском по сайту: