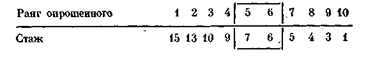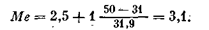Среднее значение признака.

Среднее есть абстрактная типическая характеристика всей совокупности. Оно уничтожает, погашает, сглаживает случайные и неслучайные колебания, влияние индиви­дуальных особенностей и позволяет представить в одной величине, некоторую общую характеристику реальной совокупности единиц. Основное условие научного использования средних заключается в том, чтобы каждое среднее характеризовало такую совокупность единиц, которая в существенном отношении, и в первую очередь в отношении осредняемых значений признака, была бы качественно однородной. Среди всего многообразия средних практически наибо­лее часто используемой считается среднее арифметическое.

Среднее арифметическое. Среднее арифметическое есть частное от деления суммы всех значений признака на их число. Обознача­ется оно х. Формула для вычисления имеет вид

По следующим данным вычислим среднее число газет, читаемых ежедневно индивидами в выборке, из 10 человек:

Формула (1) для сгруппированных данных преобразуется в следующую:

где n_t — частота для i-го значения признака.

Если находят среднюю для интервального ряда .распределения, то в качестве значения признака для каждого интервала условно принимают его середину.

Процедуру вычисления среднего по сгруппированным данным удобно выполнять по следующей схеме (табл. 3).

Существует ряд упрощенных приемов вычисления средних. На с. 163 как промежуточный этап рассмотрено вычисление среднего методом отсчета от условного нуля.

Пример. Вышеприведенные данные о количестве прочитанных газет (см. с. 159) сгруппируем следующим образом:

Медиана. Медианой называется значение признака у той еди­ницы совокупности, которая расположена в середине ряда частот­ного распределения.

Если в ряду четное число членов (2k), то медиана равна средне­му арифметическому из двух серединных значений признака. При нечетном числе членов (2k+ 1) медианным будет значение призна­ка у (k + 1) объекта.

Предположим, что в выборке из 10 человек респонденты проранжированы по стажу работы на данном предприятии:

Серединные ранги 5 и 6, поэтому медиана равна

В интервальном ряду с различными значениями частот вычисление медианы распадается на два этапа: сначала находят медиан­ный интервал, которому соответствует первая из накопленных ча­стот, превышающая половину всего объема совокупности, а затем находят значение медианы по формуле

где Х0 — начало (нижняя граница) медианного интервала; d — ве­личина медианного интервала; n = Sn_t — сумма частот (относитель­ных частот) интервалов; n_н — частота (относительная), накоплен­ная до медианного интервала; n_мe — частота (относительная) меди­анного интервала.

Проведем вычисление по данным табл. 2, где в нижней строке приведены накопленные относительные частоты. Первая из них, превышающая половину совокупности (100/2 = 50%), равна 57,9%. Следовательно, медиана принадлежит интервалу 3—4 года. По­этому

Таким образом, для данной выборки медиана, равная 3,7 года, показывает, что 50% семей имеют соотношение возрастов, меньшее этой величины, а другие 50%—большее. Медиана может быть легко определена графически по кумуляте распределения (см. рис. 3).

Медиана может быть применена для дискретных переменных, хотя дробные значения часто не имеют непосредственной содержа­тельной интерпретации.

По данным распределения рабочих по тарифным разрядам см. с. 156) вычислим медиану этого распределения, используя приведенную выше формулу¹⁸. Получим

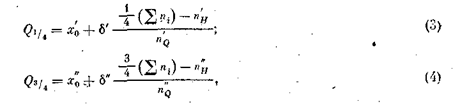
Узнали, что 50% рабочих имеют разряд, меньший 3,1, и 50%—больший.

Медиана, как уже отмечалось, делит упорядоченный вариацион­ный ряд на две равные по численности группы.

Наряду с медианой можно рассматривать величины, называемые квантилями, которые делят ряд распределения на 4 равные части, на 10 и т. д.

Квантили, которые делят ряд на 4 равные по объему совокупно­сти, называются квартилями. Различают нижний Q1/4 и верхний квартили (рис. 6). Величина Q_1/2 является медианой. Вычисле­ние квартилей совершенно аналогично вычислению медианы:

где х₀ — минимальная граница интервала, содержащего нижний (верхний) квартиль; n_н — частота (относительная частота), накоп­ленная до квартального интервала; n_Q — частота (относительная частота) квартального интервала; d — величина квартального ин­тервала.

Процентили делят множество наблюдений на 100 частей с рав­ным числом наблюдений в каждой. Децили делят множество наблю­дений на десять равных частей. Квантили легко вычисляются по распределению накопленных частот (по кумуляте).

Мода. Модой в статистике называется наиболее часто встречаю­щееся значение признака, т. е. значение, с которым наиболее веро­ятно можно встретиться в серии зарегистрированных наблюдений. В дискретном ряду мода (Мо) — это значение с наибольшей частотой.

В интервальном ряду (с равными интервалами) модальным яв­ляется класс с наибольшим числом наблюдений. Значение моды находится в его пределах и вычисляется по формуле

где х₀ — нижняя граница модального интервала; d — величина ин­тервала; n- — частота интервала, предшествующего модальному; n_Мо — частота модального класса; n⁺ — частота интервала, следую­щего за модальным.

В совокупностях, в которых может быть произведена лишь опе­рация классификации объектов по какому-нибудь качественному признаку, вычисление моды является единственный способом ука­зать некий центр тяжести совокупности.

К недостаткам моды следует отнести следующие: невозможность совершать над ней алгебраические действия; зависимость ее величи­ны от интервала группировки; возможность существования в ряду распределения нескольких модальных значений признака (см., например, рис. 4, в).

Сравнение средних. Целесообразность использования того или иного типа средней величины зависит по крайней мере от следующих условий: цели усреднения, вида распределения, уровня измерения признака, вычислительных соображений. Цель усреднения свя­зана с содержательной трактовкой рассматриваемой задачи. Однако форма распределения может существенно усложнить исследование средних. Если для симметричного распределения (см. рис. 4, а) мода, медиана и среднее арифметическое тождественны, то дляасимметричного распределения это не так. На выбор средней мо­жет повлиять и вид распределения. Например, для ряда с откры­тыми конечными интервалами нельзя вычислять среднее арифмети­ческое, но если распределение близко к симметричному, можно под­считать тождественную ему в этом случае медиану.

Не нашли, что искали? Воспользуйтесь поиском по сайту: