
|
|
Расчеты на прочность бруса круглого поперечного сеченияТема 11. Общий случай нагружения бруса круглого и прямоугольного поперечного сечения. Расчеты на прочность Алгоритм расчета на прочность при сложном нагружении В общем случае нагружения в поперечном сечении бруса возникает шесть внутренних силовых факторов. В предыдущих лекциях были рассмотрены методы расчета на прочность и жесткость при действии отдельных факторов: нормальной силы; поперечных сил; крутящего и изгибающего моментов.
Рис.11.1. Интегральные внутренние силовые факторы в сечении при сложном нагружении
Известно, что при действии нормальной силы N и двух изгибающих моментов Мх и Мy в поперечных сечениях возникают нормальные напряжения, направленные перпендикулярно к сечению. От крутящего момента Мкр и от поперечных сил Qx и Qy возникают касательные напряжения. При этом касательные напряжения, определяемые по формуле Журавского, направлены параллельно поперечным силам, т.е. вдоль главных центральных осей сечения. Касательные напряжения от крутящего момента в брусе круглого поперечного сечения направлены перпендикулярно радиусу, проведенному в рассматриваемую точку, а для сечения произвольной формы величина и направление касательных напряжений вычисляются методами теории упругости. Очевидно, что зная направление и величину касательных напряжений в данной точке, их можно разложить на составляющие по главным центральным осям. С учетом приведенных замечаний напряженное состояние бруса в произвольной точке поперечного сечения можно представить в виде, показанном на рис.11.2.
Рис.11.2. Напряженное состояние в точке при сложном нагружении
Нормальные напряжения
Касательные напряжения равны алгебраической сумме составляющих, параллельных главным центральным осям инерции сечения от поперечных сил - Если определены действующие во всех точках поперечных сечений бруса нормальные и касательные напряжения, вычисленные по известным формулам для простых видов нагружения (растяжение, сдвиг, кручение, изгиб), то можно найти главные напряжения. Затем, используя одну (или несколько) гипотез прочности проверить прочность бруса в рассматриваемых точках. При проверке прочности элементов конструкции сопоставляют максимальные расчетные напряжения в данной точке (расчетные напряжения в опасных точках) с допускаемыми напряжениями. Последовательность расчетов на прочность, как правило, следующая: - строят эпюры внутренних силовых факторов, по которым в первом приближении определяют опасные сечения, т.е. такие сечения, в которых интегральные внутренние усилия достигают максимальных значений; - анализируют распределение напряжений по опасным сечениям и выявляют наиболее нагруженные (опасные) точки сечений. Особое внимание уделяется точкам, в которых и нормальные и касательные напряжения максимальны (опасное сочетание внутренних усилий); - вычисляют расчетные напряжения в опасных точках и сопоставляют с допускаемыми напряжениями. Делают выводы о прочности конструкции.
Расчеты на прочность бруса круглого поперечного сечения Рассмотрим более подробно алгоритм проверки прочности бруса круглого поперечного сечения, который часто встречается в элементах конструкции машин и механизмов (валы редукторов, винтовых механизмов; валы кривошипно-шатунных механизмов и др.). Предположим, что в поперечных сечениях бруса возникают все шесть внутренних силовых факторов. Проанализируем распределение напряжений по сечению. От поперечной силы N нормальные напряжения σN будут распределены равномерно по сечению, как показано на рис. 11.3.
Рис.11.3. Распределение напряжений при сложном нагружении вала
Заменим изгибающие моменты Мx и Мy суммарным изгибающим моментом МΣ, модуль которого будет равен где Максимальные по модулю нормальные напряжения от изгиба возникают в точках А и В, наиболее удаленных от оси Oy1 (x1=D/2). В этих же точках максимального значения достигают касательные напряжения от крутящего момента Мкр=Мz. Максимальные касательные напряжения от поперечных сил Qx и Qy возникают в точках, расположенных соответственно на осях Oy и Ox и их величина в большинстве случаев существенно меньше касательных напряжений от кручения, что позволяет ими пренебречь. Сравнивая напряжения в точках А и В, находим опасную точку, т.е. точку, в которой максимальные нормальные напряжения от изгиба суммируются с максимальными нормальными напряжениями от продольной силы. В рассматриваемом примере – это точка А. В этой точке будут действовать: - нормальные напряжения от суммарного изгибающего момента - нормальные напряжения от продольной силы - касательные напряжения от кручения Напряженное состояние в точке А – плоское. Условия прочности по гипотезе максимальных касательных напряжений можно записать в виде
где В частном случае при N=0 условия прочности принимают вид
Учитывая, что Wp=2Woc, находим
Числитель в формуле (11.2) называют приведенным моментом. По гипотезе максимальных касательных напряжений он равен
При использовании гипотезы энергии формообразования эквивалентные напряжения при расчете прочности равны
Тогда выражение для приведенного момента при сложном нагружении примет вид:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 равны алгебраической сумме напряжений от продольной силы N -
равны алгебраической сумме напряжений от продольной силы N -  и двух изгибающих моментов
и двух изгибающих моментов  и
и 
 .
.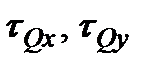 и от крутящего момента
и от крутящего момента  и
и  . Следовательно,
. Следовательно,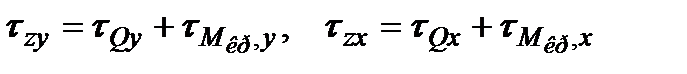 .
. . При действии суммарного изгибающего момента МΣ изгиб будет происходить относительно оси Oy1 (рис. 11.2), совпадающей с направлением вектора МΣ, а напряжения, учитывая, что оси Ox1 и Oy1 также являются главными центральными осями вала, можно определить по известным формулам для поперечного изгиба
. При действии суммарного изгибающего момента МΣ изгиб будет происходить относительно оси Oy1 (рис. 11.2), совпадающей с направлением вектора МΣ, а напряжения, учитывая, что оси Ox1 и Oy1 также являются главными центральными осями вала, можно определить по известным формулам для поперечного изгиба .
. (D – диаметр вала).
(D – диаметр вала).


 . (11.1)
. (11.1)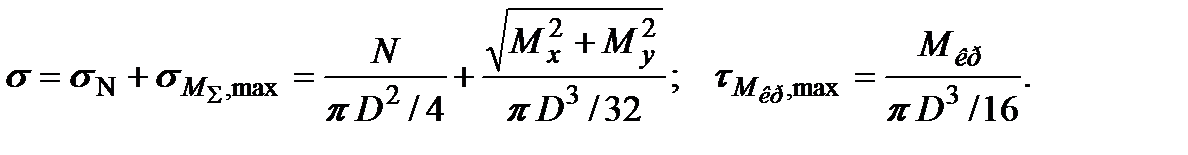

 (11.2)
(11.2) (11.3)
(11.3)
 (11.4)
(11.4)