
|
|
Интегрирование тригонометрических выраженийИнтегрирование рациональных функций Функция R(x) называется рациональной, если для вычисления её значений над аргументом Х выполняется только конечное число арифметических действий. Любую рациональную функцию можно представить в виде Теорема Безу: При делении многочлена на Qn(x) (n>0) на разность (х-с), где С произвольное число, получается остаток равный значению многочлена при х-с. Qn(x)=(x-c)Qn-1(x)+Qn(c), где Qn-1(x) – многочлен степени n-1 Следствие: если с - корень многочлена Qn(x), то Qn(x)=(х-с) Qn-1(x) Теорема 2 (основная теорема алгебры) Всякий многочлен Qn(x) степени n>0 имеет по крайней мере, один вещественный или комплексный корень. Всякий многочлен Qn(x) может быть представлен в виде Qn(x)=a0(x-c1) (x-c2)….(x-cn), где с1,с2,…,сn корни многочлена Qn(x), а k1k2km кратность соответствующего корня. Тогда a0(x-c1)k1 (x-c2)k2….(x-cn)km. Теорема 3 Если многочлен Qn(x) с вещественными коэфициентами имеет комплексный корень a+ib, кратности k, то сопряжённое число a-ib есть корень той же кратности. a+ib и a-ib – пара сопряжённых комплексных корней Qn(x). x2+px+q, где p=-2a, q=a2+b2 Вывод:Многочлен Qn(x) может быть представлен в виде произведения линейных и квадратичных можетелей (неразложимых на линейные вещественные множетели). Qn(x)= a0(x-c1)k1 (x-c2)k2….(x-cr)kr (x2+p1x+q1)L1….(x2+psx+qs)Ls, где множетели (x-c1)k1 (x-c2)k2….(x-cr)kr соответсвует вещественным корням c1,c2,cr Qn(x) кратности k1k2kr , а множетели (x2+p1x+q1)L1….(x2+psx+qs)Ls – S парам комплексно сопряжённых корней кратности L1,L2,Ls Интерестно, что (k1k2kr+ 2L1,2L2,2Ls=n). Простейшими дробыми 1 и 2 типа называются рациональные дроби вида A/(x-c)k; и Mx+N/(x2+p1x+q1)L, где k, L натуральные числа, а A,M,N,c,p,q –вещественные числа при условии, что p2-4q<0 Теорема 4 Всякая правельная рациональная дробь может быть предствавлена в виде суммы простейших дробей, так что каждому множетелю вида (x-c)k в разложении знаменателя отвечает сумма k простейших дробей первого типа. A1/x-c+A2/(x-c)2+……+Ak/(x-c)k, а каждому множителю вида (x2+psx+qs)L сумма из L простейших дробей 2-го типа (M1x+N1/ x2+px+q) + M2x+N2/( x2+px+q)2 + MLx+NL/( x2+px+q)L. Такое разложение единственно.
Интегрирование простейших рациональных функций 1. 2. 3. 4. 5.
Метод неопределённых коэффициентов Теорема №1 (о многочлене, тождественно равном нулю). Если при произвольных значениях аргумента x значение многочлена f(x) = а0+ а1х + а2х2 +...+ а nxn, заданного в стандартном виде, равно нулю, то все его коэффициенты а0, а1, а2, ..., аn равны нулю. Теорема №2 (следствие теоремы № 1). Пусть и f(x) = а0+а1х +...+ а nxn, и g (x)= b 0+ b 1х + b 2х2 +...+ bnxn. Для того чтобы f(x)= g(x)необходимо и достаточно, что бы а0= b0, а1 = b1, а2 = b 2 , ..., а n= bn Рассмотрим два многочлена
предположим, что При делении многочлена
Интегрирование тригонометрических выражений 1.Интегралы вида Интегралы указанного вида сводятся к интегралам от рациональной функции новой переменной t с помощью подстановки Замечание. Универсальная тригонометрическая подстановка часто приводит к громоздким вычислениям. Поэтому чаще применяются другие подстановки. 2.Подынтегральная функция или условию 3.Подынтегральная функция 4.Вычисление интегралов вида В этом случае полезно пользоваться следующими правилами: А) если m - нечетное положительное число, то вносим Б) если оба показателя m и n - четные положительные числа, то подынтегральную функцию преобразуют с помощью формул понижения степени: В) если число m+n является четным отрицательным числом, то можно сделать замену переменной Г) если степени m и n отрицательны, то часто бывает полезным уменьшить степени с помощью основного тригонометрического тождества. Примечание. В общем случае интегралы вида 5.При вычислении интегралов вида 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Пусть степень многочлена
. Пусть степень многочлена 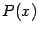 равна m , а степень Q(x) равна n , то есть
равна m , а степень Q(x) равна n , то есть  где
где  и
и  . Если m<n, то дробь R(x) называется правильной, а если
. Если m<n, то дробь R(x) называется правильной, а если  , то неправильной. Если дробь неправильная, то её числитель P(x) можно поделить на знаменатель R(x) , получив при этом частное S(x) и остаток T(x) , степень которого m’<n. Это означает, что
, то неправильной. Если дробь неправильная, то её числитель P(x) можно поделить на знаменатель R(x) , получив при этом частное S(x) и остаток T(x) , степень которого m’<n. Это означает, что  .
.
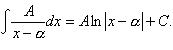

 заменой
заменой  сводится к линейной комбинации интегралов
сводится к линейной комбинации интегралов  и
и 
 заменой
заменой  и
и 
 степени m и n, соответственно
степени m и n, соответственно


 на многочлен
на многочлен  , где
, где  и
и  такие, чтобы выполнялось равенство
такие, чтобы выполнялось равенство 
 , где
, где  рациональная функция от u и v.
рациональная функция от u и v.
 , которую называют универсальной тригонометрической подстановкой. При этом используются формулы тригонометрии
, которую называют универсальной тригонометрической подстановкой. При этом используются формулы тригонометрии 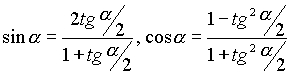
 удовлетворяет условию
удовлетворяет условию 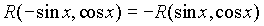
 . Тогда можно использовать подстановку
. Тогда можно использовать подстановку 
 или
или 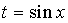
 соответственно.
соответственно. . Это условие выполняется в частности для функций, содержащих только четные степени
. Это условие выполняется в частности для функций, содержащих только четные степени  и
и 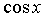 . В этом случае часто применяют замену переменной
. В этом случае часто применяют замену переменной  , где
, где  где
где  или
или  ,то
,то 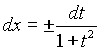 . Функции
. Функции  и
и  .
. , где m и n ? целые числа.
, где m и n ? целые числа. ,
,  и
и  .
. или
или  где m - натуральное число,
где m - натуральное число,  используют тригонометрические формулы
используют тригонометрические формулы  или, соответственно,
или, соответственно,  .
.