Исходное уравнение запишем в матричной форме
Исходное уравнение запишем в матричной форме
 , где , где  , ,  . .
Матричное уравнение вида  имеет решение, если матрицы имеет решение, если матрицы  и и  – квадратные матрицы одинакового порядка и матрица – квадратные матрицы одинакового порядка и матрица  – невырожденная, т.е. – невырожденная, т.е.  . В этом случае для матрицы . В этом случае для матрицы  существует обратная матрица существует обратная матрица  . Умножая слева обе части уравнения . Умножая слева обе части уравнения  на на  , получим , получим
 , где , где  единичная матрица, единичная матрица,
 искомая матрица. искомая матрица.
Для данной матрицы  : :  . Следовательно, существует . Следовательно, существует  . Найдем ее по формуле . Найдем ее по формуле 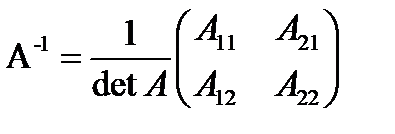 , где , где  алгебраическое дополнение элемента алгебраическое дополнение элемента  матрицы матрицы  . Для данной матрицы . Для данной матрицы  : :  . Тогда . Тогда 
и

 . .
Ответ :  . .
2) Найти неизвестную матрицу  из уравнения из уравнения
 . .
Решение.
Исходное уравнение запишем в матричной форме
 , где , где  , ,  . .
Матричное уравнение вида  имеет решение, если матрицы имеет решение, если матрицы  и и  – квадратные матрицы одинакового порядка и – квадратные матрицы одинакового порядка и  , т.е. для матрицы , т.е. для матрицы  существует обратная матрица существует обратная матрица  . Умножая справа обе части уравнения . Умножая справа обе части уравнения  на на  , получим , получим  , где , где  единичная матрица, или единичная матрица, или  , или , или
 искомая матрица. искомая матрица.
Для данной матрицы  : :  . Следовательно, существует . Следовательно, существует  . Найдем ее по формуле, указанной в примере 1), имеем . Найдем ее по формуле, указанной в примере 1), имеем  и и
 . .
Тогда

 . .
Ответ :  . .
4. Решить систему линейных уравнений методом Крамера.
Дана система уравнений:
  . .
Решение.
Решение системы находим по формулам Крамера
 . .
Для начала вычислим определитель системы
Обозначим через  определитель матрицы определитель матрицы  . Пусть . Пусть  есть определитель матрицы есть определитель матрицы  , в которой вместо первого столбца стоит столбец , в которой вместо первого столбца стоит столбец  . Пусть . Пусть  есть определитель матрицы есть определитель матрицы  , в которой вместо второго столбца стоит столбец , в которой вместо второго столбца стоит столбец  . Наконец, пусть . Наконец, пусть  есть определитель матрицы есть определитель матрицы  , в которой вместо третьего столбца стоит столбец , в которой вместо третьего столбца стоит столбец  . .
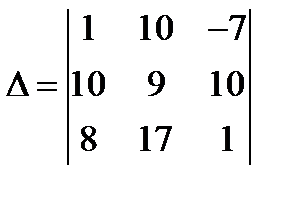 , ,
 , ,  , , 
Если  , то согласно правилу Крамера решение системы уравнений можно найти по формулам , то согласно правилу Крамера решение системы уравнений можно найти по формулам
 , ,  , ,  . .
Имеем:
 
 
 
Следовательно, по формулам Крамера,
 , ,  , ,  . .
5. Решить систему уравнений с помощью обратной матрицы.
Решим теперь ту же систему уравнений матричным способом, с вычислением обратной матрицы.
Запишем ту же систему линейных уравнений в матричной форме: 
где

Поскольку по определению обратной матрицы  имеем имеем
 Û Û  , ,
и так как  , решение системы можно записать в виде , решение системы можно записать в виде
 . .
Чтобы находить  , необходимо научиться вычислять определитель , необходимо научиться вычислять определитель  матрицы матрицы  . .
Нам понадобятся два понятия: знак элемента матрицы и минор элемента. Для элемента  , стоящего в , стоящего в  –й строке, –й строке,  –м столбце матрицы –м столбце матрицы  , знак , знак  равен числу равен числу  . Удобно использовать следующее правило знакочередования: у элемента . Удобно использовать следующее правило знакочередования: у элемента  первой строки, первого столбца знак равен первой строки, первого столбца знак равен  , а у любых двух соседних по строке или столбцу элементов знаки различны. , а у любых двух соседних по строке или столбцу элементов знаки различны.

Минором  элемента элемента  называется определитель матрицы, которая получается вычеркиванием называется определитель матрицы, которая получается вычеркиванием  -й строки и -й строки и  –го столбца исходной матрицы –го столбца исходной матрицы  . .
Определение определителя матриц начнем с матриц размера  . Определитель матрицы размера . Определитель матрицы размера  равен произведению элементов главной диагонали (то есть диагонали, идущей сверху вниз и слева направо) минус произведение элементов сопряженной диагонали, равен произведению элементов главной диагонали (то есть диагонали, идущей сверху вниз и слева направо) минус произведение элементов сопряженной диагонали,
 . .
В частности,  . .
Определитель матрицы размера  сводится к вычислению трех определителей матриц размера сводится к вычислению трех определителей матриц размера  по следующему правилу: надо выделить произвольную строку (или столбец) матрицы по следующему правилу: надо выделить произвольную строку (или столбец) матрицы  , умножить каждый элемент этой строки (столбца) на знак этого элемента, и умножить на минор элемента, а затем все полученные произведения сложить. Это правило называется разложением определителя по строке (столбцу). Можно показать, что результат не зависит от выбора строки или столбца. , умножить каждый элемент этой строки (столбца) на знак этого элемента, и умножить на минор элемента, а затем все полученные произведения сложить. Это правило называется разложением определителя по строке (столбцу). Можно показать, что результат не зависит от выбора строки или столбца.
Приведем результат разложения определителя матрицы  по первой строке: по первой строке:

В частном случае:


Поскольку  , обратная матрица , обратная матрица  существует. Для вычисления существует. Для вычисления  используем формулу используем формулу
 , ,
где  – алгебраические дополнения элементов – алгебраические дополнения элементов  матрицы матрицы  (заметим, что алгебраические дополнения элементов строк записываются в соответствующие столбцы). Получаем: (заметим, что алгебраические дополнения элементов строк записываются в соответствующие столбцы). Получаем:
 , ,  , , 
 , , 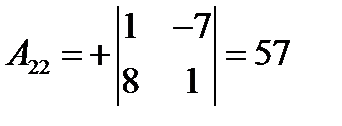 , ,  , ,
 , ,  , ,  . .
Обратная матрица, следовательно, имеет вид

Остается умножить матрицу  на столбец на столбец  , ,
 
Ответы совпали.
6. Решить систему методом Гаусса.
Рассмотрим ту же систему уравнений:

Решение.
Сначала нужно преобразовать систему уравнений так, чтобы переменная  осталась только в одном уравнении системы, например, в первом. Затем уравнение, в которое входит осталась только в одном уравнении системы, например, в первом. Затем уравнение, в которое входит  , отбрасывают, и рассматривают систему из оставшихся уравнений, в котором число уравнений и число неизвестных уменьшилось. Эту редуцированную систему преобразуют так, чтобы переменная , отбрасывают, и рассматривают систему из оставшихся уравнений, в котором число уравнений и число неизвестных уменьшилось. Эту редуцированную систему преобразуют так, чтобы переменная  осталась только в одном уравнении. Затем уравнение, в которое входит осталась только в одном уравнении. Затем уравнение, в которое входит  , отбрасывают, и вновь рассматривают систему из меньшего числа уравнений. Преобразования с последовательным исключением неизвестных , отбрасывают, и вновь рассматривают систему из меньшего числа уравнений. Преобразования с последовательным исключением неизвестных  , ,  , ,  и т.д. продолжают до тех пор, пока к каждой неизвестной не будет применена процедура исключения. После этого значения и т.д. продолжают до тех пор, пока к каждой неизвестной не будет применена процедура исключения. После этого значения  , ,  , ,  ,… определяют сначала из последнего уравнения, затем из предпоследнего и т.д., вплоть до первого уравнения. ,… определяют сначала из последнего уравнения, затем из предпоследнего и т.д., вплоть до первого уравнения.
Итак, возьмем первое уравнение системы и с его помощью исключим переменную  из второго и третьего уравнений. Для этого первое уравнение перепишем без изменений, а второе и третье уравнения сложим с подходящими коэффициентами с первым уравнений системы. Сначала умножим первое уравнение системы на 10, второе - на из второго и третьего уравнений. Для этого первое уравнение перепишем без изменений, а второе и третье уравнения сложим с подходящими коэффициентами с первым уравнений системы. Сначала умножим первое уравнение системы на 10, второе - на  , а затем сложим полученные уравнения. Получим , а затем сложим полученные уравнения. Получим

Аналогично, умножим первое уравнение системы на 8, второе - на  , а затем сложим. , а затем сложим.

Данное преобразование будем записывать в следующем виде:
 Û Û 
Возьмем теперь второе уравнение и с его помощью исключим переменную  из третьего уравнения системы. Для этого второе уравнение системы умножим на 63, третье уравнение умножим на из третьего уравнения системы. Для этого второе уравнение системы умножим на 63, третье уравнение умножим на  , и сложим полученные уравнения. , и сложим полученные уравнения.
 Û Û 
Мы привели систему уравнений к так называемому верхне-треугольному виду. Теперь методом обратного хода можно определить сначала значение переменной  из последнего уравнения системы, затем значение переменной из последнего уравнения системы, затем значение переменной  из второго уравнения, и, наконец, значение переменной из второго уравнения, и, наконец, значение переменной  из первого уравнения. из первого уравнения.



Ответ: тот же -  . .
7. Найти общее решение однородной системы линейных алгебраических уравнений  . .
Решение.
Элементарными преобразованиями строк приведем матрицу системы  к эквивалентной матрице к эквивалентной матрице  , которой соответствует уравнение , которой соответствует уравнение  , эквивалентное исходной системе. Таким образом, общее решение может быть записано в форме , эквивалентное исходной системе. Таким образом, общее решение может быть записано в форме  , или , или  , ,  . Решений бесчисленное множество – любая пара, связанная указанной зависимостью, обращает левые части уравнений данной системы в нуль. В системе . Решений бесчисленное множество – любая пара, связанная указанной зависимостью, обращает левые части уравнений данной системы в нуль. В системе  - число неизвестных и число уравнений. - число неизвестных и число уравнений.  , ,  матрица системы, матрица системы,  расширенная матрица системы. В силу теоремы Кронекера-Капелли система имеет бесчисленное множество решений, зависящих от одного параметра расширенная матрица системы. В силу теоремы Кронекера-Капелли система имеет бесчисленное множество решений, зависящих от одного параметра  . Иногда общее решение удобнее использовать в форме . Иногда общее решение удобнее использовать в форме
 . .
8. При каких значениях  система система

имеет нетривиальные (ненулевые) решения ? Найти эти решения.
Решение.
Однородная система линейных уравнений имеет ненулевые решения, когда ее определитель равен нулю. Из этого условия и найдем соответствующие значения  : :
 . .
Найдем теперь соответствующие решения.
1) При  система имеет вид : система имеет вид :
 . .
Определитель этой системы равен нулю. Это означает наличие линейной зависимости между уравнениями системы. Замечаем, что первое уравнение получается из второго и поэтому его можно отбросить. Имеем
 . .
Так как определитель из коэффициентов при неизвестных  не равен нулю, то в качестве базисных неизвестных возьмем не равен нулю, то в качестве базисных неизвестных возьмем  (хотя можно брать и другие пары неизвестных) и перенесем члены с (хотя можно брать и другие пары неизвестных) и перенесем члены с  в правые части уравнений : в правые части уравнений :
 . .
Полученную систему можно решить по формулам Крамера :

где  , ,  , ,  . .
Тогда  , ,  . Полагая . Полагая  , где , где  произвольное действительное число , получаем решение системы : произвольное действительное число , получаем решение системы :  , , 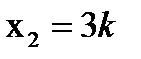 , ,  . .
2) При  система имеет вид : система имеет вид :
 . .
Можно решить эту систему и методом Гаусса. Составим расширенную матрицу  полученной системы : полученной системы :
 и приведем ее к матрице ступенчатого вида : и приведем ее к матрице ступенчатого вида :

  . .
Восстановим систему для полученной матрицы
   
   . .
Полагая  , где , где  произвольное действительное число, получаем решение системы : произвольное действительное число, получаем решение системы :  . .
Ответ : При  система имеет нетривиальные решения : система имеет нетривиальные решения :  , ,  , ,  , ,  . При . При  система имеет нетривиальные решения : система имеет нетривиальные решения :  , ,  . .
Индивидуальные задания
Вариант № 1
1.1.  1.2. 1.2. 
1.3. 
1.4.-1.6.  1.7. 1.7.  1.8. 1.8. 
Вариант № 2
2.1. 
2.2. 
2.3. 
2.4. – 2.6. 
2.7.  2.8. 2.8. 
Вариант № 3
3.1 
3.2. 
3.3. 
3.4. -3.6. 
3.7.  3.8. 3.8.  . .
Вариант № 4
4. 1. 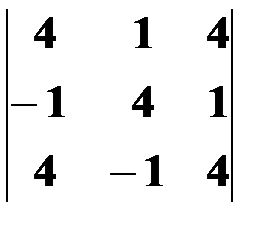
4.2. 
4.3. 
4.4. – 4.6. 
4.7.  4.8. 4.8.  . .
Вариант № 5
5.1. 
5.2. 
5.3. 
5.4. – 5.6. 
5.7.  5.8. 5.8.  . .
Вариант № 6
6.1. 
6.2. 
6.3. 
6.4. -6.6. 
6.7. 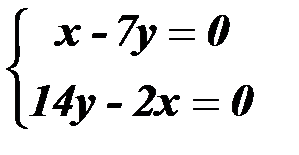 6.8. 6.8. 
Вариант № 7
7.1. 
7.2. 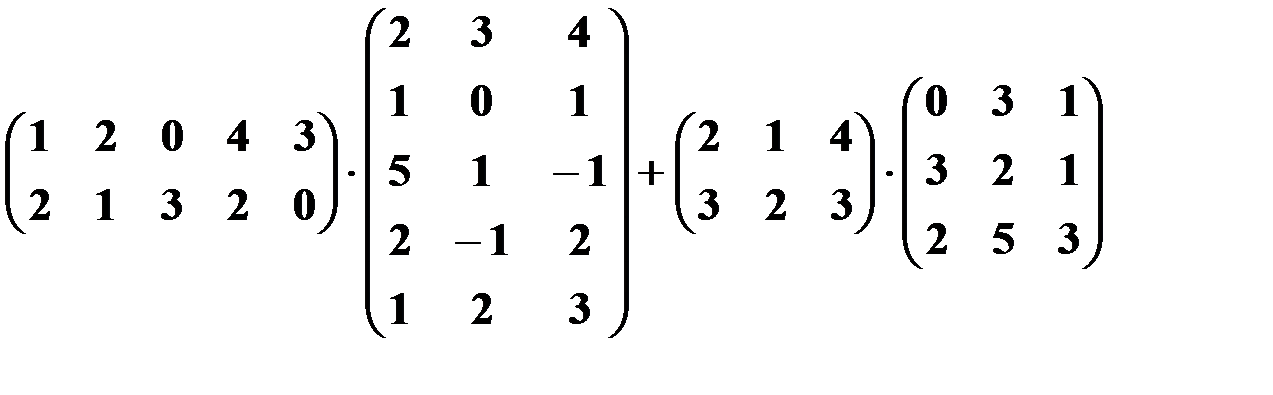
7.3. 
7.4. -7.6. 
7.7. 
7. 6. 
Вариант № 8
8.1. 
8.2. 
8.3. 
8.4. -8.6. 
8.7.  8.8. 8.8.  . .
Вариант № 9
9.1. 
9.2. 
9.3. 
9.4. -9.6. 
9.7.  9.8. 9.8.  . .
Вариант № 10
10.1. 
10.2. 
10.3. 
10.4. -10.6. 
10.7.  10.8. 10.8.  . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , где
, где  ,
,  .
. имеет решение, если матрицы
имеет решение, если матрицы  и
и  – квадратные матрицы одинакового порядка и матрица
– квадратные матрицы одинакового порядка и матрица  . В этом случае для матрицы
. В этом случае для матрицы  . Умножая слева обе части уравнения
. Умножая слева обе части уравнения  , где
, где  единичная матрица,
единичная матрица, искомая матрица.
искомая матрица. :
:  . Следовательно, существует
. Следовательно, существует  . Найдем ее по формуле
. Найдем ее по формуле 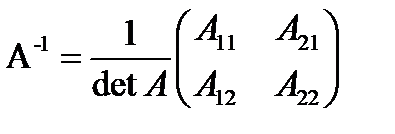 , где
, где  алгебраическое дополнение элемента
алгебраическое дополнение элемента  матрицы
матрицы  . Для данной матрицы
. Для данной матрицы  :
:  . Тогда
. Тогда 

 .
. .
. из уравнения
из уравнения .
. , где
, где  ,
,  .
. имеет решение, если матрицы
имеет решение, если матрицы  , т.е. для матрицы
, т.е. для матрицы  на
на  , где
, где  единичная матрица, или
единичная матрица, или  , или
, или искомая матрица.
искомая матрица. . Следовательно, существует
. Следовательно, существует  и
и .
.
 .
. .
.
 .
. .
. определитель матрицы
определитель матрицы  . Пусть
. Пусть  есть определитель матрицы
есть определитель матрицы  . Пусть
. Пусть  есть определитель матрицы
есть определитель матрицы  , в которой вместо второго столбца стоит столбец
, в которой вместо второго столбца стоит столбец  есть определитель матрицы
есть определитель матрицы  , в которой вместо третьего столбца стоит столбец
, в которой вместо третьего столбца стоит столбец 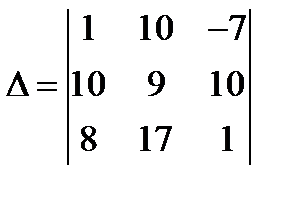 ,
, ,
,  ,
, 
 , то согласно правилу Крамера решение системы уравнений можно найти по формулам
, то согласно правилу Крамера решение системы уравнений можно найти по формулам ,
,  ,
,  .
.





 ,
,  ,
,  .
.

 имеем
имеем Û
Û  ,
, , решение системы можно записать в виде
, решение системы можно записать в виде .
. матрицы
матрицы  , стоящего в
, стоящего в  –й строке,
–й строке,  –м столбце матрицы
–м столбце матрицы  . Удобно использовать следующее правило знакочередования: у элемента
. Удобно использовать следующее правило знакочередования: у элемента  первой строки, первого столбца знак равен
первой строки, первого столбца знак равен  , а у любых двух соседних по строке или столбцу элементов знаки различны.
, а у любых двух соседних по строке или столбцу элементов знаки различны.
 элемента
элемента  называется определитель матрицы, которая получается вычеркиванием
называется определитель матрицы, которая получается вычеркиванием  . Определитель матрицы размера
. Определитель матрицы размера  .
. .
. сводится к вычислению трех определителей матриц размера
сводится к вычислению трех определителей матриц размера  по следующему правилу: надо выделить произвольную строку (или столбец) матрицы
по следующему правилу: надо выделить произвольную строку (или столбец) матрицы  по первой строке:
по первой строке:


 , обратная матрица
, обратная матрица  существует. Для вычисления
существует. Для вычисления  ,
, – алгебраические дополнения элементов
– алгебраические дополнения элементов  ,
,  ,
, 
 ,
, 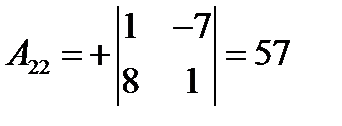 ,
,  ,
, ,
,  ,
,  .
.
 ,
,

 осталась только в одном уравнении системы, например, в первом. Затем уравнение, в которое входит
осталась только в одном уравнении системы, например, в первом. Затем уравнение, в которое входит  осталась только в одном уравнении. Затем уравнение, в которое входит
осталась только в одном уравнении. Затем уравнение, в которое входит  и т.д. продолжают до тех пор, пока к каждой неизвестной не будет применена процедура исключения. После этого значения
и т.д. продолжают до тех пор, пока к каждой неизвестной не будет применена процедура исключения. После этого значения  , а затем сложим полученные уравнения. Получим
, а затем сложим полученные уравнения. Получим

 Û
Û 
 , и сложим полученные уравнения.
, и сложим полученные уравнения. Û
Û 
 из второго уравнения, и, наконец, значение переменной
из второго уравнения, и, наконец, значение переменной 


 .
. .
. к эквивалентной матрице
к эквивалентной матрице  , которой соответствует уравнение
, которой соответствует уравнение  , эквивалентное исходной системе. Таким образом, общее решение может быть записано в форме
, эквивалентное исходной системе. Таким образом, общее решение может быть записано в форме  , или
, или  ,
,  . Решений бесчисленное множество – любая пара, связанная указанной зависимостью, обращает левые части уравнений данной системы в нуль. В системе
. Решений бесчисленное множество – любая пара, связанная указанной зависимостью, обращает левые части уравнений данной системы в нуль. В системе  - число неизвестных и число уравнений.
- число неизвестных и число уравнений.  ,
,  матрица системы,
матрица системы,  расширенная матрица системы. В силу теоремы Кронекера-Капелли система имеет бесчисленное множество решений, зависящих от одного параметра
расширенная матрица системы. В силу теоремы Кронекера-Капелли система имеет бесчисленное множество решений, зависящих от одного параметра  . Иногда общее решение удобнее использовать в форме
. Иногда общее решение удобнее использовать в форме .
. система
система
 .
. система имеет вид :
система имеет вид : .
. .
. не равен нулю, то в качестве базисных неизвестных возьмем
не равен нулю, то в качестве базисных неизвестных возьмем  в правые части уравнений :
в правые части уравнений : .
.
 ,
,  ,
,  .
. ,
,  . Полагая
. Полагая  , где
, где  произвольное действительное число , получаем решение системы :
произвольное действительное число , получаем решение системы :  ,
, 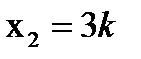 ,
,  .
. система имеет вид :
система имеет вид : .
. полученной системы :
полученной системы : и приведем ее к матрице ступенчатого вида :
и приведем ее к матрице ступенчатого вида :

 .
.





 .
. , где
, где  произвольное действительное число, получаем решение системы :
произвольное действительное число, получаем решение системы :  .
. система имеет нетривиальные решения :
система имеет нетривиальные решения :  ,
,  ,
,  ,
,  . При
. При  система имеет нетривиальные решения :
система имеет нетривиальные решения :  ,
,  .
. 1.2.
1.2. 

 1.7.
1.7.  1.8.
1.8. 




 2.8.
2.8. 




 3.8.
3.8.  .
.



 4.8.
4.8.  .
.



 5.8.
5.8.  .
.



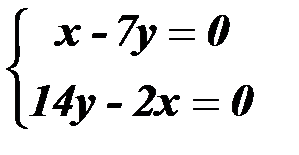 6.8.
6.8. 









 8.8.
8.8.  .
.



 9.8.
9.8.  .
.



 10.8.
10.8.  .
.