
|
|
Измерений (косвенные измерения)К.В. Подмастерьев, Е.В. Пахолкин, В.В. Мишин
МЕТОДИЧЕСКИЕ УКАЗАНИЯ По выполнению расчетно-графических И курсовых работ по метрологическим дисциплинам Орел 2016 г. вторы: заведующий кафедрой ПМиС, доктор технических наук, профессорК.В. Подмастерьев професор кафедры ПМиС, кандидат технических наук Е.В. Пахолкин професор кафедры ПМиС, кандидат технических наукВ.В. Мишин
Рецензент: доцент кафедры ПМиС,кандидат технических наук, доцент З.П. Лисовская
Методические указания по выполнению расчетно-графических и курсовых работ по метрологическим дисциплинам содержат задания по обработке экспериментальных данных при выполнении однократных и многократных измерений, нескольких серий измерений, при функциональных преобразованиях результатов измерений и исследовании физических зависимостей. В настоящих методических указаниях представлены индивидуальные задания пяти видов (по 100 вариантов).
Редактор Т.Д Васильева Технический редактор <инициалы, фамилия>
Подписано к печати <дата>. Формат 60x84 1/16. Печать офсетная. Уч.-изд.л. 2,3. Усл. печ. л. _____.. Тираж 100 экз. Заказ № <число> Отпечатано с готового оригинал-макета на полиграфической базе ОрелГТУ,
302020, г. Орел, ул. Московская, 65.
Ó ФГБОУ !ПГУ», 2016 Подмастерьев К.В., Пахолкин Е.В., Мишин В.В., 2016
Содержание
ОБЩИЕ ПОЛОЖЕНИЯ Содержание расчетно-графической работы
Согласно государственным образовательным стандартам циклы общепрофессиональных дисциплин практически по любой специальности включают одну из метрологических дисциплин. Например, по специальности 190100 изучается дисциплина «Метрология, стандартизация, сертификация», по специальностям 220500 и 200800 – «Метрология, стандартизация и технические измерения». При этом рабочие планы для различных специальностей предполагают выполнение расчетно-графических или курсовых работ. Наряду со специфическими задачами изучения метрологической дисциплины для каждой специальности есть общие цели и задачи для всех специальностей. Одной из основных задач изучения метрологических дисциплин в вузе является освоение методов получения достоверной измерительной информации и правильного ее использования, а также приобретение практических навыков обработки данных при выполнении различных видов измерений. Решению указанной задачи и служат задания, изложенные в данных методических указаниях. При выполнении работы студент углубляет теоретические знания и получает практические навыки в области обработки экспериментальных данных при выполнении однократных и многократных измерений, нескольких серий измерений, при функциональных преобразованиях результатов измерений и исследовании физических зависимостей. В настоящих методических указаниях представлены индивидуальные задания пяти видов (по сто вариантов): – задание 1. Однократное измерение; – задание 2. Многократное измерение; – задание 3. Обработка результатов нескольких серий измерений; – задание 4. Функциональные преобразования результатов измерений; – задание 5. Обработка экспериментальных данных при изучении зависимостей. В зависимости от изучаемой дисциплины и планируемого объема работа может включать лишь некоторые из представленных пяти заданий.
Оформление работы
Расчетно-графические и курсовые работы оформляются на листах стандартного формата А4 (297x210 мм). Форма титульного листа представлена в приложении А. Работа должна включать по каждому заданию: условие задачи; экспериментальные данные; априорную информацию; выбранный алгоритм обработки с соответствующими пояснениями и промежуточные результаты обработки экспериментальных данных; полученный результат измерений; необходимые графики и диаграммы, поясняющие решение задач. В конце работы необходимо представить список использованных источников. ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ Задание 1. Однократное измерение 2.1.1 Условие задания При однократном измерении физической величины получено показание средства измерения X = 10. Определить, чему равно значение измеряемой величины, если экспериментатор обладает априорной информацией о средстве измерений и условиях выполнения измерений согласно данным таблицы 1. Указания по выполнению 1. Исходные данные студент выбирает из таблицы 1 по предпоследней и последней цифрам шифра; например шифру 96836 соответствует априорная информация, определяемая на пересечении строки 3 столбца 6. 2. Априорная информация в таблице 1 представлена в двух вариантах. В первом варианте даются сведения о классе точности средства измерений: пределы измерений, класс точности, значение аддитивной (qа) или мультипликативной (qм) поправки. Например, данные: -50...50; 1,5; qа = 0,5, – означают, что средство измерения имеет диапазон измерений от -50 до 50, класс точности 1,5, а значение аддитивной поправки равняется 0,5. Во втором варианте в качестве априорной информации даются сведения о видах и характеристиках распределения вероятности результата измерения: вид закона распределения, значение оценки среднего квадратического отклонения (Sx), доверительная вероятность Р (для нормального закона распределения) и значение аддитивной (qа) или мультипликативной (qм) поправки. Например, данные: норм.; Sx =0,5; Р = 0,95; qм = 1,1 – означают, что закон распределения вероятности результата измерения нормальный, со значением оценки среднеквадратического отклонения 0,5. При этом имеет место мультипликативная поправка (поправочный множитель) 1,1, а доверительный интервал следует рассчитывать с доверительной вероятностью 0,95. Порядок расчета Результат измерения при однократном измерении определяется по алгоритму, представленному на рисунке 34 в источнике [1]. Обработка экспериментальных данных зависит от вида используемой априорной информации. Если это информация о классе точности, то пределы, в которых находится значение измеряемой величины без учета поправки, определяются следующим образом:
Q1 = X – DХ; Q2 = X + DХ,
где DХ - предел допускаемой абсолютной погрешности средства измерения при его показании X. Значение DХ определяется в зависимости от класса точности и способа его задания по ГОСТ 8.401-80. Если в качестве априорной используется информация о законе распределения вероятности, то пределы определяются через доверительный интервал:
Q1 = X – E; Q2 = X + Е.
Значение Е определяется в зависимости от вида закона распределения вероятности результата измерения. Для нормального закона
Е = t∙Sx,
где t для заданной доверительной вероятности Р выбирается из таблиц интегральной функции нормированного нормального распределения Ф(t) (например, табл. 1.1.2.6.2 [2], при этом следует учитывать, что Р = 2Ф(t)). Таблица распределения также приведена в приложении Б. Для равномерного закона распределения вероятности результата измерения значение Е (аналог доверительного интервала) можно определить из выражения
Е = a∙Sx,
где При представлении результата измерения необходимо внести поправки и уточнить пределы, в которых находится значение измеряемой величины. При вычислении следует руководствоваться правилами округления, согласно которым значения среднеквадратических отклонений указываются в окончательном ответе двумя значащими цифрами, если первая из них равна 1 или 2, и одной, если первая равна 3 или более. Все предварительные расчеты выполняются не менее чем с одним или двумя лишними знаками. В качестве справочных данных могут использоваться аналогичные таблицы из других литературных источников.
Задание 2. Многократное измерение
2.2.1 Условие задания При многократном измерении одной и той жефизической величины получена серия из 24 результатов измерений Qi; i Î [1...24]. Эти результаты после внесения поправок представлены в таблице 2. Определить результат измерения.
Таблица 2 – Исходные данные
Указания по выполнению 1. Серию экспериментальных данных студент выбирает из таблицы 2 по предпоследней и последней цифрам шифра. Например, шифру 96836 соответствует серия, включающая все результаты измерений, которые приведены в строке 3 и столбце 6. 2. Результат измерения следует получить с доверительной вероятностью 0,95. Порядок расчета Результат многократного измерения находится по алгоритму, представленному на рисунке 40 [1]. При этом необходимо учитывать, что n = 24, следовательно, порядок расчетов и их содержание определяются условием 10…15 < n < 40…50. 1. Определить точечные оценки результата измерения: среднего арифметического 2. Обнаружить и исключить ошибки. Для этого необходимо: – вычислить наибольшее по абсолютному значению нормированное отклонение
– задаться доверительной вероятностью Р и из соответствующих таблиц (таблица П.6 [3] или из таблица В.1) с учетом q = 1 – Р найти соответствующее ей теоретическое (табличное) значение νq; – сравнить ν с νq. Если ν > νq, то данный результат измерения Qi является ошибочным, он должен быть отброшен. После этого необходимо повторить вычисления по пунктам 1 и 2 для сокращенной серии результатов измерений. Вычисления проводятся до тех пор, пока не будет выполняться условие ν < νq. 3. Проверить гипотезу о нормальности распределения оставшихся результатов измерений. Проверка выполняется по составному критерию [3]. Применив критерий 1, следует: – вычислить отношение
– задаться доверительной вероятностью P1 (рекомендуется принять P1 = 0,98) и для уровня значимости q1 = 1 – Р1 по соответствующим таблицам (таблица П.7 [3] или таблица Г.1) определить квантили распределения d1-0,5ql ,и d0,5q1; – сравнить d с d1-0,5ql и d0,5q1. Если d1-0,5q1 < d < d0,5q1, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными. Применив критерий 2, следует: – задаться доверительной вероятностью Р2 (рекомендуется принять Р2 = 0,98) и для уровня значимости q2 = 1 – Р2 с учетом n определить по соответствующим таблицам (таблица П.8 [3] или таблица Г.2) значения m и Р*; – для вероятности Р* из таблиц для интегральной функции нормированного нормального распределения Ф(t) (таблица 1.1.2.6.2 [2] или таблица Б.1) определить значение t и рассчитать Е = t∙SQ. Если не более m разностей | Если хотя бы один из критериев не соблюдается, то гипотезу о нормальности распределения отвергают. 4. Определить стандартное отклонение среднего арифметического. Если закон распределения вероятности результата измерений признан нормальным, то стандартное отклонение определяют как Если гипотеза о нормальности распределения отвергается, то
5. Определить доверительный интервал. Если закон распределения вероятности результата измерений признан нормальным, то доверительный интервал для заданной доверительной вероятности Р определяется из распределения Стьюдента Е = t×S, где t выбирается из соответствующих таблиц (таблица 1.1.2.8 [2] или таблица Д.1, при этом m = n – 1, а a = Р). Если гипотеза о нормальности распределения отвергается, то t определяется из неравенства П. Л. Чебышева:
Р ³ 1 – 1/t2.
Задание3. Обработка результатов нескольких серий измерений
2.3.1 Условие задания При многократных измерениях одной и той же величины получены две серии по 12 (nj) результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице 2. Вычислить результат многократных измерений. Указания по выполнению 1. Серии в таблице 2 студент выбирает по предпоследней и последней цифрам шифра: например, шифру 96836 соответствуют все результаты измерений, которые приведены в строке 3 (серия 1) и столбце 6 (серия 2). 2. Результат измерения следует получить с достоверностью 0,95. Порядок расчета Обработку результатов двух серий измерений целесообразно осуществлять по алгоритмам [1, с. 122-129] (последовательность расчетов и их содержание определяются условием 10...15 < n < 40...50). 1. Обработать экспериментальные данные в каждой j-й серии отдельно по алгоритму, изложенному в задании 2 (алгоритм обработки многократных измерений), при этом: – определить оценки результата измерения Qj и среднего квадратического отклонения sqj; – обнаружить и исключить ошибки; – проверить гипотезу о нормальности распределения оставшихся результатов измерений. 2. Проверить значимость различия средних арифметических серий по алгоритму, представленному на рисунке 48 [1]. Для этого следует: – вычислить моменты закона распределения разности:
G =
– задавшись доверительной вероятностью Р, определить из соответствующих таблиц интегральной функции нормированного нормального распределения Ф(t) (таблица 1.1.2.6.2 [2] или таблица Б.1) значение t; – сравнить |G| с t × Sg. Если |G| 3. Проверить равнорассеянность результатов измерений в сериях по алгоритму, изложенному на рисунке 50 [1]. Для этого необходимо: – определить значение – задавшись доверительной вероятностью Р, определить из соответствующих таблиц (таблица 16 [1] или таблица Е.1) значение аргумента интегральной функции распределения вероятности Фишера y0; – сравнить y с y0. Если y < y0, то серии с доверительной вероятностью Р считают рассеянными. 4. Обработать совместно результаты измерения обеих серий с учетом того, однородны серии или нет. Если серии однородны (равнорассеянны с незначимым различием средних арифметических), то все результаты измерения следует объединить в единый массив и выполнить обработку по алгоритму на рисунке 40 [1]. Для этого необходимо: – определить оценку результата измерения
– задавшись доверительной вероятностью Р, определить из таблиц распределения Стьюдента (таблица 1.1.2.8 [2] или таблица Д.1) значение t для числа степеней свободы – определить доверительный интервал Е = t×S. Если серии не равнорассеянны с незначимым различием средних арифметических, то совместную обработку результатов измерений следует выполнять с учетом весовых коэффициентов по алгоритму, представленному на рисунке 51 [1]. Для этого необходимо: – определить оценки результата измерения –
– аналогично предыдущему случаю, задавшись доверительной вероятностью Р, определить t и доверительный интервал. Если различие средних арифметических в сериях признано значимым, то результаты измерений в каждой серии следует обработать раздельно по алгоритму многократных измерений: – в зависимости от закона распределения вероятности результата измерения в каждой серии определить Sj; – задавшись доверительной вероятностью Р, определить по соответствующим таблицам значение tj; – рассчитать доверительный интервал Еj =Sj × tj.
Задание 4. Функциональные преобразования результатов измерений (косвенные измерения)
2.4.1 Условие задания При многократных измерениях независимых величин X и У получено по 12 (n) результатов измерений. Эти результаты после внесения поправок представлены в таблице 2. Определить результат вычисления Z = f (X,У), (вид функции Z и характер величин X, У, Z представлены в таблице 3). Указания по выполнению 1. Значения X и У студент выбирает, соответственно, по предпоследней и последней цифрам шифра: например, шифру 96836 соответствуют значения X, представленные в строке 3 и значения У, представленные в столбце 6 таблицы 2. 2. Вид функции Z студент выбирает по последней цифре шифра, например, шифру 96836 соответствует функция Z, представленная в строке 6 таблицы 3. 3. При определении Z следует предварительно выразить значения величин X и У в единицах системы СИ. Порядок расчетa Обработку экспериментальных данных при функциональном преобразовании результатов измерений целесообразно осуществлять по алгоритму [1, с. 144 – 166]. При этом необходимо учитывать, что n = 12, следовательно, порядок расчетов и их содержание определяются условием 10...15 < n < 40...50. 1. Обработать результаты измерений величин X и У отдельно по алгоритму, изложенному в п. п. 1-3 задания 2, при этом: – определить оценки результатов измерений X, У и средних квадратических отклонений Sx, Sy; – обнаружить и исключить ошибки; – проверить гипотезу о нормальности распределения оставшихся результатов измерений. 2. Определить оценку среднего значения функции:
3. Определить поправку:
Таблица 3 – Исходные данные
4. Определить оценку стандартного отклонения функции
где nx, ny – числа оставшихся результатов измерений, соответственно, X и Упосле исключения ошибок. 5. Определить доверительный интервал для функции
ЕZ = t×S.
Если законы распределения вероятности результатов измерения X и У признаны нормальными, то t можно определить для принятой доверительной вероятности Р из таблиц для распределения Стьюдента (таблица 1.1.2.8 [2] или таблица Д.1). При этом число степеней свободы m определятся из выражения
Если гипотеза о нормальности распределения результатов измерения X или (и) У отвергается, то t целесообразно определить из неравенства Чебышева:
Задание 5. Обработка экспериментальных данных при Изучении зависимостей
2.5.1 Условие задания При многократных совместных измерениях величин X и Y получено по 20 (n) пар результатов измерений. Эти результаты после внесения поправок представлены в таблице 4. Определить уравнение регрессии Y по X: Y = f (X). Указания по выполнению 1. Серии экспериментальных данных студент выбирает из таблице 4 по предпоследней и последней цифрам шифра. Например, шифру 96836 соответствуют серии, включающие все результаты измерений X (числитель) и У (знаменатель), которые представлены в строке 3 и столбце 6. 2. Считать, что результаты измерений не содержат ошибок. 2.5.3 Порядок расчета Обработку экспериментальных данных при изучении зависимостей целесообразно осуществлять по алгоритмам [4, с. 99-109]. 1. В осях координат X и Y построить n экспериментальных точек с координатами Xi ,Yi, i Î (1…20) и по характеру расположения точек принять гипотезу о виде уравнения регрессии Y на X.
Таблица 4 – Исходные данные
В качестве уравнения регрессии целесообразно использовать полином степени m:
Y = А + В∙Х + С∙Х2 + ... + К∙Хm.
В первом приближении для решения данной задачи рекомендуется принять m = 1, т.е.
Y = А + В∙Х.
2 Определить параметры уравнения регрессии по методу наименьших квадратов. Для этого необходимо: – составить систему уравнений по числу рассчитываемых параметров:
где Например, для линейного уравнения регрессии система уравнений имеет вид:
– решить систему уравнений и определить неизвестные параметры, например, для линейного уравнения регрессии решение имеет вид:
3. Проверить правильность выбора вида уравнения регрессии. Для этого следует применить непараметрические критерии серий и инверсий: – рассчитать отклонения экспериментальных значений Yi от соответствующих значений Ypi, рассчитанных для того же аргумента Xi по полученному уравнению регрессии:
DYi = Yi – Ypi ;
– построить в осях координат X, DY полученные значения DYi для соответствующих Xi; – записать последовательность значений DYj по мере возрастания Xj, Xj Î [l,n]; – рассчитать число серий N в полученной последовательности DYj (под серией в данном случае понимают последовательность отклонений одного знака, перед и после которой следуют отклонения противоположного знака или нет вообще никаких отклонений); – задавшись доверительной вероятностью Р ( уровнем значимости a = 1 – Р) для n = 20 определить по соответствующей таблице (таблица А.6 [4] или таблица Ж.1) допустимые границы N1-0,5a и N0,5a; – рассчитать число инверсий А в полученной последовательности DYj (под инверсией понимается событие, заключающееся в том, что DYj > DYjk при k > j):
где Aj – это число инверсий j - гo члена последовательности, т.е. число членов последовательности, которые, будучи расположенными в последовательности после j - ого члена, имеют значение меньшее, чем DYj; – задавшись доверительной вероятностью Р ( уровнем значимости a = 1 – Р) для n = 20 определить по соответствующей таблице (таблица А.7 [4] или таблица И.1) допустимые границы A1-0,5a и A0,5a; – сравнить А с A1-0,5a и A0,5a; Если выполняются неравенства
N1-0,5a < N £ N0,5a; A1-0,5a < A £ A0,5a,
то с выбранной доверительной вероятностью Р можно считать, что отклонения экспериментальных значений Yi, от соответствующих значений Yрi найденного уравнения регрессии являются случайными, не содержат аддитивного, мультипликативного или колебательного трендов, т.е. рассчитанное уравнение регрессии достоверно описывает экспериментально исследуемую зависимость между величинами X и Y. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. и среднего квадратического отклонения SQ результата измерения.
и среднего квадратического отклонения SQ результата измерения. ;
;
 i -
i -  | превосходит Е, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными, закон можно признать нормальным с вероятностью Р0 ³ (Р1 + Р2 – 1).
| превосходит Е, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными, закон можно признать нормальным с вероятностью Р0 ³ (Р1 + Р2 – 1). .
. .
.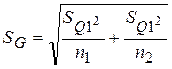 ;
; t · Sg, то различие между средними арифметическими в сериях с доверительной вероятностью Р можно признать незначимым.
t · Sg, то различие между средними арифметическими в сериях с доверительной вероятностью Р можно признать незначимым. ;
; и среднего квадратического отклонения S:
и среднего квадратического отклонения S: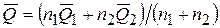 ;
; 
 ;
;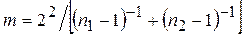 ;
; ;
; ;
; .
. .
.

 ,
,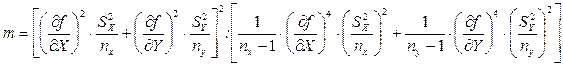 .
. .
. ;
; 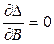 ;
;  ; … ;
; … ;  ,
,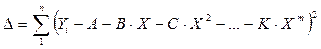 .
.
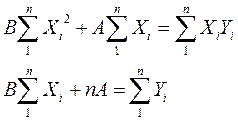

 .
.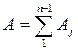 ,
,