Общие принципы проверки статистических гипотез

Полученные в экспериментах выборочные данные всегда ограничены и носят в значительной мере случайный характер. Именно поэтому для анализа таких данных и используется математическая статистика, позволяющая обобщать закономерности, полученные на выборке, и переносить их в реальные условия жизни.

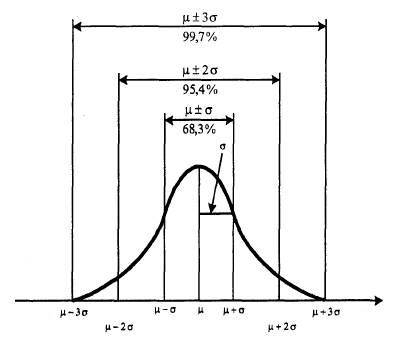
2.1 Понятие нормального распределения

Нормальное распределение играет большую роль в математической статистике, поскольку многие статистические методы предполагают, что, анализируемые с их помощью экспериментальные данные распределены нормально. График нормального распределения имеет вид колоколообразной кривой (рис. 1).

Рис.1. Кривая нормального распределения

Его важной особенностью является то, что форма и положение графика нормального распределения определяется только двумя параметрами: средним значением µ (мю) и стандартным отклонением σ (сигма).

«Нормальным» такое распределение было названо потому, что оно наиболее часто встречалось в естественнонаучных исследованиях и казалось «нормой» распределения случайных величин.

В реальных психологических экспериментах редко получаются данные, распределенные строго по нормальному закону. В большинстве случаев сырые психологические данные часто дают асимметричные, «ненормальные» распределения. По мнению Е.В.Сидоренко, причина этого заключается в самой специфике некоторых психологических признаков, когда от 10 до 20% испытуемых могут получить либо очень низкие, либо очень высокие оценки по методикам. Распределение таких оценок не может быть нормальным, как бы ни увеличивался объем выборки.

Важнейшими первичными статистиками, по которым проверяется нормальность распределения выборочных эмпирических данных, являются:

а) средняя арифметическая величина (среднее) - величина, сумма отрицательных и положительных отклонений выборочных данных от которой равна нулю. В статистике ее обозначают буквой М или Х;

б) мода – это числовое значение измеряемой характеристики, которое встречается в выборке наиболее часто. Мода обозначается как М_о;

в) медиана – это числовое значение измеряемой характеристики, по отношению к которой по крайней мере 50% выборочных значений меньше нее и по крайней мере 50% - больше. Обозначается как М_е;

г) cpеднее квадратичное отклонение (стандартное отклонение) - мера разнообразия входящих в группу объектов. Она показывает, на сколько в среднем отклоняется каждая варианта (конкретное значение оцениваемой характеристики) от средней арифметической величины. Обозначается греческой буквой s (сигма) Чем сильнее разбросаны варианты относительно средней арифметической величины, тем большим оказывается среднее квадратичное отклонение.

Cигма - величина именованная и зависит не только от степени варьирования, но и от единиц измерения. Поэтому по сигме можно сравнивать изменчивость лишь одних и тех же показателей, а сопоставлять сигмы разных признаков по абсолютной величине нельзя. Для того, чтобы сравнить по уровню изменчивости признаки любой размерности (выраженные в различных, единицах измерения) и избежать влияния масштаба измерении средней арифметической на величину сигмы, применяют коэффициент вариации, который представляет собой по существу приведение к одинаковому масштабу величины s.

д) коэффициент вариации - частное от деления сигмы на среднее, умноженное на 100%. Обозначается коэффициент вариации как CVи вычисляется по формуле:

CV= s/М*100%. (2.1)

Для нормального распределения эмпирических данных характерна закономерность, установленная между модой, медианой и средним и выражающаяся в следующем равенстве:

М=М_о=М_е.(2.2)

Для нормального распределения известны точные количественные зависимости частот и значений, позволяющие прогнозировать появление новых вариант:

· слева и справа от средней арифметической величины лежит 50% вариант;

· в интервале от М-1s до М+1s лежат 68,3% всех вариант;

· в интервале от М-2s до М+2s лежат 95,4% вариант;

· в интервале от М-3s до М+3s лежат 99,7% вариант [2].

Таким образом, ориентируясь на эти характеристики нормального распределения можно оценить степень близости к нему рассматриваемого распределения.

Следующими по важности являются такие первичные статистики как коэффициент асимметрии и эксцесс.

Коэффициент асимметрии (А) – численная мера скошенности распределения в левую или правьте сторону по оси ординат. Коэффициент ассиметрии вычисляется по формуле:

_N _

А= Σf_i(x_i-x)³/N*s³ (2.3)

ⁱ⁼¹

где f_i – частота x_i-го значения измеряемой характеристики в выборочных данных;

N – объем выборочных данных.

Если правая ветвь кривой распределения длиннее левой (правосторонняя скошенность) - говорят о положительной асимметрии, в противоположном случае (левосторонняя скошенность) - об отрицательной. Для нормального (симметричного) распределения коэффициент асимметрии равен нулю (А=0).

Эксцесс (Е) – количественная мера «горбатости» распределения, показатель островершинности (туповершинности) кривой распределения.

Коэффициент эксцесса вычисляется по формуле:

_N _

Е = Σf_i(x_i-x)⁴/N*s⁴-3 (2.4)

ⁱ⁼¹

Кривые, более высокие в своей средней части, островершинные, называются эксцессивными, у них большая величина эксцесса и его значение имеет положительный знак. При уменьшении величины эксцесса кривая становится все более плоской, приобретая вид плато, а затем и седловины - с прогибом в средней части. При этом значение эксцесса имеет отрицательный знак. Величина эксцесса в нормальном распределении равняется нулю (Е=0).

Эти параметры позволяют составить первое приближенное представление о характере распределения.

Точную и строгую оценку нормальности распределения можно получить, используя один из существующих методов проверки, например, с помощью критерия «хи-квадрат» Пирсона χ²_эмп [2]. Пример решения такой задачи будет рассмотрен в подразделе 3.1.

Начать с анализа первичных статистик надо еще и по той причине, что они весьма чувствительны к наличию выпадающих вариант. На практике же, очень большие эксцесс и асимметрия часто являются индикатором ошибок при подсчетах вручную или ошибок при введении данных через клавиатуру при компьютерной обработке. Грубые промахи при введении данных в обработку можно обнаружить, если сравнить величины сигм у аналогичных параметров. Выделяющаяся величиной сигма может указывать на ошибки.

Если обнаружены «подозрительные» значения, то необходимо принять обоснованное решение об их выбраковке. Его можно принять, используя достаточно мощный параметрический критерий t. Он рассчитывается по следующей формуле:

t = (V-M)/s ³t_st, (2.5)

где t - критерий выпада;

V - выпадающее значение признака;

М - средняя арифметическая величина признака для всей группы, включающей артефакт;

t_st - стандартные значения критерия выпадов, определяемые для трех уровней доверительной вероятности по таблице 1 (приложение 1).

Смысл критерия в том, чтобы определить, находится ли данная варианта в интервале, характерном для большинства членов выборки, или же - вне его.

Допустим, нами принят уровень значимости 0,05 (доверительная вероятность 0,95), а значение критерия составило 1,5. Поскольку 95% вариант лежат в пределах М±1.96s (1,5 меньше 1,96), следовательно, данная варианта лежит в указанном интервале. Если же значение критерия больше, например, 2,4, то это означает, что данное значение не относится к анализируемой совокупности (выборке), включающей 95% вариант, а есть проявление иных закономерностей, ошибок и пр. и должно быть, поэтому, исключено из рассмотрения.

Например, в эксперименте вы предлагаете решать мыслительные задачи и регистрируете в числе других параметров время решения. При просмотре данных обнаруживаете, что у одного из испытуемых время решения заметно больше, чем у остальных. Это бывает связано с тем, что вместо решения очередной задачи, испытуемый начинает «искать закономерность более широкого плана», «выводить общий принцип» или нечто подобное. Об этом он может сообщить экспериментатору, но может и не сообщать. Понятно, что время решения конкретной задачи при этом может сильно отличаться от средней величины. В этом случае вы окажетесь перед необходимостью принять обоснованное решение - включать данное значение в дальнейшую обработку или нет.

Предположим, в вашем эксперименте были получены следующие значения некоторого параметра: 10, 20, 20, 30, 30, 40, 40, 50, 210. В нашем примере n=9. Вычисляем: M=50; s=61. Можно ли считать значение 210 выпадающим?

210-50

t = -------------- = 2,62;

t_st (по табл.1) = 2,43 (для p>0,05)

Следовательно, значение 210 может считаться выпадающим и должно быть исключено из дальнейшей обработки.

После исключения выпадающих значений первичные статистические параметры вычисляются заново.

Существует правило, согласно которому все расчеты вручную должны выполняться дважды (особенно ответственные - трижды), причем желательно разными способами, с вариацией последовательности обращения к числовому массиву.

Оценка генеральной совокупности на основе выборочных данных недостаточно точна, имеет некоторую большую или меньшую ошибку. Такие ошибки, представляющие собой ошибки обобщения, экстраполяции, связанные с перенесением результатов, полученных при изучении выборки, на всю генеральную совокупность, называются ошибками репрезентативности.

Репрезентативность - степень соответствия выборочных показателей генеральным параметрам.

Статистические ошибки репрезентативности показывают, в каких пределах могут отклоняться от параметров генеральной совокупности (от математического ожидания или истинных значений) наши частные распределения, полученные на основании конкретных выборок. Очевидно, что величина ошибки тем больше, чем больше варьирование признака и чем меньше выборка. Это и отражено в формулах для вычисления статистических ошибок, характеризующих варьирование выборочных показателей вокруг их генеральных параметров.

В число первичных статистик входит статистическая ошибка средней арифметической величины. Формула для её вычисления такова:

m_M = ± s/n^1/2, (2.6)

где m_M - ошибка среднего;

s - стандартное отклонение;

n - число значений признака.

2.2. Понятие выборки

Выборка - любая группа испытуемых, выделенных из совокупности всех людей, относительно которых учёный намерен сделать выводы при изучении конкретной проблемы (генеральная совокупность) [2].

Выборки называются независимыми (несвязанными), если процедура эксперимента и полученные результаты измерения некоторого свойства у испытуемых одной выборки не оказывают влияния на особенности протекания этого же эксперимента и результаты измерения этого же свойства у испытуемых (респондентов) другой выборки.

И, напротив, выборки называется зависимыми (связанными), если процедура эксперимента и полученные результаты измерения некоторого свойства, проведенные на одной выборке, оказывают влияние на другую.

Следует подчеркнуть, что одна и та же группа испытуемых, на которой дважды проводилось психологическое обследование (пусть даже разных психологических качеств, признаков, особенностей), всё равно оказывается зависимой, или связной выборкой.

2.3. Проверка статистических гипотез

Полученные в экспериментах выборочные данные всегда ограничены и носят в значительной мере случайный характер. Именно поэтому для анализа таких данных и используется математическая статистика, позволяющая обобщать закономерности, полученные на выборке, и распространять их на всю генеральную совокупность.

В начале математической обработке данных экспериментатором выдвигается статистическая гипотеза - формальное предположение о том, что сходство (или различие) некоторых эмпирических данных случайно или, наоборот, неслучайно.

Сущность проверки статистической гипотезы заключается в том, чтобы установить, согласуются ли экспериментальные данные и выдвинутая гипотеза, допустимо ли отнести расхождение между гипотезой и результатом статистического анализа экспериментальных данных за счет случайных причин? Таким образом, статистическая гипотеза это научная гипотеза, допускающая статистическую проверку, а математическая статистика это научная дисциплина, задачей которой является научно обоснованная проверка статистических гипотез.

При проверке статистических гипотез используются два понятия: так называемая нулевая (обозначение Н₀) и альтернативная гипотеза (обозначение Н₁).

Принято считать, что нулевая гипотеза Н₀ - это гипотеза о сходстве, а альтернативная Н₁ - гипотеза о различии. Таким образом, принятие нулевой гипотезы Н₀ свидетельствует об отсутствии различий, а гипотезы Н₁ о наличии различий.

При проверке гипотезы экспериментальные данные могут противоречить гипотезе Н₀, тогда эта гипотеза отклоняется. В противном случае, т.е. если экспериментальные данные согласуются с гипотезой Н₀, она не отклоняется. Часто в таких случаях говорят, что гипотеза Н₀ принимается.

Отсюда видно, что статистическая проверка гипотез, основанная на экспериментальных данных, неизбежно связана с риском (вероятностью) принять ложное решение. При этом возможны ошибки двух родов. Ошибка первого рода произойдет, когда будет принято решение отклонить гипотезу Н₀, хотя в действительности она оказывается верной. Ошибка второго рода произойдет когда будет принято решение не отклонять гипотезу Н₀, хотя в действительности она будет неверна. Очевидно, что и правильные выводы могут быть приняты также в двух случаях. Вышесказанное представлено в таблице 1:

Таблица 1

Статистические ошибки

Не исключено, что исследователь может ошибиться в своем статистическом решении. Поскольку исключить ошибки при принятии статистических гипотез невозможно, то необходимо минимизировать возможные последствия, т.е. принятие неверной статистической гипотезы. В большинстве случаев единственный путь минимизации ошибок заключается в увеличении объема.

При обосновании статистического вывода следует решить вопрос, где же проходит линия между принятием и отвержением нулевой гипотезы? В силу наличия в эксперименте случайных влияний эта граница не может быть проведена абсолютно точно. Она базируется на понятии уровня значимости.

Уровнем значимости называется вероятность ошибочного отклонения нулевой гипотезы. Или, иными словами, уровень значимости это вероятность ошибки первого рода при принятии решения. Для обозначения этой вероятности, как правило, употребляют латинскую букву p.

Исторически сложилось так, что в прикладных науках, использующих статистику, и в частности в психологии, считается, что низшим уровнем статистической значимости является уровень р=0,05; достаточным - уровень р=0,01 и высшим уровень р=0,001.

Величины 0,05, 0,01 и 0,001 - это так называемые стандартные уровни статистической значимости. При статистическом анализе экспериментальных данных психолог в зависимости от задач и гипотез исследования должен выбрать необходимый уровень значимости. Как видим, здесь наибольшая величина, или нижняя граница уровня статистической значимости, равняется 0,05 - это означает, что допускается пять ошибок в выборке из ста элементов (испытуемых) или одна ошибка из двадцати элементов. Считается, что ни шесть, ни семь, ни большее количество раз из ста мы ошибиться не можем. Цена таких ошибок будет слишком велика.

2.4. Этапы принятия статистического решения

Принятие статистического решения разбивается на семь этапов [2].

1. Формулировка нулевой и альтернативной гипотез.

2. Определение объема выборки n. Для психологических исследований рекомендуется использовать экспериментальную и контрольную группы, так чтобы численность обоих сравниваемых групп была не менее 30-35 испытуемых в каждой. Планирование эксперимента должно включать в себя учет как объема выборки, так и ряда ее особенностей. Так, в психологических исследованиях важно соблюдение однородности выборки. Оно означает, что психолог, изучая, например, подростков, не может, включать в эту же выборку взрослых людей. Экспериментальная выборка должна представлять (моделировать) генеральную совокупность, поскольку выводы, полученные в эксперименте, предполагается в дальнейшем перенести на всю генеральную совокупность (репрезентативность).

3. Выбор соответствующего уровня значимости или вероятности отклонения нулевой гипотезы. Это может быть величина меньшая или равная 0,05. В зависимости от важности исследования можно выбрать уровень значимости в 0,01 или даже в 0,001. Как правило, если выборка испытуемых менее 100 человек, используется уровень значимости, равный 0,05.

4. Выбор статистического метода, который зависит от типа решаемой психологической задачи.

5. Вычисление соответствующего эмпирического значения по экспериментальным данным, согласно выбранному статистическому методу.

6. Определение статистической достоверности полученных значений, соответствующих выбранному вами уровню значимости (p=0,05, p=0,01, p=0,001).

7. Формулировка принятия решения (выбор соответствующей гипотезы Н₀ или Н₁).

2.5. Психологические задачи, решаемых с помощью статистических методов

Подавляющее большинство задач, решаемых психологом в эксперименте, предполагает те или иные сопоставления. Это могут быть сопоставления одних и тех же показателей в разных группах испытуемых или, напротив, разных показателей в одной и той же группе.

Для определения степени эффективности каких-либо воздействий (обучение, тренировка, тренинг, инструктаж и т.п.) сравниваются показатели «до» и «после» этих воздействий. Например, сравниваются показатели уровня тревожности у подростков до и после психотренинга, что позволяет определить его эффективность. Или в лонгитюдном исследовании сопоставляются результаты у одних и тех же испытуемых по одним и тем же методикам, но в разном возрасте, что позволяет выявить временную динамику анализируемых показателей.

Два выборочных распределения сравниваются между собой или с теоретическим законом распределения, чтобы выявить различия или, напротив, сходство в типах распределений. Например, сравнение распределений времени решения простой и сложных задач позволит построить классификацию задач и типологию испытуемых.

В целом, психологические задачи, решаемые с помощью методов математической статистики, условно можно разделить на несколько групп:

1. Задачи, требующие установления сходства или различия.

2. Задачи, требующие установления связи между данными.

3. Задачи, требующие группировки и классификации данных.

4. Задачи, требующие определения процентного соотношения изучаемого свойства.

Не нашли, что искали? Воспользуйтесь поиском по сайту: