
|
|
Понятие рациональной дроби.12 2.1.1. Определение. Рациональной дробью (или дробно-рациональнойфункцией) называется функция, равная отношению двух многочленов: ¦(x)= Рациональная дробь 2.1.2. Теорема. Всякую неправильную дробь
2.1.2. Правило: Для того, чтобы представить неправильную дробь 2.1.3. Упражнение. Представить в виде суммы многочлена и правильной дроби дробь: a) б) в) Решение. a) Разделим с остатком числитель 3x4-2x3+x2-x-1 на знаменатель x2-3: 3x4-2x3+x2-x-1=(x2-3)(3x2-2х+10)+(-7х+29) (см. 1.2.2 предыдущего параграфа). Поэтому Ответ: а) Простейшие рациональные дроби. 2.2.1. Определение. Правильные рациональные дроби вида Простейшие дроби принято разбивать на четыре вида:
2.2.2. Теорема. Всякую правильную рациональную дробь можно представить единственным образом в виде суммы простейших дробей:
+ + где А1, А2, …, B1, B2, …, C1, C2, …, D1, D2, …, M1, M2, …, N1, N2, …, - некоторые действительные числа. Например
+ Здесь действительные коэффициенты A, B, C, D, E, F, G, H требуют вычислений. 2.2.3. Если для дроби 1. Правую часть равенства (2.1.1) приведём к общему знаменателю Qn(x); в результате получим тождество 2. Так как в полученном равенстве (тождестве) знаменатели равны, то равны (тождественно) и числители, то есть равны многочлены, стоящие в числителях дробей равенства: Pm(x)=S(x). 3. Так как многочлены равны тогда и только тогда, когда равны соответствующие коэффициенты (см. 1.1.4), то, приравняв коэффициенты при одинаковых степенях в обеих частях равенства Pm(x)=S(x), получим систему линейных уравнений, из которой определяются искомые коэффициенты А1, А2, …, B1, B2, …, C1, C2, …, D1, D2, …, M1, M2, …, N1, N2, …,. 2.2.4. Упражнение. Представить дробь в виде суммы простейших: a) в) Решение. а) Имеем
= = То есть Так как в полученном равенстве (тождестве) знаменатели равны, то равны (тождественно) и числители, то есть равны многочлены, стоящие в числителях дробей равенства: х-1=(A+C)x2+(3A+B+4C)x+(2A+B+4C). Так как многочлены равны тогда и только тогда, когда равны соответствующие коэффициенты, то, приравняв коэффициенты при одинаковых степенях в обеих частях полученного равенства, получим систему линейных уравнений:
решая которую, например, методом Гаусса, определяем искомые коэффициенты А, В, С:
Û Таким образом, Ответ: 2.2.5. Теорема. Всякую рациональную дробь можно представить в виде суммы некоторого многочлена (возможно, нулевого) и простейших дробей. 2.2.6. Упражнение. Представить дробь в виде суммы многочлена и простейших дробей. a) б) в) Решение. a) Представим сначала дробь в виде суммы некоторого многочлена и правильной рациональной дроби: (см. решение упражнения 2.1.3 а))
=
Окончательно имеем
Ответ: а) + 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где Pm(x) - многочлен степени m, Qm(x) - многочлен степени п. При этом Pn(x) называется числителем дроби, а Qm(x) - её знаменателем.
, где Pm(x) - многочлен степени m, Qm(x) - многочлен степени п. При этом Pn(x) называется числителем дроби, а Qm(x) - её знаменателем.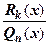 :
:
 ;
; .
. .
. , ,
, ,  , где p2-4q<0, k≥1, A, B, a, p, q - действительные числа, называются простейшими рациональными дробями.
, где p2-4q<0, k≥1, A, B, a, p, q - действительные числа, называются простейшими рациональными дробями. - простейшая дробь первого вида;
- простейшая дробь первого вида; - простейшая дробь третьего вида;
- простейшая дробь третьего вида;
 =
=  +
+  +…+
+…+  +
+  +
+  +…+
+…+  +…+
+…+ +
+ 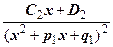 +…+
+…+ 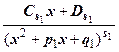 +…+ (2.1.1)
+…+ (2.1.1) +
+  +…+
+…+  .
. =
=  +
+  +
+  ,
, =
=  +
+  +
+  +
+  ,
, =
=  +
+  +
+ +
+  +
+ 
 на неприводимые множители, то можно выписать её представление в виде (2.1.1). Для нахождения неопределённых коэффициентов А1, А2, …, B1, B2, …, C1, C2, …, D1, D2, …, M1, M2, …, N1, N2, …, в этом равенстве можно применить, например, метод неопределённых коэффициентов, который заключается в следующем:
на неприводимые множители, то можно выписать её представление в виде (2.1.1). Для нахождения неопределённых коэффициентов А1, А2, …, B1, B2, …, C1, C2, …, D1, D2, …, M1, M2, …, N1, N2, …, в этом равенстве можно применить, например, метод неопределённых коэффициентов, который заключается в следующем: , где S(x) - многочлен неопределёнными коэффициентами А1, А2, …, B1, B2, …, C1, C2, …, D1, D2, …, M1, M2, …, N1, N2, ….
, где S(x) - многочлен неопределёнными коэффициентами А1, А2, …, B1, B2, …, C1, C2, …, D1, D2, …, M1, M2, …, N1, N2, …. ;
; =
= =
= ,
,
 Û
Û  Û
Û  Û
Û 
 +
+  -
-  .
. =
=  +
+  =
=  =
= ;
; Û
Û  Û
Û 
 =
=  -
-  .
.