
|
|
Радиальное уравнение. Главное и орбитальное квантовые числа.Основы квантовой физики атомов.
Водородоподобные атомы. Уравнение Шредингера для электрона в водородоподобном атоме.
Водородоподобные атомы представляют собой системы, состоящие из ядра, заряд которого
Рассмотрим систему, состоящую из ядра и электрона. Потенциальная энергия взаимодействия ядра и электрона равна
Движение двух частиц осуществляется вокруг общего центра масс, тогда ( кинетические энергии Отношение энергий ядра и электрона для атома водорода
В приближении прямоугольной потенциальной ямы минимальная энергия обратно пропорциональна массе частицы
Поэтому ядро можно считать неподвижной частицей, создающей потенциальную яму для электрона. Потенциальная энергия электрона в атоме водорода Уравнение Шредингера для стационарных состояний электрона в водородоподобном атоме с учетом вида
где или
Оператор Лапласа в сферических координатах имеет вид:
Уравнение Шредингера в сферических координатах для электрона в водородоподобном атоме
Движения по координатам
Полную энергию электрона можно представить в виде:
Уравнение Шредингера примет вид
Разделим это выражение почленно на
Это уравнение содержит слагаемые, зависящие от - радиальная часть
или после преобразований
- угловая часть
или
- это оператор Лежандра,
Применим оператор
т.к. Тогда можно записать
Собственные значения энергии
Таким образом, уравнение Шредингера можно представить в виде системы из двух уравнений, радиального и углового:
Радиальное уравнение. Главное и орбитальное квантовые числа.
Мы получили радиальное уравнение:
или
т.к. где Радиальная функция
где
- полином Лагерра, имеющий ( Из свойств полиномов Лагерра следует, что решение В системе координат, вращающейся с электроном потенциальная энергия электрона будет:
Второе слагаемое этого выражения –потенциальная энергия в поле центробежных сил. Если энергия электрона Если По теории Бора
Эти результаты подтверждаются опытом, и для квазиклассического случая (при больших n) является справедливым
Тогда по Бору
где
Откуда При Суть проблемы: в квантовой яме микрообъект не может покоиться. Основное состояние электрона в атоме водорода: Это состояние сферически симметрично, т.е. зависит только от
Решением этого уравнения будет функция вида:
Находим
Подставляя эти выражения в радиальное уравнение, получим:
или
Для того, чтобы это равенство выполнялось при любых при при Тогда Строгое решение уравнения Шредингера для основного состояния электрона в атоме согласуется с выводами теории Бора. С теорией Бора не совпадает следующее: орбитальное движение электрона полностью отсутствует, но радиус Бора, как параметр волновой функции есть. Волновая функция для электрона в основном состоянии в атоме водорода:
Вероятность локализации электрона в некотором объеме
Вследствие сферической симметрии, распределение плотности вероятности зависит от модуля радиуса
Тогда
Значение 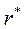 можно найти из условия можно найти из условия  , т.е. , т.е.
Откуда Первая боровская орбита соответствует области, где плотность вероятности локализации электрона в зависимости от модуля радиуса максимальна. Тогда
Из условия нормировки:
следует, что
Для водородоподобного атома При При

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и одного электрона (заряд
и одного электрона (заряд  ). Примеры: Н, D, T, He+, Li++ и т.д.
). Примеры: Н, D, T, He+, Li++ и т.д.
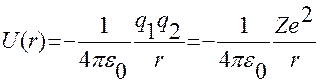 .
. ),
), и
и  .
. .
. .
.
 ,
, - полная энергия электрона;
- полная энергия электрона; ,
,
 - оператор Лапласа:
- оператор Лапласа:
 .
. .
.
 в сферически симметричном поле являются независимыми, и функцию
в сферически симметричном поле являются независимыми, и функцию  можно представить в виде произведения трех функций, каждая из которых зависит лишь от одной переменной:
можно представить в виде произведения трех функций, каждая из которых зависит лишь от одной переменной: или
или  ,
, - радиальная функция, описывающая радиальное движение электрона,
- радиальная функция, описывающая радиальное движение электрона, - угловая функция, описывающая вращение электрона относительно ядра в водородоподобном атоме (ротатор).
- угловая функция, описывающая вращение электрона относительно ядра в водородоподобном атоме (ротатор).

 , получим:
, получим:
 ,
,  и
и  . Вследствие независимости движений по координатам
. Вследствие независимости движений по координатам  , это уравнение должно выполняться при любых значениях
, это уравнение должно выполняться при любых значениях  и при их независимом изменении. Оно распадается на части, зависящие от
и при их независимом изменении. Оно распадается на части, зависящие от  и от
и от  :
:
 ;
;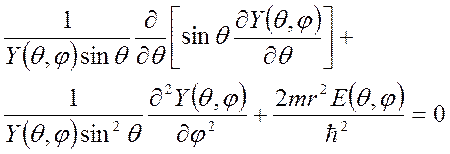
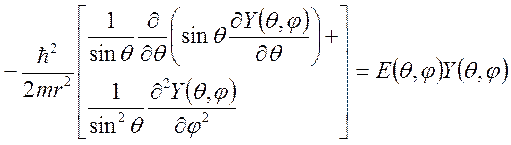

 - оператор момента импульса, поэтому угловое уравнение можно записать в виде
- оператор момента импульса, поэтому угловое уравнение можно записать в виде .
.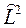 к
к  :
: ,
, и
и  , где
, где  - орбитальное квантовое число.
- орбитальное квантовое число. .
. .
.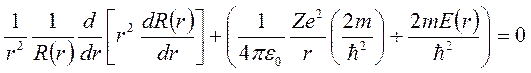 .
.
 ;
;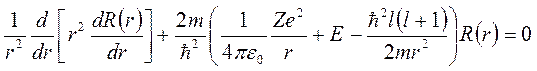 ,
, ,
, - полная энергия электрона.
- полная энергия электрона. имеет вид:
имеет вид: ,
, .
.
 ) корней,
) корней, 
 существует только при
существует только при  .
. .
. , то его движение инфинитно.
, то его движение инфинитно.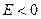 , то электрон находится в потенциальной яме (его движение финитно).
, то электрон находится в потенциальной яме (его движение финитно).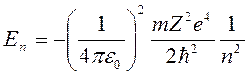 и
и 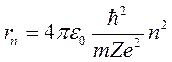 .
. .
. ,
, ,
, .
. , следовательно,
, следовательно,  .
.
 , при
, при 
 . Отсюда следует, что
. Отсюда следует, что  .
. ,
,  ,
,  .
. необходимо решить радиальное уравнение:
необходимо решить радиальное уравнение: ,
, .
.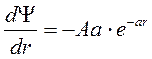 ;
;  .
.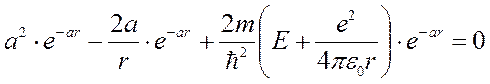 ,
, .
. , коэффициенты при одинаковых степенях
, коэффициенты при одинаковых степенях 
 , откуда
, откуда  ;
;
 , откуда
, откуда  .
. .
. .
.
 .
. , независимо от его направления. Поэтому элемент объема
, независимо от его направления. Поэтому элемент объема 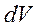 целесообразно выбрать в виде сферического слоя между радиусами
целесообразно выбрать в виде сферического слоя между радиусами  :
: .
. 
 , где
, где  .
.
 имеет максимум при
имеет максимум при 

 .
. . - это радиус первой боровской орбиты.
. - это радиус первой боровской орбиты.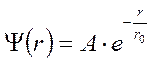 .
.
 . И волновая функция имеет вид:
. И волновая функция имеет вид:
 .
. .
. - электрон принимает любые значения кинетической энергии – он свободе.
- электрон принимает любые значения кинетической энергии – он свободе. полная энергия электрона в водородоподобном атоме
полная энергия электрона в водородоподобном атоме .
. - главное квантовое число, оно определяет энергию электрона в атоме.
- главное квантовое число, оно определяет энергию электрона в атоме.