
|
|
Поиск оптимума целевой функции методом крутого восхождения (градиентный метод, или метод Бокса-Уилсона)12 Планирование эксперимента начинают с дисперсионного анализа, чтобы установить, оказывает ли существенное влияние некоторый качественный или количественный фактор Например, если требуется выяснить, влияет ли количество организационно – распорядительных документов на число возникающих нештатных ситуаций в процессе принятия управленческих решений. Основная идея дисперсионного анализа состоит в сравнении «факторной дисперсии», порождаемой воздействием фактора, то есть дисперсии влияния и «остаточной дисперсии», обусловленной случайными причинами, то есть дисперсии воспроизводимости опытов. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на Если уже установлено, что фактор существенно влияет на Схема применения дисперсионного анализа следующая. Сначала проводят эксперимент с объектом управления согласно таблице 1. Таблица 1 – Форма бланка планируемого эксперимента
Здесь Дисперсия влияния x на
Дисперсию воспроизводимости опытов оценивают выражением
Расхождение между Если окажется, что Регрессионный анализ Следующим этапом является регрессионный анализ, который позволяет получить математическое описание исследуемого процесса, т.е. получить уравнение регрессии, выражающее зависимость среднего значения выходного параметра от уровней значений факторов. Например, если мы занимаемся исследованием влияния стажа работы, квалификации и возраста одновременно на производительность труда, то уравнение регрессии должно получиться в виде: y = b0 + b1x1+ b2x2+ b3x3, где x1 – стаж работы; x2 – возраст; x3 – квалификация; b0 – свободный член уравнения; b1; b2; b3 – коэффициенты при факторах. Таким образом, если мы определим значение этих коэффициентов, то можно прогнозировать величину производительности труда при различных значениях факторов. Задача состоит в том, чтобы подобрать такое сочетание факторов, чтобы получить оптимальное значение y. Уравнение регрессии ищут в результате проведения полного факторного эксперимента (ПФЭ) на основе матрицы планирования эксперимента. ПФЭназывают эксперимент, в котором реализуются все возможные сочетания уровней факторов. Если число факторов n , а каждый фактор может принимать два значения: верхнее и нижнее, то число всех опытов в ПФЭ N = 2n. Может иметь место корреляция факторов, в этом случае уравнение регрессии дополняют коэффициентами взаимодействия факторов bij . Эффект взаимодействия проявляется в том случае, если влияние одного фактора зависит от того, на каком уровне находится другой факторj. При построении матрицы планирования ПФЭ пользуются следующими правилами: v первая строка выбирается так, чтобы управляемые факторы xi находились либо на верхнем, либо на нижнем уровне. v смена знака в первом столбце (фактор x1) осуществляется для каждого нового опыта, а частота смены знака для каждого последующего фактора вдвое меньше, чем для предыдущего. Например, для ПФЭ типа 23 матрица планирования эксперимента выглядит следующим образом
Таблица 1
До сих пор мы рассматривали полный факторный эксперимент без учета взаимодействия факторов. В ряде практических задач влияние этих взаимодействий оказывается настолько велико, что не учет последних может привести к грубым ошибкам, поэтому матрица планирования должна учитывать эти взаимодействия. Составим матрицу планирования с учетом взаимодействия для трех факторов
В каждой точке факторного пространства проводится m – опытов, т.е. каждый опыт дублируют m раз. Обычно m = 2;3. Тогда среднее арифметическое значение каждого опыта будет вычисляться по формуле
Опыты второй серии выполняют только после того, как закончены опыты первой серии и т.д., последовательность постановки опытов внутри каждой из m серий выбирают случайным образом . Делается это для того, чтобы исключить влияние систематических ошибок, вызванных внешними условиями.
Далее проверяют воспроизводимость опытов Опыты считают воспроизводимыми, если их дисперсии Si 2(y) однородны. Дисперсия каждого опыта рассчитывается по формуле
Si 2(y) =
Дисперсии считаются однородными, если отношение дисперсии Si 2(y) в той точке факторного пространства, глее она максимальна, к сумме всех дисперсий опытов, меньше критического значения критерия Кочрена Gmax = Сравниваем значение критерия с табличным значением G(α;f1; f2 ), где число степеней свободы f1 = m-1; f2 = N. если Gmax< G(α;f1;f2), H0 – принимается, т.е. дисперсии однородны и опыты воспроизводятся. если Gmax> G(α;f1;f2), H0 – отвергается, т.е. дисперсии неоднородны, опыты не воспроизводятся. Причиной невоспроизводимости опытов может явиться неучёт какого либо влияющего фактора, либо велика погрешность опытов. После оценки воспроизводимости опытов переходят к вычислению коэффициентов модели, т.е. коэффициентов уравнения регрессии в виде полинома первой степени, т.е. уравнение регрессии для трёх факторов: y = b0 + b1x1+ b2x2+ b3x3+ b12x1x2+ b13x1x3 + b23x2x3 + b123 x1x2x3, b0 – свободный член уравнения, b0 = bi = где i – номер фактора, для которого вычисляется коэффициент bi j – номер опыта; zij – знаковая функция, т.е. это знак ячейки ij. Модуль коэффициента выражает силу влияния фактора, а знак определяет направление влияния, то есть прямую или обратную зависимость. Смешанные коэффициенты: bij = ij – номера факторов; ziu; zju – знаковые функции. Если опыты не воспроизводятся по критерию Кочрена, то процедуру поиска следует приостановить, так как процесс не управляем. Смешанные коэффициенты выражают эффекты взаимодействия факторов, т.е. наличие корреляции между этими факторами. В этом случае влияние i-того фактора на y зависит от того, на каком уровне находится другой фактор, с которым коррелирует данный фактор. Если корреляции нет, то смешанные коэффициенты равны нулю. После того, как все коэффициенты определены, т.е. модель становиться известной, проверяют значимость коэффициентов модели с помощью критерия Стьюдента.Для этого вычисляют среднюю дисперсию S2(y) = Где Si2(y) – дисперсия i-того опыта в матрице планирования. Вычисляем дисперсию S2(bi) = где N –число опытов в матрице планирования, m- число повторных опытов. Вычисляем t – критерий tj = где S(bj) = Сравниваем полученный критерий с табличным значением. tα;f – критическое (табличное) значение критерия Стьюдента . Если tα;N(m-1) < tj , то H0 – принимается, коэффициенты значимы. Значимость коэффициентов проверяется для линейных членов уравнения. Причина не значимости коэффициентов уравнения регрессии может быть следующая -велика ошибка эксперимента, -мал интервал варьирования по данному фактору, -значение данного фактора в эксперименте близко к оптимальному. Завершается процесс статистической обработки результатов эксперимента проверкой адекватности модели. Адекватность модели оценивается с помощью критерия Фишера; F = S2ад. =
Сравниваем полученное значение критерия Фишера с табличным значением со степенями свободы f1 = N - Если F>F(α; ;f1;f2 ), то H0 – отвергается, то есть модель не адекватна. Чтобы получить адекватную модель при вычислении теоретических значений Для этого фактор xj для которого |bj| = max выбирают в качестве базового. Для него выбирают шаг движения по градиенту λj. Обычно величина шага составляет 1-2 интервала варьирования yj. Шаги по остальным факторам рассчитывают по формуле λi = Таким образом становятся известными шаги движения по градиенту для всех факторов. Далее планируем опыты в направлении градиента. Если мы движемся к максимуму, то реальное значение xi – фактора в первом опыте xi(1) = xiо+ Sign (bi)* λi ; i=1…n xi(2) = xiо+ 2Sign (bi)* λi - реальные значения факторов для второго опыта и так далее. В направлении градиента ставится не более 5-10 опытов, то есть xi (5) = xiо+ 5Sign (bi)* λi ; i=1…n. Количество шагов в направлении градиента ограничено, потому что при этом движении мы выходим из области адекватности модели. Если мы движемся к минимуму, то xi(1) = xiо - Sign (bi)* λi ; xi(k) = xiо - kSign (bi)* λi ; Знаковая функция Sign (bi) = -1,если bi < 0; Sign(bi) = +1, если bi > 0. После проведения всех опытов по матрице планирования и в направлении градиента анализируют полученные результаты. Если наилучший опыт не удовлетворяет, то его выбирают за центр нового плана и процедуру оптимизации повторяют до тех пор, пока не достигнут цели.
Статистическая оптимизация производительности труда работников службы ДОУ Цель: определение идеального среднего статистического работника, обеспечивающего максимальную производительность труда. В качестве оценки производительности труда может выступать коэффициент использования рабочего времени ( отношение суммарного нормативного времени выполнения сотрудником различных видов работ в течение рабочего дня к его продолжительности ). В результате проведения дисперсионного анализа установлено, что основными влияющими факторами являются стаж работы по специальности, возраст и квалификация (разряд по тарифной сетке -всего 17 разрядов). Выбирают центр плана, то есть опорные, или основные (базовые) значения влияющих факторов, например стаж работы 20 лет, возраст 40 лет, квалификация 10 разряд. Назначают шаг (интервал) варьирования для каждого фактора, например для стажа работы 2 года, для возраста 3 года, для квалификации 1 разряд. Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называют ПФЭ. Если число факторов равно n и каждый из них варьируется на 2 уровнях, то число опытов N в ПФЭ составляет N = 2n. В этом случае говорят, что имеет место ПФЭ типа 2ⁿ. Составляют матрицу планирования полного факторного эксперимента, при этом число всех различных опытов для нашего примера равно 8 , т.к. n= 3. Значения факторов могут располагаться только на двух уровнях- верхнем и нижнем, которые отстоят от основного уровня на величину шага варьирования. Поэтому вводят понятие кодированного значения фактора, то есть безразмерную величину Для упрощения записи условий эксперимента и удобства последующего анализа полученных результатов масштабы факторов выбираются так, чтобы нижнему уровню соответствовало -1, верхнему +1, основному уровню - 0. Для количественных факторов это достигается с помощью следующего преобразования:
Xj0 - натуральное значение основного уровня,
Следовательно, верхнему уровню фактора будет соответствовать кодированное значение +1, а нижнему -1. При построении матрицы ПФЭ пользуются следующим правилом: первая строка назначается так, чтобы факторы принимали значения +1, либо все -1. Смена знака в первом столбце ( первый фактор) осуществляется для каждого нового эксперимента, смена знака для каждого последующего столбца (фактора) проводится в два раза реже, чем для предыдущего. Кроме того, каждый эксперимент дублируют m раз для повышения достоверности результатов и оценки воспроизводимости опытов (экспериментов). Итак, матрица ПФЭ является планом проведения эксперимента, то есть в соответствии с условиями проведения каждого опыта получают значения выходного параметра ( производительность труда) Y, которые заносят в соответствующие ячейки матрицы. Пример матрицы ПФЭ дан в таблице
Эта таблица (матрица) является основой для получения математической модели в виде полинома первой степени, связывающей параметр оптимизации и влияющие факторы. Модель в виде полинома первой степени используют для того, что для её получения требуется меньшее количество опытов, с другой стороны , как известно, в определённой локальной области факторного пространства любую нелинейную зависимость можно аппроксимировать линейной, то есть любую кривую линию можно представить отрезком прямой с определённой погрешностью. Для улучшения терминологии приведем в общем виде в качестве примера запись двух наиболее простых математических моделей, используемых в ПФЭ. 1) Для двух факторов У = Во + В1Х1 + В 2Х2 + В 12Х1Х2 2) для трех факторов У = Во + В1Х1 + В2Х2 + В3Х3 + В 12Х1Х2 + В 13Х 1Х 3 + В 23Х 2Х 3 + + В 123Х 1Х 2Х 3 Во - свободный член уравнения регрессии, равный среднеарифметическому значению параметра оптимизации У. В1Х1 , В 2Х2 , В 3Х 3 - линейные члены уравнения регрессии. В12Х1Х2 , В13Х 1Х 3 ,В23Х 2Х 3 , В123Х 1Х 2Х 3 - нелинейные взаимодействия факторов. Эффект взаимодействия (корреляция) проявляется в том случае, когда влияние одного фактора зависит от того, на каком уровне находится другой, или другие факторы. Вi - коэффициенты при независимых переменных Хi. Они указывают на силу влияния факторов на целевую функцию У. Чем больше по абсолютной величине Вi, тем больше его влияние на У. Если Вi - положительная величина, то при увеличении Хi У увеличивается, если коэффициент Вi отрицательный, то при возрастании Xi У - убывает. Таким образом, величина Вi соответствует вкладу Хi в величину У. Статистическую обработку результатов эксперимента (матрицы) проводят в следующем порядке. Сначала проверяют воспроизводимость результатов повторных опытов с помощью критерия Кочрена. Опыты считаются воспроизводимыми, если дисперсии Si²(У) целевой функции каждой точки факторного пространства однородны
среднеарифметическое значение в каждом опыте
Дисперсии считаются однородными, если отношение дисперсии У в той точке факторного пространства, где она максимальна к сумме дисперсий во всех точках, в которых проводился эксперимент, меньше критического
если Gmax < Gкр, то опыты воспроизводятся, Gкр выбирают из статистических таблиц для соответствующего уровня значимости, число степеней свободы при этом f1 = m – 1, f2= N. Если опыты не воспроизводятся, то процесс не управляем, не все факторы учтены или большая ошибка эксперимента. Надо добиваться того, чтобы опыты были воспроизводимы. Следующим шагом является вычисление коэффициентов уравнения регрессии, то есть коэффициентов полинома первой степени по формулам y = b0 + b1x1+ b2x2+ b3x3+ b12x1x2+ b13x1x3 + b23x2x3 + b123 x1x2x3, где b0 – свободный член уравнения, b0 = bi = где i – номер фактора, для которого вычисляется коэффициент bi , j – номер опыта; zij – знаковая функция, т.е. это знак ячейки ij. Модуль коэффициента выражает силу влияния фактора, а знак определяет направление влияния, то есть прямую или обратную зависимость. Смешанные коэффициенты bij = где ij – номер смешанного фактора; ziu; zju – знаковые функции, то есть значения i и j безразмерного фактора в u-ом опыте. После вычисления коэффициентов оценивают их значимость с помощью критерия Стъюдента. Для этого вычисляют среднюю дисперсию S2(y) = где Si2(y) – дисперсия i-того опыта в матрице планирования. Вычисляем дисперсию S2(bi) = где N –число опытов в матрице планирования, m- число повторных опытов. Вычисляем t – критерий tj = где S(bj) = Сравниваем полученный критерий с табличным значением. tα;f – критическое (табличное) значение критерия Стьюдента . Если tα;N(m-1) < tj , то H0 – принимается, коэффициенты значимы. Значимость коэффициентов проверяется для линейных членов уравнения. Причины не значимости: уровень опорной точки близок к экстремуму, велика дисперсия опытов, то есть ошибка экспериментов, мал шаг варьирования. Далее оцениваем адекватность полученной модели по критерию Фишера F = S2ад. = где
Сравниваем полученное значение критерия Фишера с табличным значением со степенями свободы f1 = N - Если F>F(α; ;f1;f2 ), то гипотеза H0 – отвергается, то есть модель не адекватна и наоборот. Далее планируют движение по градиенту. Для наиболее влияющего фактора j выбирают шаг движения λj в направлении градиента, обычно шаг равен интервалу варьирования. Шаги по остальным факторам определяют
λi = Условия проведения опытов в направлении градиента выглядят: так как мы движемся к максимуму, то реальное значение xi – фактора в первом опыте xi(1) = xiо+ Sign (bi)* λi ; i=1,2,3; во втором опыте xi(2) = xiо+ 2Sign (bi)* λi и так далее. Число шагов в направлении градиента 5-10, так как при движении мы выходим из области определения модели ( из области её адекватности). Сравниваем все опыты и выбираем наилучший, если он не удовлетворяет, то его принимаем за центр нового плана и процедуру повторяем.
ВЫБОРОЧНЫЙ МЕТОД ПРИ ПРОВЕДЕНИИ АУДИТА ДОКУМЕНТОВ
Применение выборочного метода в аудите, как и в других сферах человеческой деятельности, заключается в замене сплошного наблюдения какой-либо генеральной совокупности объектов изучением некоторой ее части с последующим распространением результатов изучения на всю совокупность объектов. Обычно смысл применения выборочного метода в различных сферах заключается в небольшой "жертве качества" (сплошное наблюдение дает более достоверные результаты), обеспечивающей огромный выигрыш в затратах ресурсов - времени специалистов и т.п., поскольку, как правило, выборка по объему во много раз меньше генеральной совокупности. Выборочный метод является хорошо разработанной и многократно опробованной в различных приложениях конструкцией теории вероятностей. В качестве примера выборки приведем исследование правильности оформления документов определенного рода (наличие всех необходимых реквизитов, разрешительных подписей и т.п.), когда вместо всей совокупности таких документов рассматривается лишь часть из них. Здесь реализуется известная в теории вероятностей схема оценки вероятности определенного события - неправильность оформления документов - по его частоте в некоторой выборке из генеральной совокупности всех документов определенного рода. В рамках этой генеральной совокупности мы имеем дело с типичной задачей теории вероятностей - оценка математического ожидания генеральной совокупности по выборке из нее. Среднее арифметическое выборки из некоторой генеральной совокупности является обычно наилучшей оценкой математического ожидания этой совокупности. Однако это точечная оценка. В приложениях теории вероятности (точнее, ее раздела, называемого математической статистикой и занимающегося методами оценки вероятностных характеристик на базе экспериментальных данных) обычно стараются идти дальше и пользоваться кроме точечных еще и интервальными оценками. В качестве последних чаще всего используется так называемый доверительный интервал для математического ожидания генеральной совокупности. Это такой интервал, который с заданной - доверительной вероятностью бета (например, 0,95) накрывает неизвестное нам математическое ожидание. При доверительной вероятности бета, границы доверительного интервала для математического ожидания при естественных допущениях вычисляются по формуле
I = (Р - эпсилон, Р + эпсилон), (1)
1 n где Р = - SUM Xi, (2) n i=1
__ t эпсилон = / D ----- , (3) \/ __ /n \/
1 n 2 D = ----- SUM (Xi - Р) . (4) n – 1 i=1
Здесь Р – среднее арифметическое значение, полученное по выборке, то есть относительное количество неправильно оформленных документов; n - объем выборки; Xi –признак, характеризующий правильность оформления i-го документа выборки (признак равен 1, если документ неправильно оформлен, и признак равен 0, если документ оформлен правильно); t – критерий Стъюдента, зависящий от бета, значения которого имеются в таблицах справочников по математике (например, при бета = 0,95, t = 1,96). Вероятностная конструкция доверительного интервала хорошо сочетается с аудиторской конструкцией уровня существенности, то есть допустимой долей неправильно оформленных документов. Ведь смысл доверительного интервала при достаточно больших доверительных вероятностях (бета = 0,99, бета = 0,95 и т.п.) означает, что доверительный интервал практически всегда накрывает интересующий нас показатель, то есть среднее арифметическое значение доли неправильно оформленных документов в генеральной совокупности. Задача обычно ставится так. Есть генеральная совокупность из N элементов (например, документов определенного вида), по отношению к каждому из которых событие А (например, неправильное оформление) может иметь место, но может и отсутствовать. Обозначим через Р относительную частоту наступления события в выборке, то есть вероятность неправильного оформления документов. Для оценки степени распространенности события А в генеральной совокупности и уменьшения затрат труда делается выборка из n документов (обычно n гораздо меньше, чем N), подсчитывается число документов выборки, для которых событие А имеет место, и определяется отношение этого числа к n, то есть находим Р. Далее по величине Р необходимо сделать вывод о том, насколько распространено событие А во всей генеральной совокупности. Таким образом, перед нами - типичная для математической статистики задача оценки вероятности наступления некоторого события в генеральной совокупности по его относительной частоте в выборке. Иногда говорят об оценке генеральной доли, т.е. доли события А в генеральной совокупности, по выборочной доле. Обозначим порог существенности, то есть допустимую долю неправильно оформленных документов Р0, а нижнюю и верхнюю границы доверительного интервала соответственно Р1 и Р2. Здесь возможны три случая. В первом из них и Р1, и Р2 меньше порога существенности (например, Р1 = 5%, Р2 = 8%, а Р0 =10%), ввиду чего аудитор решает, что нарушения в оформлении всей совокупности документов данного вида несущественны. Во втором случае и Р1, и Р2 больше порога существенности, что позволяет сделать вывод о существенно неверной работе с документами данного вида и ставить вопрос о причинах неправильного их оформления. Наконец, самым сложным для принятия решения аудитором оказывается третий случай, когда Р1 меньше, а Р2 больше порога существенности. В этом случае полагаем эпсилон = Р – Р0 по модулю и по формуле (3) вычисляем новый объём выборки n. Заметим, что путь увеличения n сравнительно легко реализуем, так как отобрать ещё несколько документов, или десятков документов значительно просто. После исследования выборки увеличенного объёма ситуация прояснится, то есть результаты проверки правильности оформления документов будут либо положительными, либо отрицательными. Рассмотрим теперь частный, но важный в аудите случай, когда Р = 0. Например, аудитор случайным образом отобрал n документов и все они оказались оформленными правильно. Здесь возникает вопрос, остановиться или увеличить выборку. Тот же вопрос может иметь другую формулировку, нацеленную на планирование аудиторской проверки: какое число документов отбирать, с тем чтобы в случае правильного оформления их всех дальнейший отбор не производить. Согласно соотношениям (1 - 4) при отсутствии ошибок в выборке из n документов, т.е. при всех Хi = 0, а также Р = D = эпсилон = 0, доверительный интервал стягивается в точку. Этот случай рассматривается в общем виде в теории вероятностей и доведен там до достаточно простых расчетных соотношений. Например, n может определяться по формуле
n = lg (1 - бета) : lg (1 – P0) (5)
В формуле (5) lg - обозначение десятичного логарифма, а Р0 - порог существенности. В таблице 1 представлены для удобства предельные значения n объемов выборок в случае отсутствия отрицательных результатов при различных доверительных вероятностях бета и порогах существенности Р0, вычисленных по формуле (5).
Таблица 1
Приведенные в таблице 1 значения n удобно использовать при планировании аудита как начальные величины размера выборки на первом этапе. Например, если выбраны порог существенности Р0 = 0,1 и доверительная вероятность бета = 0,95, то согласно таблице целесообразно запланировать объем выборки n = 28 элементов. Если после обработки выборки окажется, что событие А ни разу не зафиксировано (все документы оформлены правильно), то работа по данной генеральной совокупности заканчивается с положительным итогом проверки. Если же хотя бы один раз событие А в выборке имело место, то необходимо переходить к ранее описанной общей процедуре. Обработку данных легко осуществить с помощью приложения Microsoft excell, используя статистический пакет. Таким образом, используя данный метод можно оценить качество подготовленных документов.
СТАТИСТИЧЕСКИЙ МЕТОД НОРМИРОВАНИЯ ТРУДА РАБОТНИКОВ СЛУЖБЫ ДОУ
Основой более рационального использования времени и преодоления его потерь является нормирование, то есть определение норм и нормативов его расходования. Под нормой временипонимается его регламентируемая величина, необходимая для производства единицы продукции, ее партии, или выполнения той или иной работы одним или группой исполнителей соответствующей квалификации в определенных организационно-технических и природно-климатических условиях. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
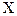 , который имеет
, который имеет 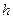 уровней
уровней  , на изучаемую величину
, на изучаемую величину 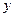 .
.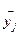
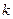
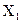
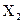 .
.
.
.
.
.
.
.


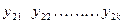 .
.
.
.
.
.
.
.
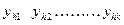
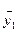
 .
.
..
.
.
..
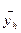
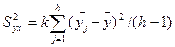
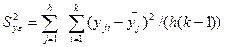
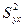 и
и 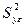 оценивают с помощью
оценивают с помощью 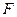 - критерия Фишера по формуле
- критерия Фишера по формуле 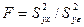 и сравнивают его с табличным критическим значением
и сравнивают его с табличным критическим значением 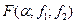 где
где  , то есть число степеней свободы,
, то есть число степеней свободы, 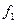 - это число степеней свободы для числителя (большей дисперсии),
- это число степеней свободы для числителя (большей дисперсии),  - число степеней свободы знаменателя (дисперсии воспроизводимости).
- число степеней свободы знаменателя (дисперсии воспроизводимости).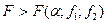 , то изучаемый фактор оказывает влияние на выходной параметр
, то изучаемый фактор оказывает влияние на выходной параметр  .
.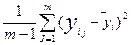
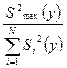 ;
;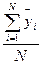 ;
;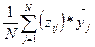 ,
,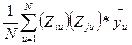 , т.е. перемножаются знаки столбцов.
, т.е. перемножаются знаки столбцов. ,
,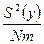 ,
,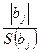 ,
,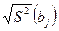 .
.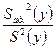 ;
; ;где
;где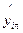 - значение выходного параметра, рассчитанное по уравнению регрессии, т.е. теоретическое значение;
- значение выходного параметра, рассчитанное по уравнению регрессии, т.е. теоретическое значение; - практическое значение выходного параметра из матрицы планирования;
- практическое значение выходного параметра из матрицы планирования;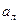 - число линейных членов уравнения, то есть число влияющих факторов.
- число линейных членов уравнения, то есть число влияющих факторов. λj
λj 
 .
. ,т.е. осуществляют переход к кодированному значению фактора,
,т.е. осуществляют переход к кодированному значению фактора,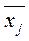 - натуральное значение фактора,
- натуральное значение фактора,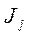 - интервал варьирования для j - фактора.
- интервал варьирования для j - фактора. ,
,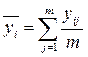
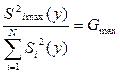 -критерий Кочрена,
-критерий Кочрена,