
|
|
Тема 2. Расчет тепловых эффектов химических реакций при различных температурахПРЕДИСЛОВИЕ Данное методическое руководство представляет собой пособие для практических занятий по дисциплине «Физическая химия», предназначенное для студентов технологических специальностей. Пособие ставит перед собою цель познакомить студентов с методами и приемами расчетов по основным разделам физической химии: «Основы химической термодинамики», «Термодинамика химического равновесия» и «Фазовые равновесия», изучение которых является важнейшей практической задачей физической химии. Руководство состоит из пяти тем и включает 22 задачи, для каждой из которых предусмотрено 30 вариантов индивидуальных заданий. Задачи направлены на развитие научной интуиции, воображения и способствуют более глубокому пониманию предмета. В каждой теме кратко излагаются основные физико-химические понятия и законы, приведены необходимые для решения уравнения. Для каждой задачи дан пример с подробным решением. Руководство построено таким образом, что решение предыдущего задания является частью решения последующего, т.е. задания представлены в логичной последовательности и иллюстрируют связь полученных физико-химических результатов с фундаментальными законами химической термодинамики. Материал каждой темы представлен в следующей последовательности: 1) условие задач; 2) пример решения задач; 3) многовариантные задачи для самостоятельного решения; 4) контрольные вопросы. Такая форма изложения является оптимальной для проведения практических занятий по физической химии и должна помочь студентам освоить основные термохимические расчеты. Тема 1. Расчет теплот физических и химических превращений Задача №1
Вещество А (табл.1) в количестве m г находится при T = 25 ºС и давлении p1 = 1,013 ·105 Па. Определить теплоту Q, работу A, изменение внутренней энергии DU и изменение энтальпии DH: а) при изотермическом расширении до объема V2 м3; б) при изобарном расширении до того же объема; в) при изохорном нагревании до достижения давления p2 Па; г) при адиабатическом сжатии до p2 Па. Принять, что вещество А подчиняется законам идеальных газов. Истинную мольную теплоемкость вещества взять из справочника.
Таблица 1
Продолжение таблицы1
Решение:
Для двуокиси углерода CO2 в количестве 100 г, находящейся при температуре T = 0 ºС и давлении p = 1,013 ·105 Па, определим Q, A, DU и DH: а) при изотермическом расширении до объема 0,2 м3; б) при изобарном расширении до того же объема; в) при изохорном нагревании до достижения давления 2,026 ·105 Па; г) при адиабатическом сжатии до 2,026 ·105 Па. Математическое выражение I-го закона термодинамики для процессов, связанных с бесконечно малыми изменениями состояния системы, имеет вид
где Q – теплота; U – внутренняя энергия; A – работа. Функции, которые однозначно определяют состояние системы, называют функциями состояния. Внутренняя энергия U, а также энтальпия H, которая выражается уравнением
являются функциями состояния. Теплота Q и работа A служат формами передачи энергии и связаны с процессом, а не с состоянием системы, т.е. являются функциями процесса. В двух частных случаях теплота и работа приобретают свойства функций состояния (закон Гесса):
В интегральной форме математическое выражение I-го закона термодинамики имеет вид
Для решения задачи примем, что CO2 подчиняется законам идеальных газов, а истинная мольная теплоемкость CO2 при постоянном давлении постоянна и равна 37,1 Дж/моль·К.
а) для изотермического расширения ∆U = 0 и ∆H = 0, следовательно Q = A. Если из всех внешних сил на систему действует только внешнее давление p, то при переходе системы из состояния 1 в состояние 2 работу расширения можно вычислить по уравнению
Для изотермического процесса
Определим число молей CO2 по формуле
Число молей CO2 в 100 г составляет n = 100/44 = 2,27 моль. Первоначальный объем определяем из уравнения Клапейрона – Менделеева
Количество теплоты и работы определяем по уравнению (7)
Q = A = 2,3·2,27·8,314·273 lg (0,2/0,0509) = 7070 Дж = 7,07 кДж.
б) для изобарного процесса
Отсюда Qp = ∆H = 2,27·37,1·273/0,0509 (0,2 – 0,0509) = 67400 Дж = = 67,4 кДж.
Работа расширения газа в изобарных условиях
A = 1,013·105 (0,2 – 0,0509) = 15000 Дж = 15,0 кДж.
Из уравнения (5)
в) для изохорного процесса
Выражение для взаимосвязи мольной теплоемкости идеальных газов при постоянном давлении Сp и при постоянном объеме CV имеет вид
Теплоемкость при постоянном объеме
CV = Cp – R = 37,1 – 8,31 = 28,8 Дж/моль·К.
QV = ∆U = 2,27·28,8·273/1,013·105 (2,026 ·105 – 1,013·105) = 17900 Дж = = 17,9 кДж.
Из уравнения (2) для изохорного процесса имеем:
Отсюда
∆H = 17,9 + 0,0509 (2,026 – 1,013) · 105 = 23100 Дж = 23,1 кДж. г) для адиабатического сжатия Q = 0 и A = – ∆U
где
Из уравнения (2) для адиабатического процесса
Выражая конечный объем V2 из уравнения адиабаты
Задача №2
Определите тепловой эффект реакции, приведенной в табл. 2, при T = 298 Ки р = 1,0133·105 Па: а) по стандартным теплотам образования исходных и конечных веществ; б) по стандартным теплотам сгорания исходных и конечных веществ. Таблица 2
Решение: Решение задачи рассмотрим на примере реакции синтеза аммиака:
а) Согласно следствию из закона Гесса, тепловой эффект реакции при стандартных условиях равен разности сумм стандартных теплот образования продуктов и исходных веществ:
где Воспользуемся справочником физико-химических величин (табл.3):
Таблица 3
б) Для реакций, протекающих с участием органических веществ, тепловой эффект реакции при стандартных условиях можно определять и по стандартным теплотам сгорания как разность сумм стандартных теплот сгорания исходных веществ и продуктов реакции:
в) При отсутствии данных о теплотах образования или сгорания веществ, участвующих в реакции, можно вычислить тепловой эффект реакции, используя для этого методы приближенного расчета тепловых эффектов, например, по энергиям химических связей. В этом методе расчета сначала предполагают разложение исходных простых веществ на атомы, а затем образование из них конечного газообразного соединения. Первый этап связан с затратой энергии на разрыв связей в исходных простых веществах, а второй – с выделением энергии образования новых связей. Поэтому тепловой эффект реакции может быть определен по уравнению
где n – число связей данного вида; ε – энергия разрыва или образования связей; n* – число атомов твердых элементов; Qвозг – теплота возгонки твердого элемента..
Задача №3
Определите, насколько отличается тепловой эффектпри постоянном давлении
Решение: Решение задачи рассмотрим на примере реакции синтеза аммиака:
Из первого закона термодинамики (1) для случая, когда в системе не совершается других видов работы, кроме работы расширения,
Изменение внутренней энергии и изменение энтальпии связаны формулами:
или
где Dn – изменение числа молей газообразных продуктов в ходе реакции. Таким образом, соотношение ∆H и ∆U определяетсязнаком Dn. Для реакции
Dn = (2) – (1 + 3) = – 2;
Dn < 0, следовательно DH < DU. Определим разницу ∆H – ∆U при T=298 К:
∆H – ∆U = DnRT =
= (–2)·8,314 Дж/(моль·К)·298К = – 4955,14 Дж = – 4,96 кДж.
Задача №4
Определите стандартную теплоту образования соединения (табл. 4) из простых веществ, если известна его теплота сгорания при температуре Т =298 К и давлении р = 1,0133·105 Па. Принять, что продуктами сгорания являются CO2 (Г), H2О (Ж), и N2 (Г). Использовать известные теплоты сгорания простых веществ:
Таблица 4
Продолжение таблицы 4
* Продукты сгорания: CO2 (Г), Cl2(Ж) и HCl (Р-Р); ** Продукты сгорания: CO2 (Г), H2О(Ж) и HCl (Р-Р). Решение: Вычислим стандартную теплоту образования карбамида
Для решения задачи применим метод комбинирования термохимических уравнений. Воспользуемся изменениями энтальпий следующих реакций: (а) (b) (c) Необходимая нам реакция образования карбамида из простых веществ получается при сложении термохимических уравнений (b) и (c), за вычетом уравнения (а). Уравнение (c) необходимо умножить на коэффициент 2. Следовательно,
Справочная величина теплоты образования карбамида
Задача №5
Рассчитайте теплоту сгорания газообразного вещества, если известна теплота сгорания данного вещества в жидком агрегатном состоянии и его мольная теплота испарения. Теплоту сгорания жидкого вещества возьмите в табл. 4, температуру кипения – из табл.5. Мольную теплоту испарения рассчитайте по формуле:
Таблица 5
Продолжение таблицы 5
Решение: Определим теплоту сгорания газообразного пропана, если известна теплота сгорания жидкого пропана (DH1= –2200 кДж/моль) и мольная теплота испарения жидкого пропана (DH2 = 20 кДж/моль). Для этого воспользуемся методом составления циклов из реакций с известной и неизвестной энтальпиями. Составим термохимическую схему:
Рис. 1 - Термохимическая схема
Переход из начального состояния «газообразный пропан» в конечное состояние «продукты сгорания» можно совершить как напрямую, так и через промежуточное состояние «жидкий пропан». Согласно закону Гесса тепловой эффект не зависит от пути протекания процесса. Тепловой эффект перехода «газ–жидкость» равен по величине, но обратен по знаку тепловому эффекту перехода «жидкость-газ».
ΔН3 = –ΔН2 + ΔН1 = –20 + (–2200) = –2220 кДж/моль.
Тема 2. Расчет тепловых эффектов химических реакций при различных температурах Задача №6
Вычислите среднюю теплоемкость
Таблица 6
Решение: Рассмотрим расчет средней теплоемкости аммиака в интервале температур от 298 до 800К. Теплоемкость – это отношение количества теплоты, поглощаемой телом при нагревании, к повышению температуры, которым сопровождается нагревание. Для индивидуального вещества различают удельную (одного килограмма) и мольную (одного моля) теплоемкости. Истинная теплоемкость
где δQ – бесконечно малое количество теплоты, необходимое для повышения температуры тела на бесконечно малую величину dT . Средняя теплоемкость – это отношение количества теплоты Q к повышению температуры ∆T = T2 – T1,
Поскольку теплота не является функцией состояния и зависит от пути процесса, необходимо указывать условия протекания процесса нагревания. В изохорном и изобарном процессах для бесконечно малого изменения δQV = dU и δQp = dH, поэтому
Связь между истинными изохорной (СV) и изобарной (Cp) теплоемкостями вещества и его средними изохорной
Зависимости истинной теплоемкости от температуры выражаются следующими эмпирическими уравнениями:
Воспользуемся справочником физико-химических величин. Выпишем коэффициенты (a, b, c) уравнения зависимости изобарной теплоемкости аммиака от температуры:
Таблица 7
Запишем уравнение зависимости истинной теплоемкости аммиака от температуры:
Подставим это уравнение в формулу (24) и вычислим среднюю теплоемкость аммиака:
= 0,002 [29,8(800–298) + 25,5·10–3/2 (8002 – 2982) +
+ 1,67·105 (1/800 – 1/298)] = 43,5 Дж/моль·К.
Задача №7
Для химической реакции, приведенной в табл. 2, постройте графики зависимостей суммы теплоемкостей продуктов реакции от температуры Решение:
Рассчитаем изменение теплоемкости при температурах 298 К, 400 К и 600 К на примере реакции синтеза аммиака:
Выпишем коэффициенты (a, b, c, с/)[1] уравнений зависимости истинной теплоемкости аммиака от температуры для исходных веществ и продуктов реакции с учетом стехиометрических коэффициентов
Сумма коэффициентов а для продуктов реакции равна
Таблица 8
Таким образом, уравнение зависимости
Для построения графика зависимости суммы теплоемкости продуктов реакции от температуры При Т = 298 К
При Т= 400 К При Т = 600 К Уравнение зависимости
Аналогично рассчитываем При Т=298 К
При Т = 400 К При Т = 600 К Далее рассчитываем изменение изобарной теплоемкости
По рассчитанным значениям строим графики зависимостей суммы теплоемкостей продуктов реакции и суммы теплоемкостей исходных веществ от температуры.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (1)
, (1) , (2)
, (2) ; (V = const, T = const) (3)
; (V = const, T = const) (3) . (p = const, T = const) (4)
. (p = const, T = const) (4)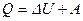 . (5)
. (5) . (6)
. (6) . (7)
. (7) . (8)
. (8) , (9)
, (9) = 2,27·8,314·273/1,013·105 = 0,0509 м3.
= 2,27·8,314·273/1,013·105 = 0,0509 м3. . (10)
. (10) , (11)
, (11) = 67,4 – 15,0 = 52,4 кДж.
= 67,4 – 15,0 = 52,4 кДж. . (12)
. (12)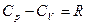 . (13)
. (13) .
. , (14)
, (14) = 37,1/28,8 = 1,29.
= 37,1/28,8 = 1,29. = – 970 Дж = – 2,97кДж.
= – 970 Дж = – 2,97кДж.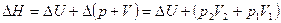 .
. , получим
, получим , (15)
, (15) = 3830 Дж = 3,83кДж.
= 3830 Дж = 3,83кДж.






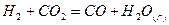





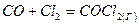









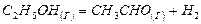





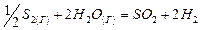
 .
.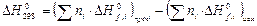 , (16)
, (16)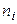 – стехиометрические коэффициенты веществ в уравнении реакции.
– стехиометрические коэффициенты веществ в уравнении реакции. , кДж/моль
, кДж/моль
 ,
, = 2·(–45,94) – (0 + 3·0) = –91,88 кДж.
= 2·(–45,94) – (0 + 3·0) = –91,88 кДж. . (17).
. (17). , (18)
, (18) от теплового эффекта при постоянном объеме
от теплового эффекта при постоянном объеме  при T = 298 К дляреакции, приведенной в табл. 2.
при T = 298 К дляреакции, приведенной в табл. 2. ;
;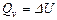 .
. , (19)
, (19) , (20)
, (20)
 DН= – 393,795 кДж/моль;
DН= – 393,795 кДж/моль; DН= – 286,043 кДж/моль.
DН= – 286,043 кДж/моль. , кДж/моль
, кДж/моль
 нитрометан
нитрометан
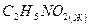 нитроэтан
нитроэтан
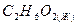 этиленгликоль
этиленгликоль
 глицерин
глицерин
 диметиламин
диметиламин
 ацетон
ацетон
 циклогексан
циклогексан
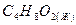 этилацетат
этилацетат
 пропанол-1
пропанол-1
 этанол
этанол
 амиловый спирт
амиловый спирт
 муравьиная кислота
муравьиная кислота
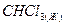 * хлороформ
* хлороформ
 анилин
анилин
 диэтиловый эфир
диэтиловый эфир
 пиридин
пиридин
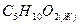 валериановая кислота
валериановая кислота
 толуол
толуол
 октан
октан
 муравьиная кислота
муравьиная кислота
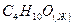 бутанол
бутанол
 ** хлорметан
** хлорметан
 пентан
пентан
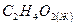 уксусная кислота
уксусная кислота
 нитробензол
нитробензол
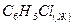 ** хлорбензол
** хлорбензол
 м-ксилол
м-ксилол
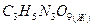 нитроглицерин
нитроглицерин
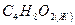 1,4-диоксан
1,4-диоксан
 бензол
бензол
 . По определению теплота образования – это тепловой эффект реакции образования одного моля вещества из простых веществ при стандартных условиях. Следовательно, в задаче требуется найти тепловой эффект реакции:
. По определению теплота образования – это тепловой эффект реакции образования одного моля вещества из простых веществ при стандартных условиях. Следовательно, в задаче требуется найти тепловой эффект реакции: +
+  .
. , DН1= –634,749 кДж/моль.
, DН1= –634,749 кДж/моль. , DН2= – 393,795 кДж/моль.
, DН2= – 393,795 кДж/моль. , DН3= – 286,043 кДж/моль.
, DН3= – 286,043 кДж/моль.
 , Дж/(моль·К)
, Дж/(моль·К) амиловый спирт
амиловый спирт
 пиридин
пиридин

 вещества, приведенного в табл. 6, в интервале температур от 298 до Т К.
вещества, приведенного в табл. 6, в интервале температур от 298 до Т К.
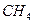

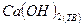
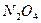
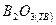


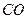


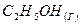








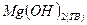


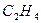


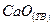

 , (21)
, (21) .
. и
и  . (22)
. (22) теплоемкостями в интервале температур от Т1 до Т2 выражается уравнениями (23) и (24):
теплоемкостями в интервале температур от Т1 до Т2 выражается уравнениями (23) и (24): ; (23)
; (23) . (24)
. (24) ; (для неорганических веществ) (25)
; (для неорганических веществ) (25) . (для органических веществ) (26)
. (для органических веществ) (26)
 .
. = 1/(800-298)
= 1/(800-298)  =
=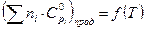 и суммы теплоемкостей исходных веществ от температуры
и суммы теплоемкостей исходных веществ от температуры  . Уравнения зависимости
. Уравнения зависимости 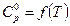 возьмите из справочника. Рассчитайте изменение теплоемкости в ходе химической реакции (
возьмите из справочника. Рассчитайте изменение теплоемкости в ходе химической реакции (  ) при температурах 298 К, 400 К и Т К (табл. 6).
) при температурах 298 К, 400 К и Т К (табл. 6). .
. = 27,88 + 3·27,28 = 109,72.
= 27,88 + 3·27,28 = 109,72. = 2·29,8 = 59,6.
= 2·29,8 = 59,6. =
=  =59,6 – 109,72 = –50,12.
=59,6 – 109,72 = –50,12. ,
,  ,
,  )
) 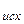

 ,
, 

 для продуктов реакции имеет следующий вид:
для продуктов реакции имеет следующий вид: = 59,60 + 50,96·10–3Т – 3,34·105/Т2.
= 59,60 + 50,96·10–3Т – 3,34·105/Т2. = 59,60 + 50,96·10–3 · 298 – 3,34·105/2982 = 71,03 Дж/К;
= 59,60 + 50,96·10–3 · 298 – 3,34·105/2982 = 71,03 Дж/К; = 77,89 Дж/К;
= 77,89 Дж/К;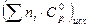 = 109,72 + 14,05·10–3Т + 1,50·10-5/Т2.
= 109,72 + 14,05·10–3Т + 1,50·10-5/Т2. исходных веществ при нескольких температурах:
исходных веществ при нескольких температурах: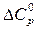 в ходе реакции при нескольких температурах:
в ходе реакции при нескольких температурах: = –50,12 + 36,91·10–3Т – 4,84·105/Т2,
= –50,12 + 36,91·10–3Т – 4,84·105/Т2, = –44,57 Дж/К;
= –44,57 Дж/К; = –38,39 Дж/К;
= –38,39 Дж/К; = –29,32 Дж/К.
= –29,32 Дж/К. 