
|
|
Транспортная задача на минимумМетод сечения Гомори Допустим мы решали задачу и получили последнюю таблицу без учета целочисленности
Если βi – целые, то задача решена; иначе выбирают βi с наибольшей дробной частью и выписывают уравнение из таблицы.
По условию целочисленности xi, ωi – целые.
Чтобы уравнять обе части мы добавляем искусственную переменную
К полученной таблице добавляется строка, соответствующая отсечению Гомори, в столбце Xопт стоит – fi (т.е. отрицательное число). А так как в столбце Xопт стоит отрицательное число – поэтому применяем двойственный симплекс-метод. пример. max z = 7x1 + 9x2.
Итак, x1 = 4; x2 = 3; max z = 55; s1 = 1; s2 = 4; R1 = 0; R2 = 0. Транспортная задача на минимум пример. На трех базах Б1; Б2; Б3 находится однородный груз. Этот груз необходимо доставить в пять пунктов П1, П2, ... , П5. Запасы груза на трех базах ai и потребности пунктов bj указаны в таблице. Стоимость перевозки одной тонны груза с базы Бi в пункт Пj (Бi → Пj) равная cij рублей. Спланировать их перевозки так, чтобы их стоимость была наименьшей.
1 способ. Симплекс метод xij – перевозка Бi → Пj
2 способ. Метод потенциалов 1 этап. Составить начальный план. Показатели плана записываются только в клетки с оценками, xij ³ 0. Для построения начального решения используются следующие методы. 1 метод – Метод северо-западного угла Заполняют верхнюю левую клетку, записывая туда максимально возможное значение, затем переходят к соседней клетке.
Показатель левой верхней клетки выбирается равным наименьшему значению из заданных сумм по первой строке и по первому столбцу. Дальше заполняется соседняя клетка. 2 метод – минимальный элемент по строке
Сначала заполняется первая строка, для этого в ней выбирается клетка с минимальной стоимостью перевозки и заполняется максимально возможным значением. Затем переходят к клетке со следующей по величине стоимостью перевозки и т.д., пока не будет исчерпан запас первой строки. Затем переходят ко второй строке, процесс повторяется. 3 метод – минимальный элемент по столбцу. Аналогично вышеизложенному. 4 метод – метод минимального элемента.
Выбираем наименьший элемент по стоимости по всей таблице. Ставим туда максимально возможное значение. 2 этап. Проверка плана на оптимальность. Пусть таблица содержит m строк и n столбцов. Полученный начальный план называется невырожденным, если число его заполненных клеток не меньше, чем m + n – 1. Рассмотрим план северо-западного угла. Заполненных клеток 7. m + n – 1 = 5 + 3 – 1 = 7 Þ план невырожденный. В этом случае система потенциалов строится таким образом. αi – потенциалы строк. βj – потенциалы столбцов. Положим α1 = 0, остальные потенциалы считают из условия: для заполненных клеток cij = αi + βj.
Отступление.Для вырожденного плана. например:
В свободные клетки с наименьшей стоимостью, для которой потенциал еще не просчитан ставим ноль (т.е. появляется нулевая перевозка) клетка становится условно заполненной. Условие оптимальности плана cij ³ αi + βj – признак оптимальности плана. Так как для занятых клеток условие выполняется по построению потенциалов, то проверяем только свободные. cij –(αi + βj) ³ 0
Значит план неоптимален, его надо улучшать. 3 этап. Построение цикла перевозки. Здесь мы выбираем самую плохую клетку Б3П3, в нее помещаем вершину. Цикл – это прямоугольник, начальная вершина которого находится в самой плохой клетке, а остальные вершины только в заполненных клетках. Начальная вершина отмечается знаком «плюс» (+), далее в порядке чередования ставятся знаки «–», «+». Выберем объем дополнительной перевозки – это будет минимальная перевозка, отмеченная знаком «–». θ = min (285; 660) = 285. Прибавим её в клетках со знаком «+» и отнимем в клетках со знаком «–». Таким образом мы пересчитаем план и все начнется сначала.
θ = min (525; 375; 810) = 285.
θ = min (150; 435) = 150.
θ = min (705; 285; 420) = 285.
с = 420 · 5 + 285 · 6 + 135 · 7 + 435 · 6 +660 · 5 + 555 · 5 + 810 · 3 = 15870. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|






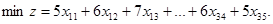
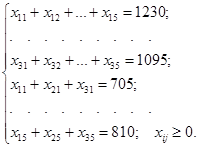


 Б1
Б1
 Б1
Б1
 Б2
Б2
 Б1
Б1
 Б2
Б2