
|
|
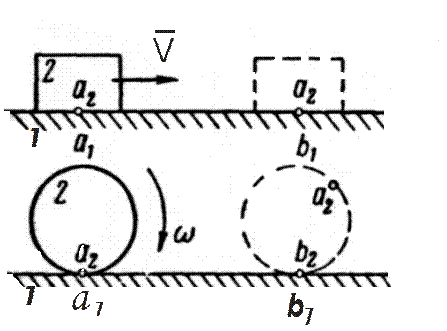
Трение скольжения во вращательной кинематической пареТрение 1 Виды трения При всяком относительном движении двух соприкасающихся тел на поверхности их соприкосновения возникает сила трения, направленная противоположно скорости относительного движения и сопротивляющаяся ему. Различают в основном два вида трения: трение скольжения (рис. 6.1,а) и трение качения (рис.6.1,б).
а)
Рис.6.1
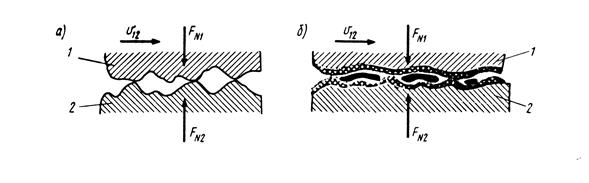
Трение скольжения может быть нескольких видов: сухое, жидкостное или полужидкостное. При сухом трении между трущимися поверхностями совершенно нет смазки (рис.6.2,а). При жидкостном трении смазка полностью разделяет трущиеся поверхности. Если смазывающая жидкость не полностью разделяет трущиеся поверхности, то трение будет полужидкостным( рис.6.2,б).
Рис.6.2
Смазка значительно уменьшает силы трения. Основные закономерности трения скольжения
Пусть тело 1, прижимаемое к телу 2 силой
Рис.6.3 Сила трения F направлена противоположно относительному движению и пропорциональна нормальной реакции N.
где Сложим силу трения
Из уравнения (1) следует
тогда
Угол
Трение по наклонной плоскости
Случай 1. Тело движется вверх по наклонной плоскости под действием горизонтальной силы
Рис.6.4 Кроме этих сил, на тело будет действовать реакция со стороны наклонной плоскости
На рис 3,б по этому уравнению построен план сил, из которого следует что сила
Случай 2. Тело движется вниз по наклонной плоскости под действием вертикальной движущей силы
Рис.6.5 При равномерном движении
На рис 4,б по этому уравнению построен план сил, из которого следует, что сила . Из уравнения (5) видно, что если угол
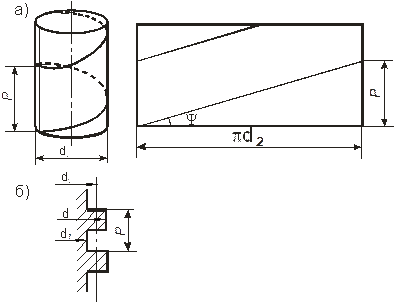
Трение в винтовой кинематической паре Движение гайки относительно винта можно приближенно рассматривать как движение тела по наклонной плоскости с углом наклона, равным углу подъема средней винтовой линии резьбы. На рис.6.6 показана схема движения гайки по винтовой поверхности резьбы винта.
Рис.6.6 Пусть гайка нагружена вертикальной силой
Угол подъема средней винтовой линии
Рис.6.7
где
Усилие в винтовых передачах обычно прикладывают не по среднему диаметру
или
Трение скольжения во вращательной кинематической паре Пусть опорная часть вала – цапфа, вращающаяся в подшипнике скольжения, прижимается к подшипнику силой
Рис.6.8 Складывая нормальную реакцию Фиктивные коэффициенты трения будут равны: Для не приработавшихся цапф Для приработавшихся цапф Фиктивный угол трения
Реакция
направленной противоположно движущему моменту
где Так как угол трения очень мал, то
Следовательно
Тогда момент сил трения равен
Итак, полная реакция
Трение качения Пусть цилиндр (или шар), на который действует вертикальная нагрузка
Рис 6.9
В действительности реальные тела всегда подвергаются упругим и пластическим деформациям. Если цилиндр, на который действует сила Если теперь к цилиндру приложить силу
Движущий момент
Для равномерного качения необходимо, чтобы движущий момент был равен моменту сопротивления качению
откуда необходимая движущая сила
Величина Обычно сопротивление качению значительно меньше, чем сопротивление трения скольжения.
Коэффициент полезного действия механизмов В процессе передачи сил от начального звена к рабочему органу машины часть работы расходуется на преодоление полезных сопротивлений (т.е. тех, для преодоления которых создана машина), а часть – на преодоление вредных сопротивлений (т.е. сил трения, аэродинамических сопротивлений, сопротивлений смазывающей жидкости и т. д.).
где
Механическим коэффициентом полезного действия (КПД) называется отношение работы сил полезного сопротивления к работе движущих сил:
где Поскольку ни в одном механизме Каждая машина представляет собой комплекс механизмов, соединенных последовательно или параллельно между собой. Поэтому общий КПД машины можно вычислить по отдельным ее элементам в зависимости от их соединения.
1 Последовательное соединение механизмов:
Здесь
Общий КПД определяется по формуле:
Найдем произведение частных КПД механизмов, входящих в состав агрегата:
Сравнивая (23) и (22) видно, что при последовательном соединении отдельных механизмов в агрегат общий КПД равен произведению КПД отдельных механизмов, составляющих данный агрегат:
2. Параллельное соединение механизмов:
Работа движущих сил распределяется на 3 потока. Общий КПД:
, (6.20)
где
Общий КПД агрегата определяется по формуле:
В частном случае, когда КПД всех механизмов одинаковы, общий КПД равен любому частному
При равных условиях параллельное соединение механизмов обеспечивает более высокий КПД, чем последовательное.
Явление самоторможения При подсчете КПД может быть случай, когда он оказывается отрицательным:
Это возможно лишь в том случае, когда работа движущих сил меньше работы сил вредных сопротивлений. Естественно, что машина в таком случае двигаться не может. Механизм при отрицательном КПД не только не может совершать полезной работы, но нужна еще дополнительная затрата работы движущих сил, чтобы механизм вообще мог двигаться. Механизмы, которые не могут двигаться без дополнительной затраты работы движущих сил даже при отсутствии сил полезных сопротивлений, называются самотормозящими механизмами. Самотормозящие механизмы имеют широкое применение, особенно в различных подъемных устройствах. Однако необходимо отметить, что КПД самотормозящих механизмов всегда меньше 0,5. Поэтому самотормозящие механизмы обычно применяются при небольших мощностях и кратковременной работе механизма.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Q, движется относительно него под действием горизонтальной силы Р (рис. 6. 2).Тогда на поверхности соприкосновения возникает сила трения F, приложенная к телу 1 и препятствующая его движению. Между телами 1 и 2 возникает нормальная реакция N.
Q, движется относительно него под действием горизонтальной силы Р (рис. 6. 2).Тогда на поверхности соприкосновения возникает сила трения F, приложенная к телу 1 и препятствующая его движению. Между телами 1 и 2 возникает нормальная реакция N.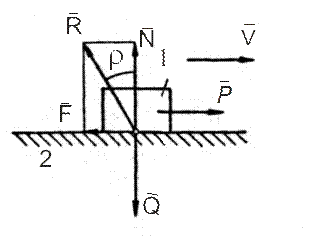
 ,. (6.1)
,. (6.1)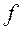 – коэффициент трения.
– коэффициент трения. с нормальной реакцией
с нормальной реакцией  звена 2 на звено 1, возникающей в результате действия силы
звена 2 на звено 1, возникающей в результате действия силы  . Полученная полная реакция
. Полученная полная реакция  отклонена от нормали на угол
отклонена от нормали на угол  . Тангенс этого угла равен
. Тангенс этого угла равен (6.2)
(6.2)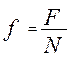 ,
, . (6.3)
. (6.3)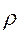 отклонения реакции от нормали называется углом трения.
отклонения реакции от нормали называется углом трения. Рассмотрим различные случаи движения тела по наклонной плоскости с углом наклона
Рассмотрим различные случаи движения тела по наклонной плоскости с углом наклона  .
. , являющейся движущей силой, и вертикальной силы
, являющейся движущей силой, и вертикальной силы 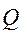 , являющейся силой сопротивления (рис.6.4, а).
, являющейся силой сопротивления (рис.6.4, а).
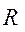 , которая отклонена от нормали
, которая отклонена от нормали  в сторону, противоположную движению на угол трения
в сторону, противоположную движению на угол трения  .
. (6.4)
(6.4)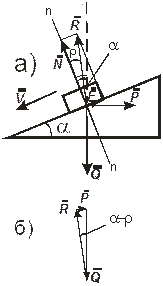
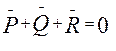
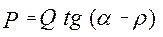 . (6.5)
. (6.5)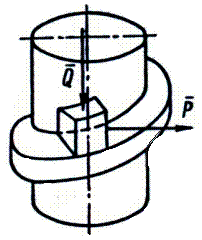
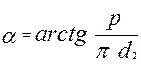 , (6.6)
, (6.6) - шаг резьбы;
- шаг резьбы;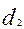 =
=  - средний диаметр резьбы;
- средний диаметр резьбы; - наружный диаметр резьбы;
- наружный диаметр резьбы; - внутренний диаметр резьбы (рис 10, б).
- внутренний диаметр резьбы (рис 10, б).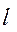 (длина гаечного ключа) или прикладывают крутящий момент. Этот момент равен
(длина гаечного ключа) или прикладывают крутящий момент. Этот момент равен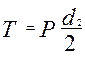 (6.7)
(6.7) . (6.8)
. (6.8)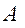 при этом будет действовать нормальная реакция
при этом будет действовать нормальная реакция 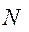 , являющейся равнодействующей всех элементарных сил давлений, распределенных на поверхности соприкосновения цапфы и подшипника. В этой же точке
, являющейся равнодействующей всех элементарных сил давлений, распределенных на поверхности соприкосновения цапфы и подшипника. В этой же точке 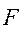 , направленная по касательной к окружности цапфы против вращения.
, направленная по касательной к окружности цапфы против вращения.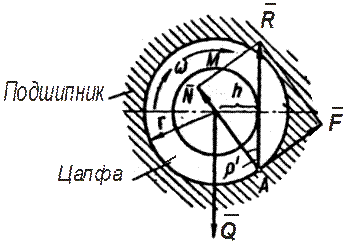
 . Этот фиктивный (приведенный) угол трения отличается от действительного
. Этот фиктивный (приведенный) угол трения отличается от действительного 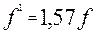 ;
; .
.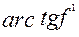 .
. ,
,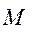 . Величина плеча
. Величина плеча  , как видно из рисунка, равна
, как видно из рисунка, равна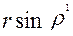 ,
, -радиус опорной части вала.
-радиус опорной части вала. .
. . (6.9)
. (6.9)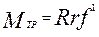 (6.10)
(6.10)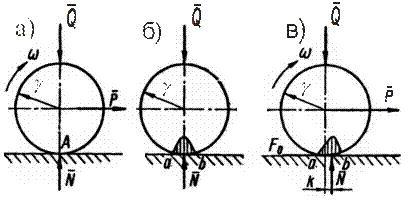
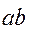 (рис.6.9,б) возникают деформации и напряжения, которые распределяются по некоторому закону. При неподвижном цилиндре кривая распределения напряжений симметрична относительно диаметра.
(рис.6.9,б) возникают деформации и напряжения, которые распределяются по некоторому закону. При неподвижном цилиндре кривая распределения напряжений симметрична относительно диаметра. .Таким образом, возникает пара сил
.Таким образом, возникает пара сил 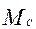 , равный
, равный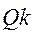 . (6.11)
. (6.11) , создаваемый парой сил
, создаваемый парой сил  . (6.12)
. (6.12)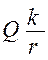 . (6.13)
. (6.13) , (6. 14)
, (6. 14) - работа движущих сил;
- работа движущих сил;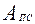 - работа сил полезного сопротивления;
- работа сил полезного сопротивления; - работа сил вредных сопротивлений.
- работа сил вредных сопротивлений.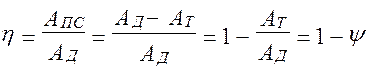 , (6.15)
, (6.15) - коэффициент потерь, который показывает, какая часть работы движущих сил расходуется на преодоление внепроизводственных сопротивлений.
- коэффициент потерь, который показывает, какая часть работы движущих сил расходуется на преодоление внепроизводственных сопротивлений.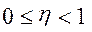 . Чем выше КПД, тем совершеннее машина в энергетическом отношении. Сравнение по КПД имеет смысл только для однотипных машин.
. Чем выше КПД, тем совершеннее машина в энергетическом отношении. Сравнение по КПД имеет смысл только для однотипных машин.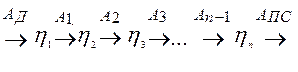 .
.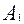 - работа сил полезного сопротивления 1-го механизма и движущих сил 2-го механизма;
- работа сил полезного сопротивления 1-го механизма и движущих сил 2-го механизма;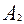 … - работа сил полезного сопротивления 2 – го механизма и движущих сил 3-го механизма….
… - работа сил полезного сопротивления 2 – го механизма и движущих сил 3-го механизма…. (6.16)
(6.16) . (6.17)
. (6.17)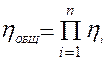 . (6.18)
. (6.18)
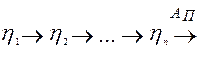
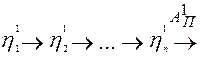

 .
.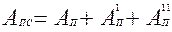 , (6.19)
, (6.19)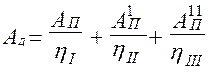
 ,
,  ,
,  - соответственно общие КПД потоков, на которые распределяется энергия.
- соответственно общие КПД потоков, на которые распределяется энергия. ,
, ,
, . (6.21)
. (6.21)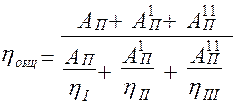 (6.22)
(6.22)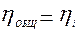 (6.23)
(6.23) (6.24)
(6.24)