
|
|
Координаты центров тяжести неоднородных тел.12 Лекция 4. Центр тяжести. В данной лекции рассматриваются следующие вопросы 1. Сложение параллельных сил. Центр параллельных сил. 2. Параллельные силы, распределенные по отрезку прямой. 3. Центр тяжести твердого тела. 4. Координаты центров тяжести неоднородных тел. 5. Координаты центров тяжести однородных тел. 6. Способы определения координат центров тяжести. 7. Центры тяжести некоторых однородных тел. Изучение данных вопросов необходимо в дальнейшем для изучения динамики движении тел с учетом трения скольжения и трения качения, динамики движения центра масс механической системы, кинетических моментов, для решения задач в дисциплине «Сопротивление материалов». Сложение параллельных сил. Центр параллельных сил. Пусть даны две параллельные силы
Рис.34
Конечно, величина их равнодействующей Значит Отсюда Если параллельные силы направлены в противоположные стороны (рис.35), то аналогично можно доказать, что равнодействующая по величине будет равна разности сил:
Рис.35
Следует заметить, что если точка приложения равнодействующей расположена на одной прямой с точками Такая точка приложения равнодействующей называется центром параллельных сил. Конечно, если хотя бы одну из сил перенести по своей линии действия в другую точку, то и точка приложения равнодействующей, центр параллельных сил, тоже переместится по линии действия. Следовательно, положение центра параллельных сил зависит от координат точек приложения сил. Центром нескольких параллельных сил, найденный последовательным сложением каждых двух сил, будем называть точку С, радиус-вектор которой определяется формулой
Используя (1), нетрудно найти координаты центра параллельных сил. Если радиусы-векторы откладывать из начала координат, то проекции радиусов-векторов точек на оси будут равны их координатам. Поэтому, проектируя векторное равенство (1) на оси, получим
где Параллельные силы, распределенные по отрезку прямой.
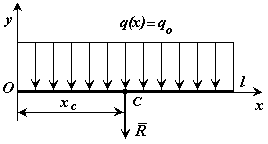
а) общий случай
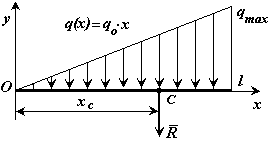
Распределенная по отрезку прямой сила интенсивности Сосредоточенная сила прикладывается в точке С (центре параллельных сил) с координатой
б) постоянная интенсивность
в) интенсивность, меняющаяся по линейному закону
Центр тяжести тел. На все точки тела, находящегося вблизи поверхности Земли, действуют силы – силы тяжести этих точек или их вес Центр этих параллельных сил, сил тяжести точек, называется центром тяжести тела. Значит находить центр тяжести тел можно как центр параллельных сил. Например, координаты его
где
Рис.36
При определении центра тяжести полезны несколько теорем. 1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой плоскости. Если оси х и у расположить в этой плоскости симметрии (рис.36), то для каждой точки с координатами
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Действительно, в этом случае, если ось z провести по оси симметрии, для каждой точки с координатами
Аналогично доказывается и третья теорема. 3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
И ещё несколько замечаний. Первое. Если тело можно разделить на части, у которых известны вес и положение центра тяжести, то незачем рассматривать каждую точку, а в формулах (2) Второе. Если тело однородное, то вес отдельной части его
И аналогично, Третье замечание. Если тело состоит из однородных пластин одинаковой, малой толщины, то объём каждой пластины
где Четвёртое замечание. Если тело состоит из стержней, прямых или криволинейных, однородных и постоянного сечения, то вес их
где Отметим, что согласно определению центр тяжести - это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).
Координаты центров тяжести неоднородных тел. Координаты центра тяжести неоднородного твердого тела в выбранной системе отсчета определяются следующим образом:
где
Если твердое тело представляет собой неоднородную поверхность, то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:
где
Если твердое тело представляет собой неоднородную линию, то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:
где

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
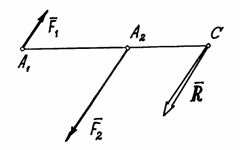
и  , направленные в одну сторону и приложенные к точкам
, направленные в одну сторону и приложенные к точкам  и
и  (рис.34).
(рис.34).
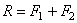 . Вектор её параллелен силам и направлен в ту же сторону. С помощью теоремы Вариньона найдём точку приложения равнодействующей – точку С. По этой теореме
. Вектор её параллелен силам и направлен в ту же сторону. С помощью теоремы Вариньона найдём точку приложения равнодействующей – точку С. По этой теореме 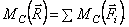
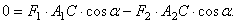
 То есть точка приложения равнодействующей делит расстояние между точками
То есть точка приложения равнодействующей делит расстояние между точками  (если
(если  ), параллельна им, направлена в сторону большей силы и расположена за большей силой – в точке С. А расстояния от точки С до точек приложения сил обратно пропорциональны силам:
), параллельна им, направлена в сторону большей силы и расположена за большей силой – в точке С. А расстояния от точки С до точек приложения сил обратно пропорциональны силам: 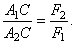
 , (1)
, (1)
 - радиусы-векторы точек приложения сил;
- радиусы-векторы точек приложения сил;  – величина равнодействующей параллельных сил, равная алгебраической сумме этих сил (знак силы определяется направлением, которое заранее выбирается и считается положительным).
– величина равнодействующей параллельных сил, равная алгебраической сумме этих сил (знак силы определяется направлением, которое заранее выбирается и считается положительным).
 – координаты точек приложения сил.
– координаты точек приложения сил.
 - интенсивность распределенной силы [Н/м],
- интенсивность распределенной силы [Н/м], - элементарная сила.
- элементарная сила.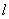 – длина отрезка
– длина отрезка .
.

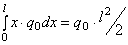
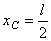
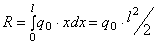
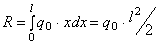
 .
. . Вообще эти силы будут сходящимися – линии действия их пересекаются в центре Земли. Но, если пренебречь размерами тела в сравнении с размерами Земли, то можно считать их параллельными.
. Вообще эти силы будут сходящимися – линии действия их пересекаются в центре Земли. Но, если пренебречь размерами тела в сравнении с размерами Земли, то можно считать их параллельными. (2)
(2) – вес каждой точки тела, а
– вес каждой точки тела, а  – вес всего тела.
– вес всего тела.
 можно отыскать точку с координатами
можно отыскать точку с координатами  . И координата
. И координата  по (2), будет равна нулю, т.к. в сумме
по (2), будет равна нулю, т.к. в сумме  все члены имеющие противоположные знаки, попарно уничтожаются. Значит центр тяжести расположен в плоскости симметрии.
все члены имеющие противоположные знаки, попарно уничтожаются. Значит центр тяжести расположен в плоскости симметрии. и координаты
и координаты  и
и  , вычисленные по формулам (2), окажутся равными нулю.
, вычисленные по формулам (2), окажутся равными нулю. , где
, где  - удельный вес материала, из которого сделано тело, а
- удельный вес материала, из которого сделано тело, а 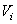 - объём этой части тела. И формулы (1) примут более удобный вид. Например,
- объём этой части тела. И формулы (1) примут более удобный вид. Например,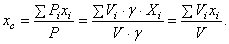

 где
где  - объём всего тела.
- объём всего тела. где
где 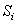 – площадь пластины, d – толщина. И координаты центра тяжести будут определяться только с помощью площадей:
– площадь пластины, d – толщина. И координаты центра тяжести будут определяться только с помощью площадей: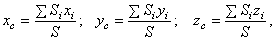
 – координаты центра тяжести отдельных пластин;
– координаты центра тяжести отдельных пластин;  – общая площадь тела.
– общая площадь тела.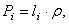 где li – длина,
где li – длина,  – вес единицы длины (погонного метра), а координаты центра тяжести будут определяться с помощью длин отдельных участков:
– вес единицы длины (погонного метра), а координаты центра тяжести будут определяться с помощью длин отдельных участков: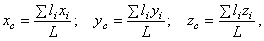
 – координаты центра тяжести
– координаты центра тяжести  -го участка;
-го участка; 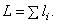


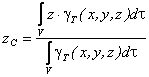
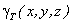 - вес единицы объема тела (удельный вес)
- вес единицы объема тела (удельный вес) - вес всего тела.
- вес всего тела.


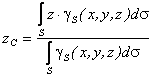
 - вес единицы площади тела,
- вес единицы площади тела, - вес всего тела.
- вес всего тела.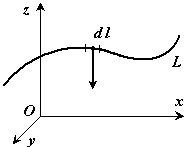


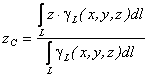
 - вес единицы длины тела ,
- вес единицы длины тела , - вес всего тела.
- вес всего тела.