|
|
Доказательства тождественности формулЛекция № 2. законы и тождества алгебры множеств
Продолжительность: 2 часа (90 мин.)
3.1 Ключевые вопросы · Основные законы и тождества алгебры множеств · Семейства множеств · Доказательства · Вопросы для контроля Текст лекции Основные законы и тождества алгебры множеств Основные законы алгебры множеств (булевой алгебры множеств) представляются в виде тождеств, в которых участвуют символы обозначений множеств, включая символы универсального и пустого множеств, и символы операций объединения, пересечения и дополнения. Ассоциативный закон 1) (X 2) (X Коммутативный закон 3) X Закон идемпотентности (повторения) 5) X Дистрибутивный закон 7) (X 8) (X Законы универсального U и пустого (законы нуля и единицы 9) X 11) X 13) Законы исключенного третьего и противоречия 15) X Законы де Моргана 17) Закон двойного отрицания 19) Если имеет место включение
Законы 5) и 6) можно записать и так X что позволяет при выполнении операций объединения и пересечения обходиться без коэффициентов и показателей степеней. При работе с множествами могут оказаться полезными тождества, приведенные ниже. Однако они требуют доказательства. Доказать их можно, используя основные законы (свойства операций пересечения, объединения и дополнения) и приемы, рассмотренные в п. 3.2.3 Дистрибутивный закон пересечения относительно разности
Дистрибутивный закон пересечения относительно симметрической разности
Дистрибутивный закон разности относительно пересечения
Дистрибутивный закон разности относительно объединения
Дистрибутивные законы объединения и пересечения относительно разности X\(Y X\(Y Представление пересечения и объединения через разность X X Законы нуля и единицы для разности (X \Y)
Законы поглощения
Закон склеивания
Свойства симметрической разности
Доказательства тождественности формул Наиболее часто в теории множеств возникает необходимость доказательства равенства соотношений типа Х = Y. Доказательство можно проводить путем рассуждений с применением законов и тождеств алгебры множеств, построением диаграмм Эйлера–Венна или на примерах конкретных множеств, составленных, например, из алфавитно–цифровых символов (последние два способа приведены в примере 2 п. 2.2.5 Лекции №1). Ниже, в примерах, доказательства соотношений типа X = Y, где Х и Y – множества, основаны на использовании определений I и II равенства двух множеств. В соответствии с определением I для равенства двух множеств требуется совпадение их элементов. Поэтому сначала доказывается, что для произвольного элемента а из того, что В соответствии с определением II Х = Y,если Пример 1.Доказать справедливость соотношения
Предположим, что произвольный элемент Следовательно, Пусть теперь некоторый элемент Следовательно, Таким образом, доказано, что Пример 2.Докажем по другому справедливость соотношения
Пусть имеем U ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {0, 1, 3, 7}, B = {2, 3, 4, 6, 7}. Определим левую часть:
= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}\{0, 1, 2, 3, 4, 6, 7} = {5, 8, 9}. Определим правую часть:
Как видим, левая часть равна правой, следовательно, соотношение справедливо. Замечание. Результаты операций при доказательстве тождеств не должны быть равными Пример 3.Доказать справедливость соотношения (A\B)\C = A\(B Используем соотношение Левая часть (A\B)\C = Правая часть A\(B Как видим, левая часть равна правой, следовательно, соотношение справедливо. Пример 4. Доказать справедливость соотношения
Это свойство дистрибутивности слева объединения Такое доказательство может быть выполнено с помощью диаграмм Эйлера–Венна (см. пример 2, п. 1.3). Здесь для этих целей используем один из приемов доказательства равенства двух множеств. В соответствии с первым определением равенства множеств множества равны, если их элементы совпадают. Это означает, что Х = Y, если из того, что 1. Покажем сначала, что если произвольный элемент а принадлежит левой части соотношения, т.е. Пусть Из определения операции объединения следует, что элемент а принадлежит объединению множеств А и 1.1. а принадлежит множеству А и а не принадлежит пересечению множеств
Последнее условие выполняется, если а не принадлежит В,или С, или им обоим (это является лишним); 1.2. 1.3. Рассмотрим каждый из этих случаев. 1.1. Так как
1.2. Так как 1.3. Так как Таким образом, в любом из рассмотренных случаев из того, что 2. Покажем теперь справедливость второго условия определения I равенства множеств: если произвольный элемент а не принадлежит левой части соотношения Пусть теперь: Элемент а не принадлежит объединению двух множеств, если он не принадлежит ни одному их них. Тогда 2.1. 2.2. 2.3. Рассмотрим каждый из этих случаев: 2.1. Так как
2.2. Так как
2.3. Так как Как видим, в любом из этих случаев из того, что Таким образом, множества
что и требовалось доказать. Пример 5.Доказать справедливость соотношения
Это свойство дистрибутивности справа пересечения Введем символ Множества Х = Y, если 1. Поэтому покажем сначала, что Пусть
Таким образом, 2. Покажем теперь, что Пусть
Следовательно, Таким образом, что и требовалось доказать. Семейства множеств Пусть дано множество U (конечное или бесконечное) и из элементов этого множества образована некоторая совокупность множеств Xa, называемая семейством множеств. Для семейства множеств справедливо
Если C = U, то имеем полное семейство. Если C = U и Над множествами, принадлежащими семействам, можно выполнять операции объединения и пересечения по обычным правилам. Символическая запись, например объединения совокупности множеств, имеет вид
а пересечение некоторого числа множеств обозначают так
В первом варианте объединяются или пересекаются множества, принадлежащие универсальному множеству U. Во втором варианте объединяются или пересекаютcя множества A1, A2, A3,…, An. В третьем варианте объединяется или пересекаетcя бесконечное число множеств A1, A2, A3,… В четвертом варианте объединяются или пересекаютcя множества, индекс которых принадлежит счетному множеству I (I = {1, 2, 3, …, n}). Для операций пересечения и объединения справедливо
Здесь Y – некоторое подмножество множества U. Пусть множества семейства формируются последовательным добавлением элементов. Если с некоторого k Хk+1 = Хk, то
Операция разности – бинарная, поэтому для семейств множеств она выполняется по следующим правилам
Прямое произведение семейства множеств X1, X2, …, Xn - это множество элементов вида ( Обозначается оно так
Как указывалось выше, элементы ( Произведение множеств – операция некоммутативная – переставлять множества в произведении нельзя. Если X1 = X2 = X3 =…= Xn = X, то Мощность множества | Для степени множества X получаем |X n| = |X|n. Для произведения множеств справедливы следующие свойства
Пусть дано семейство множеств А1, А2,…, Аn и пусть требуется определить мощность их объединения А1 В первом приближении можно принять за эту мощность сумму мощностей множеств семейства
однако, если пересечение, хотя бы для одной пары множеств, не пусто Аi то принадлежащие этому пересечению элементы будут учтены дважды. Исключение “лишних” элементов производится на основе принципа включений и исключений по формуле
Для трех множеств будем иметь
Вопросы для контроля 1. Какие “булевские” операции над множествами Вы знаете? Приведите примеры. 2. Какие операции, кроме “булевских”, применяют в теории множеств? 3. Поясните операцию перемножения множеств. Чему равна мощность произведения множеств? 4. Приведите основные законы “булевой” алгебры множеств. 5. Что такое булеан, как он строится и обозначается? Чему равна его мощность? Чему равно объединение и пересечение множеств, входящих в булеан? 6. Как выполняются операции объединения и пересечения над множествами А и В, если В является подмножеством А? 7. Что такое – семейство множеств? Как обозначаются операции объединения и пересечения множеств семейства? Каковы свойства этих операций? 8. На основе какого принципа (и как) производится определение мощности объединения множеств? Пересечения множеств? 9. Дайте определение равенству двух множеств. 10. Какие способы применяют для доказательства равенства двух выражений алгебры множеств? Приведите примеры. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
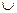 Y)
Y)  Y)
Y)  множеств
множеств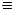 0, U
0, U  = U; 14)
= U; 14)  =
=  = U; 16) X
= U; 16) X  18)
18)  .
.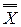 = X.
= X. (множество А является подмножеством множества В,см. рис. 1.1), то
(множество А является подмножеством множества В,см. рис. 1.1), то и
и  ,
, и
и  .
.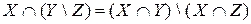 .
. .
.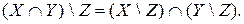
 .
. Z) = (X\Y)
Z) = (X\Y)  (X\Z);
(X\Z); ; X \
; X \  = X \U =
= X \U = 
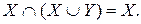
 .
. ,
, ,
,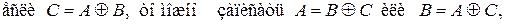
 ,
,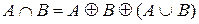 ,
, ,
, .
. , следует, что
, следует, что  , затем доказывается, что если
, затем доказывается, что если  ,то
,то  . Таким образом, элементы множеств X и Y совпадают и, следовательно, по определению I Х = Y.
. Таким образом, элементы множеств X и Y совпадают и, следовательно, по определению I Х = Y. и
и  . Поэтому для доказательства равенства двух множеств требуется показать справедливость включений
. Поэтому для доказательства равенства двух множеств требуется показать справедливость включений  и
и  .
. , т.е. что
, т.е. что  . Это значит, что
. Это значит, что  и
и 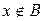 , значит
, значит  и
и 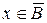 .
. .
. , т.е.
, т.е.  и
и  . Это значит, что
. Это значит, что  и
и  , т.е.
, т.е.  .
. .
. .
. = {0, 1, 3, 7}
= {0, 1, 3, 7}  = U\(
= U\(  = U\A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}\{0, 1, 3, 7} = {2, 4, 5, 6, 8, 9},
= U\A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}\{0, 1, 3, 7} = {2, 4, 5, 6, 8, 9}, = U\B ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}\{2, 3, 4, 6, 7} = {0, 1, 5, 8, 9},
= U\B ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}\{2, 3, 4, 6, 7} = {0, 1, 5, 8, 9}, = {2, 4, 5, 6, 8, 9}
= {2, 4, 5, 6, 8, 9}  .
.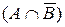 \С =
\С =  .
.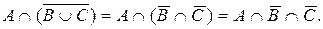
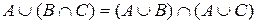 .
. , следует
, следует  .
.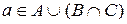 , то он принадлежит и правой части данного соотношения, т.е.
, то он принадлежит и правой части данного соотношения, т.е.  .
.  , если он принадлежит хотя бы одному из них (или, что очевидно, тому и другому). Таким образом,
, если он принадлежит хотя бы одному из них (или, что очевидно, тому и другому). Таким образом,  или
или  , при этом возможны следующие случаи:
, при этом возможны следующие случаи: :
: .
. и
и  ;
; .
. и
и  . Следовательно, а принадлежит и их пересечению:
. Следовательно, а принадлежит и их пересечению: ,
,  ,то
,то  , то он не принадлежит и правой части данного соотношения
, то он не принадлежит и правой части данного соотношения  .
. 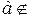 А и
А и  ,т.е. возможны следующие случаи:
,т.е. возможны следующие случаи: ;
; ;
; .
. , то
, то  , следовательно,
, следовательно, ,то
,то  ,следовательно,
,следовательно, и
и  совпадают и по определению равенства множеств
совпадают и по определению равенства множеств .
.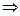 , который в выражениях типа Р
, который в выражениях типа Р  ,т.е. любой произвольный элемент а из множества, заданного левой частью соотношения, принадлежит и множеству, заданному правой частью соотношения.
,т.е. любой произвольный элемент а из множества, заданного левой частью соотношения, принадлежит и множеству, заданному правой частью соотношения. . Тогда
. Тогда или
или  .
. , т.е. любой элемент а из множества, заданного правой частью исходного соотношения, принадлежит и множеству, заданному левой частью исходного соотношения.
, т.е. любой элемент а из множества, заданного правой частью исходного соотношения, принадлежит и множеству, заданному левой частью исходного соотношения.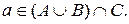

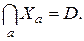
 , то совокупность множеств Xa образует систему классов эквивалентности (см. п. 3.6).
, то совокупность множеств Xa образует систему классов эквивалентности (см. п. 3.6).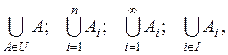
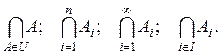
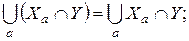
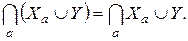
 .
.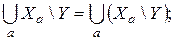
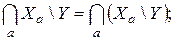
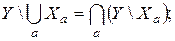
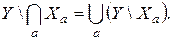
 ), где
), где 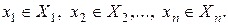
 или так
или так {(
{(  )|
)|  }.
}. ) называются кортежами, (векторами, наборами, словами). Количество множеств n, участвующих в произведении, определяет длину кортежей.
) называются кортежами, (векторами, наборами, словами). Количество множеств n, участвующих в произведении, определяет длину кортежей. .
. равна произведению мощностей множеств сомножителей
равна произведению мощностей множеств сомножителей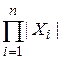 .
.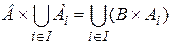 ,
, .
. .
. ,
, По этой формуле для двух множеств получаем
По этой формуле для двух множеств получаем