
|
|
Расчёт разветвлённых цепей методом проводимостей.И идеальным конденсатором.
Рассмотрим расчётную схему цепи с параллельно соединёнными резистором, идеальной катушкой и идеальным конденсатором (рис.4.9).
u = Um × sinwt. Определим мгновенное значение тока i . Запишем мгновенные значения токов в цепи в общем виде:
По первому закону Кирхгофа
Подставим мгновенные значения токов:
Построим векторную диаграмму напряжения и токов для случая, когда bl > bc (рис.4.10).
начальная фаза тока yi = –j . Очевидно, если bl < bc , то мгновенное значение тока
начальная фаза тока yi = j .
где b – реактивная проводимость цепи, См; угол сдвига фаз
активную проводимость
реактивную проводимость
Умножим стороны треугольника проводимостей на квадрат действующего значения напряжения и получим треугольник мощностей (рис.4.13). Мощности
Из треугольника токов (рис.4.11) и треугольника проводимостей (рис.4.12) следует, что расчётную схему, приведенную на рис.4.9, можно заменить эквивалентной со следующими обозначениями: iа , iр – соответственно активная и реактивная составляющие тока i , А; g , b – соответственно активная и реактивная проводимости цепи, См. Если bl > bc , то в цепи индуктивный режим и расчётная схема будет иметь вид, приведенный на рис.4.14. Если bl < bc , то в цепи емкостной режим и расчётная схема будет иметь вид, приведенный на рис.4.15.
Вопросы для самоконтроля 1. Как определить полную проводимость цепи с параллельным соединением 2. Составьте расчётную схему цепи с параллельным соединением 3. Составьте алгоритм расчёта токов в указанной выше цепи. 4. Что такое реактивная проводимость? Как её определить? 5. Что такое индуктивный режим работы указанной выше цепи? 6. Приведите расчётную схему указанной выше цепи для индуктивного режима работы. 7. Что такое емкостной режим работы указанной выше цепи? 8. Приведите расчётную схему указанной выше цепи для емкостного режима работы.
Эквивалентные расчётные схемы.
Рассмотрим расчётную схему цепи с последовательно соединенными активным и индуктивным сопротивлениями (рис.4.16). Построим треугольник сопротивлений этой цепи (рис.4.17).
Рассмотрим расчётную схему цепи, которая эквивалентна расчётной схеме, приведенной на рис.4.16, с параллельно соединенными активным и индуктивным сопротивлениями (рис.4.18). При эквивалентном преобразовании напряжение на зажимах цепи и ток в общей ветви не изменяются. Определим соотношения между параметрами приведенных схем. Построим треугольник проводимостей (рис.4.19).
Из треугольников сопротивлений и проводимостей находим:
Используя полученные соотношения, находим выражения для расчёта параметров эквивалентной схемы c параллельным соединением сопротивлений:
В свою очередь, эквивалентную схему с параллельным соединением сопротивлений можно заменить эквивалентной схемой с последовательным соединением сопротивлений, параметры которой определяются так:
Вопросы для самоконтроля 1. Перечислите условия эквивалентного преобразования электрической цепи. 2. Составьте расчётную схему цепи с последовательным соединением 3. Преобразуйте её в расчётную схему цепи с параллельным соединением 4. Запишите выражения для пересчёта параметров указанной выше цепи Расчёт разветвлённых цепей методом проводимостей.
Рассмотрим расчётную схему цепи (рис.4.20), в которой известны приложенное напряжение U и параметры r, x, r1, х1, r2, х2. Необходимо определить токи и
Алгоритм расчёта следующий: 1. Каждый участок цепи между точками 3 и 4 с последовательным соединением сопротивлений заменяем эквивалентной схемой с параллельным соединением сопротивлений (рис.4.21).
2. Определяем активную, реактивную и полную проводимости между точками 3 и 4: – проводимости первой ветви
– проводимости второй ветви
– активная проводимость между точками 3 и 4
– реактивная проводимость между точками 3 и 4
– полная проводимость между точками 3 и 4
3. Участок цепи между точками 3 и 4 полученной схемы с параллельным
4. Определяем полное, активное и реактивное сопротивления между точками – полное сопротивление между точками 3 и 4
– активное сопротивление между точками 3 и 4
– реактивное сопротивление между точками 3 и 4
6. Определяем полное, активное и реактивное сопротивления между точками – активное сопротивление между точками 1 и 2
– реактивное сопротивление между точками 1 и 2
– полное сопротивление между точками 1 и 2
7. Определяем ток и напряжение на участке 1–3:
8. Определяем напряжение и токи на участке 3–4:
9. Определяем углы сдвига фаз: – всей цепи
– первой ветви цепи
– второй ветви цепи
10. Определяем потребляемые мощности: – всей цепью
– первой ветвью цепи
– второй ветвью цепи
Вопросы для самоконтроля 1. Составьте расчётную схему цепи со смешанным соединением реальных катушек. 2. Составьте алгоритм анализа указанной выше цепи. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Пусть мгновенное значение
Пусть мгновенное значение 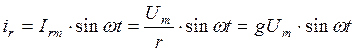 ;
; ;
; ;
; ,
, .
. .
. Как видно из векторной диаграммы, мгновенное значение тока
Как видно из векторной диаграммы, мгновенное значение тока ,
, ,
, Рассмотрим треугольник токов (рис.4.11). Силы токов могут быть определены так:
Рассмотрим треугольник токов (рис.4.11). Силы токов могут быть определены так: ;
; ;
; ;
; .
. Разделим стороны треугольника токов на максимальное значение напряжения и получим треугольник проводимостей (рис.4.12). Из него определим полную проводимость
Разделим стороны треугольника токов на максимальное значение напряжения и получим треугольник проводимостей (рис.4.12). Из него определим полную проводимость  ,
,
 ,
,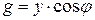 ,
, .
.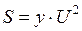 ;
;  ;
;  .
.


 ;
;  ;
;  .
. ;
;  .
. ;
;  .
.
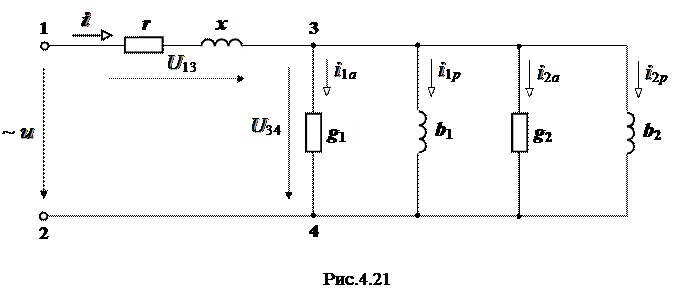
 ;
;  ;
;  ;
; ;
;  ;
;  ;
;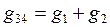 ;
; ;
; .
.
 ;
; ;
; .
. 5. Участок цепи между точками 1 и 2 полученной схемы с последовательным соединением сопротивлений заменяем эквивалентной схемой (рис.4.23).
5. Участок цепи между точками 1 и 2 полученной схемы с последовательным соединением сопротивлений заменяем эквивалентной схемой (рис.4.23). ;
;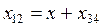 ;
; .
. ;
; 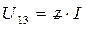 ;
;  .
. ;
; ;
;  ;
; ;
;  .
. ;
; ;
; .
. ;
;  ;
;  ;
; ;
;  ;
;  ;
; ;
;  ;
;  .
. 11. Строим векторную диаграмму, приняв yi = 0 и уменьшив в
11. Строим векторную диаграмму, приняв yi = 0 и уменьшив в  раз векторы токов и напряжений (рис.4.24).
раз векторы токов и напряжений (рис.4.24).