
|
|
Ручной счет Метод пр. итерации.12 Решение нелинейного уравнения Численные методы: Стадия определения корня: - Шаговый метод Стадия уточнения корня: - Метод половинного деления - Метод Ньютона - Метод пр. итерации Левая часть уравнения обозначается
Шаговый метод Цель: уменьшить промежуток [a;b] в n раз. Дано:
n – число разбиений Условие на сходимость: Условие на точность: нет Шаг
…
В ответ вписываем промежуток, где
Ручной счет. Шаговый метод. Численно решить нелинейное уравнение
Условие на сходимость:
…
…
Ответ: Метод половинного деления (итерационный мет) Цель: уточнить корень x Дано:
Условие на сходимость: Условие на точность: Итерационные формулы:


Ручной счет. Метод половинного деления. Численно решить нелинейное уравнение
Условие на сходимость:
Ответ: Метод Ньютона (итерационный метод) Цель: уточнить корень x Дано:
Условие на сходимость: Условие на точность: Итерационная формула:
Ручной счет. Метод Ньютона Численно решить нелинейное уравнение
Условие на сходимость: При
При
Ответ: Метод пр. итерации (итерационный метод) Цель: уточнить корень x Дано:
Условие на сходимость: Условие на точность: Итерационная формула: Ручной счет. Метод пр. итерации: Численно решить нелинейное уравнение
Выразим x:
Выразим x:
Ответ: Решение системы линейных уравнений Численные методы: - Метод Гаусса - Метод пр. итерации - Метод Зейделя Рассмотрим систему линейных уравнений с 4 неизвестными
Условия единственного решения: detA Система уравнений в матричной форме:
Метод Гаусса (точный метод) Цель: найти точное решение X системы линейных уравнений. Дано: Матрица А, В. Условия на сход: detA Условие на точность: нет М. Гаусса состоит из 2 этапов 1 этап – прямой ход: Привести матрицу А к
2 этап – обратный ход начиная с последнего уравнения и заканчивая первым выразить X4, X3, X2, X1 Ручной счет. Метод Гаусса. Численно решить систему линейных уравнений
Прямой ход:
  нужно получить «0» в первом столбце под главной диагональю нужно получить «0» в первом столбце под главной диагональю

~
 
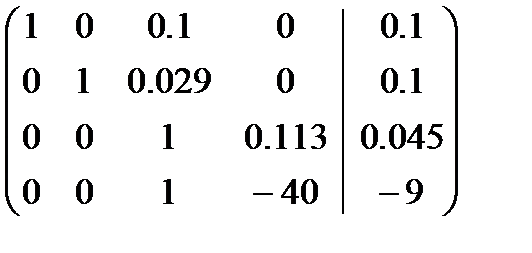 
~ ~ Обратный ход: 4 строчка: 3 строчка:
2 строчка:
1 строчка:
Ответ: Метод простой итерации (итерационный метод) Цель: найти решение Х систем линейных уравнений с точностью Ɛ Дано: матрицы А, В Точность Ɛ Условие на сход: detA В каждой строке модуль эл-та на главной диагонали> суммы модулей др. эл-тов.
Условие на точность: модуль разности нового и старого решений <
t Type="Embed" ProgID="Equation.3" ShapeID="_x0000_i1025" DrawAspect="Content" ObjectID="_1489657489"/></w:pict></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
Из уравнений выразить
Итерационные формулы:
Начальные приближения:
Ручной счет Метод пр. итерации. Численно решить систему линейных уравнений
С точностью Условие сход: detA
Итерационные формулы:
i=0 интер 1
I=1 интер.2
Ответ: 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 тогда уравнение в виде:
тогда уравнение в виде:  .
.
 - промежуток
- промежуток
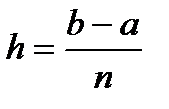









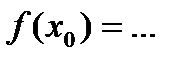
 на
на 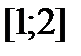 с числом разбиений 5.
с числом разбиений 5.


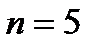


 - выполнено
- выполнено
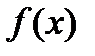



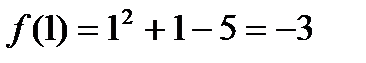

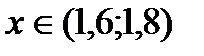
 - уравнение
- уравнение - промежуток
- промежуток - точность вычисления корня x
- точность вычисления корня x


 Если
Если  (корень слева)
(корень слева) Если
Если  (корень справа)
(корень справа)







 продолжаем вычисления
продолжаем вычисления

 ,
, 
 на промежутке
на промежутке 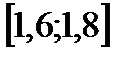 с точностью
с точностью  .
.
 ,
, 

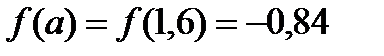

 - выполнено
- выполнено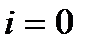
 ;
; 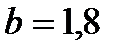


 - не выполнено
- не выполнено






 - не выполнено
- не выполнено






 - выполнено
- выполнено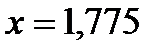 с точностью 0,1
с точностью 0,1 , где
, где  или b
или b



 >
>  - не выполнено
- не выполнено
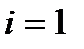


 на
на  с точностью
с точностью 




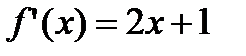




 не выполнено
не выполнено


 выполнено
выполнено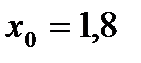

 - не выполнено
- не выполнено


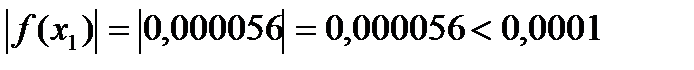 - выполнено
- выполнено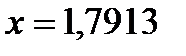 с точностью 0,0001
с точностью 0,0001





 - не выполнено
- не выполнено
 - не выполнено
- не выполнено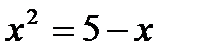




 - выполнено
- выполнено
 - выполнено
- выполнено


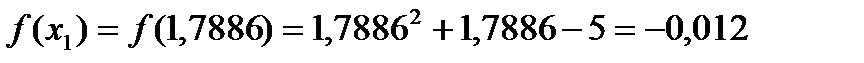
 - не выполнено
- не выполнено

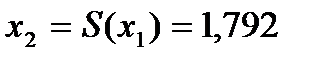

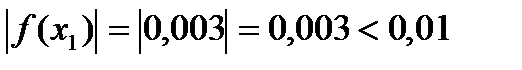 - выполнено
- выполнено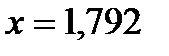 c точностью 0,01
c точностью 0,01
 ,
,  ,
,  ,
, 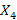 – неизветные:
– неизветные: 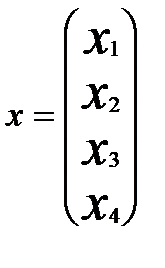
 - известные коэффициенты левых частей системы, которые входят в матрицу
- известные коэффициенты левых частей системы, которые входят в матрицу
 ,
,  ,
,  ,
,  – известные коэф-ты правых частей:
– известные коэф-ты правых частей: 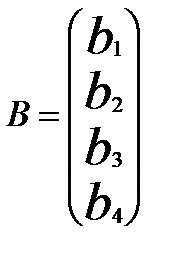
 0
0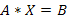
 виду:
виду:



 нужно получить «1» в первом столбце
нужно получить «1» в первом столбце
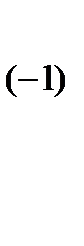









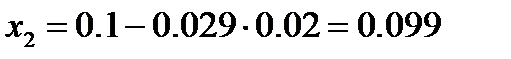
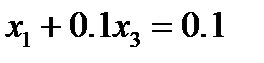


 - точное решение системы
- точное решение системы








 :
:  из (1),
из (1),  из (2) и тд.
из (2) и тд.




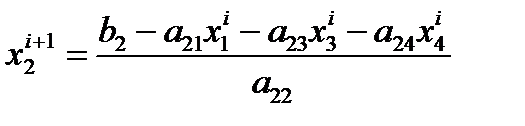




 =0,1.
=0,1. 10>1 – верно
10>1 – верно 7>2 – верно
7>2 – верно 9>6 – верно
9>6 – верно 4>1 – верно
4>1 – верно




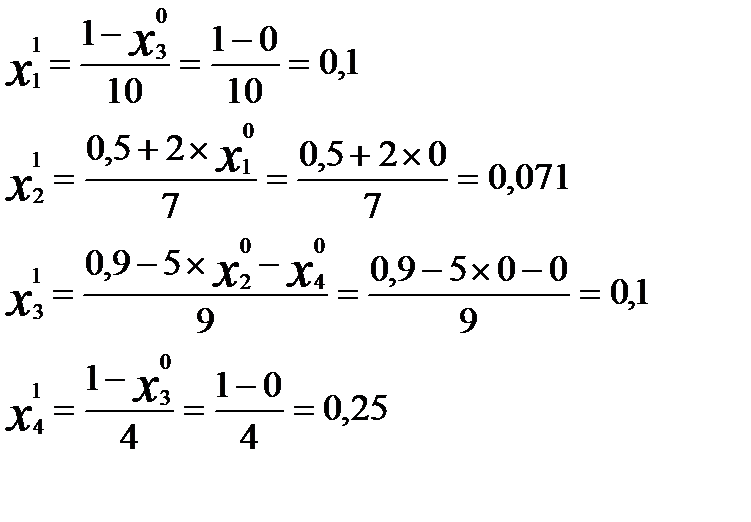


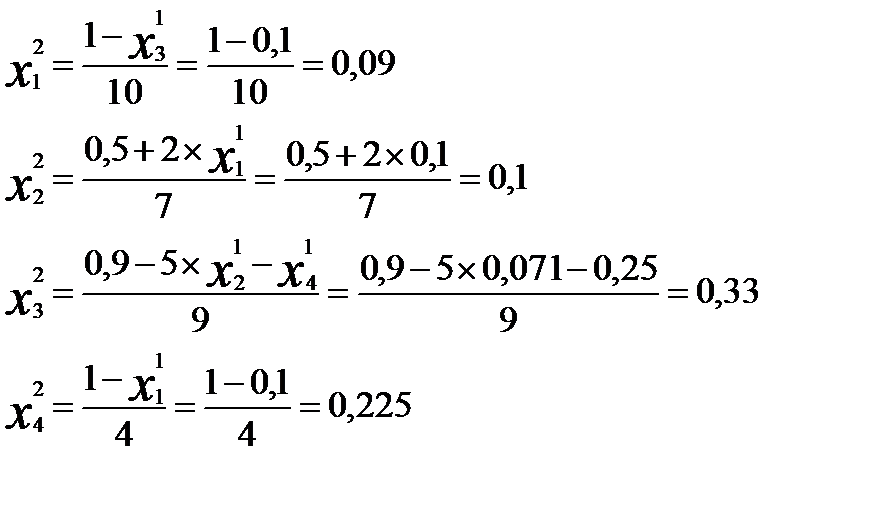

 - решение системы с точностью 0,1
- решение системы с точностью 0,1