
|
|
Первый множитель в (6) обращается в нуль в точках, для которыхГОУ ВПО Рыбинская государственная авиационная технологическая Академия им. П.А. Соловьева КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ
УТВЕРЖДЕНО на заседании методического семинара кафедры ОиТФ « » _________ 2007 г.
Зав.каф. Пиралишвили Ш.А.
Лаборатория «Волновая механика»
ЛАБОРАТОРНАЯ РАБОТА № ВМ – 5
ОПРЕДЕЛЕНИЕ ГРАНИЦ СПЕКТРА БЕЛОГО СВЕТА С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕШЕТКИ
Рыбинск 2007 ТРЕБОВАНЯИ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ Лабораторная установка имеет подключение к электрической сети напряжением 220 В и частотой 50 Гц. Требуется соблюдать нормы электробезопасности согласно инструкции №170. Специальные указания: гониометр Г-5 (прибор для измерения углов) выверен, требует аккуратного обращения. Приступать к исполнению работы можно только после ознакомления с инструкцией по технике безопасности и описанием прибора. Гониометр Г-5, на котором предстоит выполнить работу, точный оптический прибор, служащий для измерения углов с точностью до 1 секунды. Прибор настроен так, чтобы обеспечить успешное проведение измерений при минимальных затратах времени, поэтому не рекомендуется сбивать настройку прибора. Необходимо пользоваться только органами управления, помеченными цифрами.
ЦЕЛЬ РАБОТЫ: исследование дифракционного спектра, создаваемого дифракционной решеткой. ПРИБОРЫ И ОБОРУДОВАНИЕ: дифракционная решетка с периодом d = 0,01 мм, гониометр Г-5, осветитель, понижающий трансформатор. 1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Дифракция заключается в отклонении пучков волн от прямолинейного распространения и наблюдается практически при прохождении волн через отверстия в экранах или в пространстве экранирующих объектов, когда их размеры сравнимы с длиной волны. На объектах, значительно превышающих по своим размерам длину световой волны, дифракционная картина будет локализоваться очень далеко и может оказаться недоступной для наблюдения. Если, например, размеры экранирующего свет объекта составляют сотые доли миллиметра, то дифракционная картина может быть локализована в пределах небольшого лабораторного пространства, если же в качестве экранирующего объекта взять диск диаметром 10 см, то дифракционная картина локализуется на расстоянии порядка 1 км и для ее наблюдения необходимо создание специальных условий. На возможность геометрической интерпретации дифракции указывает принцип Гюйгенса. Пусть на непрозрачный экран с отверстием падает параллельный пучок света, которому соответствует плоский фронт волны (рис.1). Открытая часть, волнового фронта может рассматриваться как совокупность огромного числа виртуальных (от латинского virtual – возможный, вероятный) источников вторичных сферических элементарных волн. Согласно принципу Гюйгенса новый фронт волны – это огибающая всех элементарных фронтов волн. Дальнейшее направление распространения волны определится направлениями нормалей к волновому фронту. Из рис.1следует, что свет попадает в область геометрической тени. Однако, указывая на геометрическую возможность дифракции, принцип Гюйгенса не позволяет провести аналитическое исследование дифракционной картины. Анализ состояния светового поля за препятствием может быть выполнен на основе принципа Гюйгенса-Френеля, суть которого состоит в том, что световое колебание в точке пространства определяется как результат сложения колебаний от отдельных участков открытой части волнового фронта с учетом их фазы и амплитуды.
Дифракция плоских волн была впервые рассмотрена Фраунгофером. Пусть на бесконечно длинную щель падает плоская световая волна (рис2). Поместим за щелью собирающую линзу, а в фокальной плоскости линзы – экран. Волновая поверхность падающей волны, плоскость щели и экран параллельны друг другу. Поскольку щель бесконечна, картина, наблюдаемая в любой плоскости, перпендикулярной к щели, будет одинакова. Поэтому достаточно исследовать характер картины в одной такой плоскости, например в плоскости рис.2. Все вводимые в дальнейшем величины, в частности угол Разобьем открытую часть волновой поверхности на параллельные краям щели элементарные зоны ширины
где Обозначим алгебраическую сумму амплитуд колебаний, возбуждаемых в некоторой точке экрана всеми зонами, через
Отсюда
Теперь определим фазовые соотношения между колебаниями Таким образом, колебание, возбуждаемое элементарной зоной с координатой
(имеется в виду вещественная часть этого выражения). Проинтегрировав это выражение по всей ширине щели, найдем результирующее колебание, возбуждаемое в точке
Вынесем множители, не зависящие от
Выражение в фигурных скобках определяет комплексную амплитуду
Последнее выражение является вещественным. Его модуль представляет собой обычную амплитуду результирующего колебания:
Для точки, лежащей против центра линзы, При значениях
амплитуда Последнее условие легко получить из следующих соображений. Если разность хода Интенсивность света пропорциональна квадрату амплитуды, тогда из выражения (1) получаем
где Из последней формулы получается, что
Напротив, смещение линзы при неподвижной щели сопровождается таким же смещением картины на экране. График последней функции изображен на рис.4. По оси абсцисс отложены значения Количество минимумов интенсивности определяется отношением ширины щели При ширине щели, меньшей длины волны, минимумы вообще не возникают. В этом случае интенсивность света монотонно убывает от середины картины к ее краям. Краям центрального максимума соответствуют значения угла В случае, когда
Решим задачу о дифракции Фраунгофера от щели методом графического сложения амплитуд. Разобьем открытую часть волновой поверхности на очень узкие зоны одинаковой ширины. Колебание, возбуждаемое каждой такой зоной, имеет одинаковую амплитуду
Таким образом, центральный максимум значительно превосходит по интенсивности остальные максимумы; в нем сосредоточивается основная доля светового потока, проходящего через щель. В случае, когда ширина щели очень мала по сравнению с расстоянием от щели до экрана, лучи, идущие в точку Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей (рис. 6). Расстояние Расположим параллельно решетке собирающую линзу, в фокальной плоскости которой поставим экран. Выясним характер дифракционной картины, получающейся на экране при падении на решетку плоской световой волны (для простоты будем считать, что волна падает на решетку нормально). Каждая из щелей даст на экране картину, описываемую кривой, изображенной на рис. 4. Картины от всех щелей придутся на одно и то же место экрана (независимо от положения щели, центральный максимум лежит против центра линзы). Если бы колебания, приходящие в точку В дальнейшем мы будем предполагать, что радиус когерентности падающей волны намного превышает длину решетки, так что колебания от всех щелей можно считать когерентными друг относительно друга. В этом случае результирующее колебание в точке
(в данном случае роль
Из рис.6 видно, что разность хода от соседних щелей равна
где Подставив в формулу (4) выражение (3) для ( Первый множитель в (6) обращается в нуль в точках, для которых
В этих точках интенсивность, создаваемая каждой из щелей в отдельности, равна нулю (см. условие (2)). Второй множитель в (6) принимает значение
Для направлений, определяемых этим условием, колебания от отдельных щелей взаимно усиливают друг друга, вследствие чего амплитуда колебаний в соответствующей точке экрана равна
( Условие (8) определяет положения максимумов интенсивности, называемых главными. Число Возведя равенство (9) в квадрат, получим, что интенсивность главных максимумов Кроме минимумов, определяемых условием (7), в промежутках между соседними главными максимумами имеется
В формуле (10) Условие (10) легко получить методом графического сложения колебаний. Колебания от отдельных щелей изображаются векторами одинаковой длины. Согласно (10) каждый из последующих векторов повернут относительно предыдущего на один и тот же угол
Поэтому в тех случаях, когда Между дополнительными минимумами располагаются слабые вторичные максимумы. Число таких максимумов, приходящееся на промежуток между соседними главными максимумами, равно На рис. 8 приведен график функции (6) для
максимум Количество наблюдающихся главных максимумов определяется отношением периода решетки Определим угловую ширину центрального (нулевого) максимума. Положение ближайших к нему дополнительных минимумов определяется условием
Положение дополнительных минимумов, ближайших к главному максимуму
Обозначив
При большом числе щелей значение
При
Произведение В дифракционном спектре положение главных максимумов зависит от длины волны Основными характеристиками всякого спектрального прибора являются его дисперсия и разрешающая сила. Дисперсия определяет угловое или линейное расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу (например, на Угловой дисперсией называется величина
где Чтобы найти угловую дисперсию дифракционной решетки, продифференцируем условие (8) главного максимума слева по
Отсюда
В пределах небольших углов
– угловая дисперсия обратно пропорциональна периоду решетки Линейной дисперсией называют величину
Приняв во внимание выражение (11), получим для линейной дисперсии дифракционной решетки (при небольших
Разрешающей силой спектрального прибора называют безразмерную величину
где Возможность разрешения (т. е. раздельного восприятия) двух близких спектральных линий зависит не только от расстояний между ними (которое определяется дисперсией прибора), но также и от ширины спектрального максимума. На рис. 10 показана результирующая интенсивность (сплошные кривые), наблюдающаяся при наложении двух близких максимумов (пунктирные кривые). В случае а) оба максимума воспринимаются как один. В случае б) между максимумами лежит минимум. Два близких максимума воспринимаются глазом раздельно в том случае, если интенсивность в промежутке между ними составляет не более 80% от интенсивности максимума. Согласно критерию, предложенному Рэлеем, такое соотношение интенсивностей имеет место в том случае, если середина одного максимума совпадает с краем другого (рис. 10. б). Такое взаимное расположение максимумов получается при определенном (для данного прибора) значении Найдем разрешающую силу дифракционной решетки. Положение середины
Края
Середина максимума для длины волны
Решив это соотношение относительно Таким образом, разрешающая сила дифракционной решетки пропорциональна порядку спектра
2. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ Прибор гониометр Г-5 смонтирован на массивном металлическом основании. Его оптическая система (см. рис.11) состоит из коллиматора 1, обеспечивающего получение параллельного пучка света, зрительной трубы 2, и отсчетного микрометра 3 и ряда других узлов, смонтированных внутри корпуса прибора. Установка включает в себя также источник света – осветитель 4. На предметном столике 5, который может вращаться вокруг вертикальной оси, в специальном крепежном узле установлена дифракционная решетка с периодом Электрическая цепь прибора предполагает питание части узлов непосредственно от электрической сети, а части узлов – через понижающий трансформатор. Трансформатор имеет регулятор напряжения, позволяющий регулировать накал лампы осветителя. Желательно накал лампы устанавливать не предельный, а несколько ниже, чтобы не допускать перегрева корпуса. Питание измерительной оптической линии включается с помощью тумблера 10 на левой стороне корпуса прибора (внизу), а питание осветительного блока 4 с помощью тумблера 11 на корпусе трансформатора.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

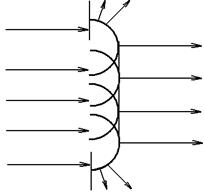 Рис. 1.
Рис. 1.
 Рис. 2.
Рис. 2.
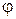 , образуемый лучом с оптической осью линзы, относятся к этой плоскости.
, образуемый лучом с оптической осью линзы, относятся к этой плоскости.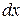 . Вторичные волны, посылаемые зонами в направлении, определяемом углом
. Вторичные волны, посылаемые зонами в направлении, определяемом углом  . Каждая элементарная зона создаст в точке
. Каждая элементарная зона создаст в точке 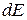 , где Е – напряженность электромагнитного поля световой волны. Амплитуда колебания, возбуждаемого зоной в любой точке экрана, будет зависеть только от площади зоны. Площадь пропорциональна ширине зоны
, где Е – напряженность электромагнитного поля световой волны. Амплитуда колебания, возбуждаемого зоной в любой точке экрана, будет зависеть только от площади зоны. Площадь пропорциональна ширине зоны 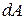 колебания
колебания 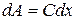 ,
,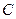 – константа.
– константа.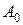 . Ее можно найти, проинтегрировав
. Ее можно найти, проинтегрировав 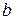 :
: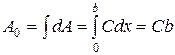 .
. , и, следовательно,
, и, следовательно,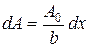 .
.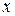 (рис. 2). Падающая волна –плоская, фронт ее отклоняется в результате дифракции на угол φ и занимает положение OQ после прохождения щели, где Q – основание перпендикуляра, опущенного из точки О.Оптические пути
(рис. 2). Падающая волна –плоская, фронт ее отклоняется в результате дифракции на угол φ и занимает положение OQ после прохождения щели, где Q – основание перпендикуляра, опущенного из точки О.Оптические пути 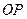 и
и 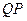 таутохронны (рис.2). Поэтому разность фаз между рассматриваемыми колебаниями образуется на пути
таутохронны (рис.2). Поэтому разность фаз между рассматриваемыми колебаниями образуется на пути 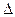 =
=  . Если начальную фазу колебания, возбуждаемого в точке
. Если начальную фазу колебания, возбуждаемого в точке  , положить равной нулю, то начальная фаза колебания, возбуждаемого зоной с координатой
, положить равной нулю, то начальная фаза колебания, возбуждаемого зоной с координатой 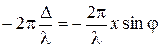 (
(  – длина волны в данной среде).
– длина волны в данной среде).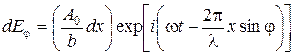
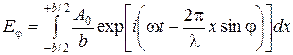 .
.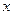 , за знак интеграла. Кроме того, введем обозначение
, за знак интеграла. Кроме того, введем обозначение 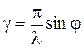 . В результате получим
. В результате получим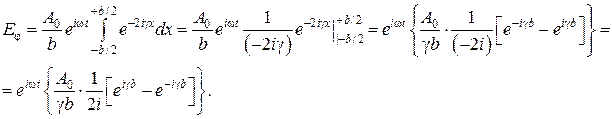
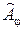 результирующего колебания. Приняв во внимание, что разность экспонент, деленная на
результирующего колебания. Приняв во внимание, что разность экспонент, деленная на 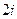 , представляет собой
, представляет собой 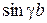 , можно написать
, можно написать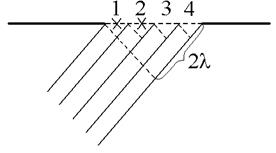 Рис. 3.
Рис. 3.
 .
.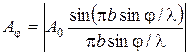 . (1)
. (1) . Подстановка этого значения в формулу (1) дает для амплитуды значение
. Подстановка этого значения в формулу (1) дает для амплитуды значение 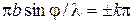 , т. е. в случае, если
, т. е. в случае, если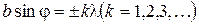 , (2)
, (2)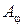 обращается в нуль. Таким образом, последнее условие определяет положения минимумов интенсивности. Отметим, что
обращается в нуль. Таким образом, последнее условие определяет положения минимумов интенсивности. Отметим, что 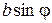 представляет собой разность хода
представляет собой разность хода  , открытую часть волновой поверхности можно разбить на
, открытую часть волновой поверхности можно разбить на  равных по ширине зон Френеля, причем разность хода от краев каждой зоны будет равна
равных по ширине зон Френеля, причем разность хода от краев каждой зоны будет равна  (см. рис. 3, выполненный для
(см. рис. 3, выполненный для  ). Колебания от каждой пары соседних зон взаимно погашают друг друга, так что результирующая амплитуда равна нулю. Если для точки
). Колебания от каждой пары соседних зон взаимно погашают друг друга, так что результирующая амплитуда равна нулю. Если для точки 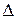 =
= 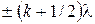 ,число зон будет нечетным, действие одной из них окажется некомпенсированным и наблюдается максимум интенсивности.
,число зон будет нечетным, действие одной из них окажется некомпенсированным и наблюдается максимум интенсивности.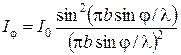 , (3)
, (3)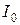 – интенсивность в середине дифракционной картины (против центра линзы),
– интенсивность в середине дифракционной картины (против центра линзы), 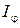 – интенсивность в точке, положение которой определяется данным значением
– интенсивность в точке, положение которой определяется данным значением 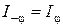 . Это означает, что дифракционная картина симметрична относительно центра линзы. Заметим, что при смещении щели параллельно экрану (вдоль оси
. Это означает, что дифракционная картина симметрична относительно центра линзы. Заметим, что при смещении щели параллельно экрану (вдоль оси  на рис. 2) дифракционная картина, наблюдаемая на экране, остается неподвижной (ее середина лежит против центра линзы).
на рис. 2) дифракционная картина, наблюдаемая на экране, остается неподвижной (ее середина лежит против центра линзы).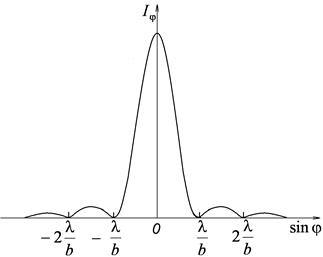 Рис. 4.
Рис. 4.
 , по оси ординат – интенсивность
, по оси ординат – интенсивность 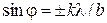 . Модуль
. Модуль 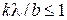 , откуда
, откуда 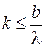 .
. . Эти значения равны
. Эти значения равны 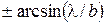 . Следовательно, угловая ширина центрального максимума равна
. Следовательно, угловая ширина центрального максимума равна  .
.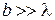 , значение
, значение  можно положить равным
можно положить равным 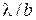 . Тогда формула для угловой ширины центрального максимума упрощается следующим образом:
. Тогда формула для угловой ширины центрального максимума упрощается следующим образом: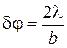 .
. и отстает по фазе от предыдущего колебания на одну и ту же величину
и отстает по фазе от предыдущего колебания на одну и ту же величину 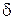 , зависящую от угла
, зависящую от угла 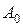 равна сумме амплитуд складываемых колебаний. Если
равна сумме амплитуд складываемых колебаний. Если  , колебания от краев щели находятся в противофазе. Соответственно векторы
, колебания от краев щели находятся в противофазе. Соответственно векторы  . В случае, когда
. В случае, когда 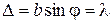 , колебания от краев щели отличаются по фазе на
, колебания от краев щели отличаются по фазе на 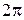 . Соответствующая векторная диаграмма изображена на рис. 5. в. Векторы
. Соответствующая векторная диаграмма изображена на рис. 5. в. Векторы 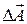 располагаются вдоль окружности длиной
располагаются вдоль окружности длиной 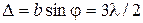 . В этом случае колебания от краев щели отличаются по фазе на
. В этом случае колебания от краев щели отличаются по фазе на 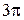 . Строя последовательно векторы
. Строя последовательно векторы 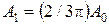 (рис. 5.г). Диаметр этой окружности и есть амплитуда первого максимума. Таким образом, интенсивность первого максимума равна
(рис. 5.г). Диаметр этой окружности и есть амплитуда первого максимума. Таким образом, интенсивность первого максимума равна 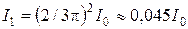 . Аналогично можно найти и относительную интенсивность остальных максимумов. В итоге получится следующее соотношение:
. Аналогично можно найти и относительную интенсивность остальных максимумов. В итоге получится следующее соотношение: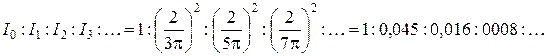 .
.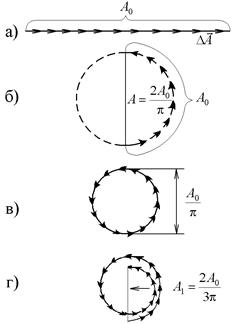 Рис. 5.
Рис. 5.
 между серединами соседних щелей называется периодом решетки.
между серединами соседних щелей называется периодом решетки.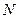 щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в
щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в 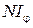 (
(  – интенсивность, создаваемая одной щелью).
– интенсивность, создаваемая одной щелью).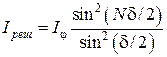 (4)
(4)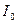 играет
играет 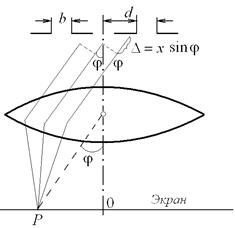 Рис. 6
Рис. 6
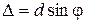 . Следовательно, разность фаз
. Следовательно, разность фаз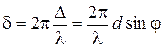 , (5)
, (5)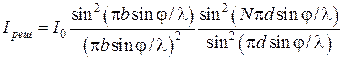 (6)
(6)
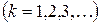 . (7)
. (7) в точках, удовлетворяющих условию
в точках, удовлетворяющих условию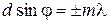 ,
,  . (8)
. (8)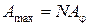 (9)
(9)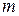 дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два.
дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два. в
в  раз больше интенсивности
раз больше интенсивности 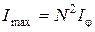 .
. добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием
добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием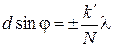 , (10)
, (10)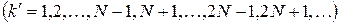 .
. Рис. 7
Рис. 7
 принимает все целочисленные значения, кроме
принимает все целочисленные значения, кроме 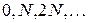 , т. е. кроме тех, при которых условие (10) переходит в (8).
, т. е. кроме тех, при которых условие (10) переходит в (8).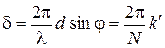 .
.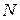 , мы, пристраивая начало следующего вектора к концу предыдущего, получим замкнутую ломаную линию, которая делает
, мы, пристраивая начало следующего вектора к концу предыдущего, получим замкнутую ломаную линию, которая делает 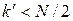 ) или
) или 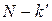 (при
(при 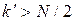 ) оборотов прежде, чем конец
) оборотов прежде, чем конец  и значений
и значений 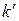 , равных
, равных 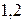 и
и  .
. 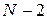 . Ранее было показано, что интенсивность вторичных максимумов не превышает
. Ранее было показано, что интенсивность вторичных максимумов не превышает  интенсивности ближайшего главного максимума.
интенсивности ближайшего главного максимума.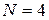 и
и 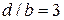 . Пунктирная кривая, проходящая через вершины главных максимумов, изображает интенсивность от одной щели, умноженную на
. Пунктирная кривая, проходящая через вершины главных максимумов, изображает интенсивность от одной щели, умноженную на 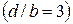 главные максимумы 3-го, 6-го и т. д. порядков приходятся на минимумы интенсивности от одной щели, вследствие чего эти максимумы пропадают. Вообще из формул (7) и (8) вытекает, что главный максимум
главные максимумы 3-го, 6-го и т. д. порядков приходятся на минимумы интенсивности от одной щели, вследствие чего эти максимумы пропадают. Вообще из формул (7) и (8) вытекает, что главный максимум  -й минимум от одной щели, если будет выполнено равенство:
-й минимум от одной щели, если будет выполнено равенство: 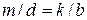 , или
, или 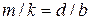 . Это возможно, если
. Это возможно, если 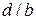 равно отношению двух целых чисел
равно отношению двух целых чисел 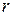 и
и 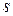 (практический интерес представляет случай, когда эти числа невелики). Тогда главный
(практический интерес представляет случай, когда эти числа невелики). Тогда главный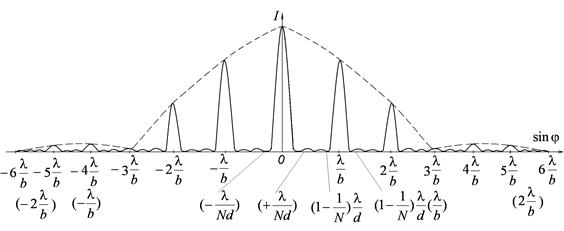 Рис. 8
Рис. 8
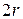 -го порядка - на
-го порядка - на 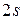 -й минимум и т. д., в результате чего максимумы порядков
-й минимум и т. д., в результате чего максимумы порядков 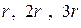 и т. д. будут отсутствовать.
и т. д. будут отсутствовать.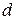 к длине волны
к длине волны  .
. (см. формулу (10)), этим минимумам соответствуют
(см. формулу (10)), этим минимумам соответствуют 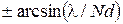 , где
, где 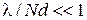 ,
,  .
.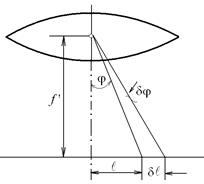 Рис. 9
Рис. 9
 . Отсюда получается для угловой ширины
. Отсюда получается для угловой ширины 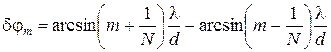 .
.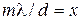 и
и 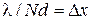 , имеем
, имеем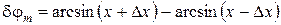 .
. будет очень мало, потому
будет очень мало, потому  , и
, и .
.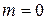
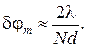
 Рис. 10
Рис. 10
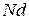 дает длину дифракционной решетки. Следовательно, угловая ширина главных максимумов обратно пропорциональна длине решетки. С увеличением порядка максимума
дает длину дифракционной решетки. Следовательно, угловая ширина главных максимумов обратно пропорциональна длине решетки. С увеличением порядка максимума 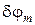 возрастает.
возрастает.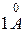 ). Разрешающая сила определяет минимальную разность длин волн
). Разрешающая сила определяет минимальную разность длин волн 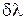 , при которой две линии воспринимаются в спектре раздельно.
, при которой две линии воспринимаются в спектре раздельно.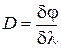 ,
,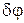 – угловое расстояние между спектральными линиями, отличающимися по длине волны на
– угловое расстояние между спектральными линиями, отличающимися по длине волны на 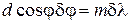 .
.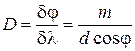 .
.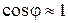 , поэтому можно положить
, поэтому можно положить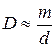 (11)
(11) , где
, где 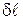 – линейное расстояние на экране или на фотопластинке между спектральными линиями, отличающимися по длине волны на
– линейное расстояние на экране или на фотопластинке между спектральными линиями, отличающимися по длине волны на 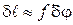 , где
, где 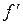 – фокусное расстояние линзы, собирающей дифрагирующие лучи на экране. Следовательно, линейная дисперсия связана с угловой дисперсией
– фокусное расстояние линзы, собирающей дифрагирующие лучи на экране. Следовательно, линейная дисперсия связана с угловой дисперсией 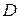 соотношением
соотношением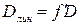 .
.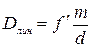 .
.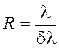 ,
, определяется условием
определяется условием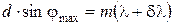 .
.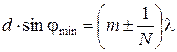 .
.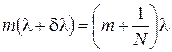 . Отсюда
. Отсюда .
.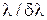 , получим выражение для разрешающей силы
, получим выражение для разрешающей силы 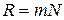 .
.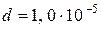 м. Решетка установлена перпендикулярно световому потоку, выходящему из коллиматора. Фиксация установки дифракционной решетки производится с помощью винтов 6 и 7, эта операция выполняется лаборантом при подготовке прибора к работе. Непосредственно под предметным столиком расположен крупногабаритный узел 8, называемый алидадой. Внутри ее корпуса находится отсчетный лимб (круглая шкала). Показания прибора снимаются с помощью отсчетного микрометра 3.
м. Решетка установлена перпендикулярно световому потоку, выходящему из коллиматора. Фиксация установки дифракционной решетки производится с помощью винтов 6 и 7, эта операция выполняется лаборантом при подготовке прибора к работе. Непосредственно под предметным столиком расположен крупногабаритный узел 8, называемый алидадой. Внутри ее корпуса находится отсчетный лимб (круглая шкала). Показания прибора снимаются с помощью отсчетного микрометра 3.