
|
|
Правила дифференцирования.Реферат Тема«Вторая производная, ее геометрический и физический смысл».
Работу выполнила студентка 22группы Синильникова Анастасия г.Бологое Введение. Определение:Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение Стандартные обозначения второй производной: Геометрический смысл второй производной. Вторая производная f" (x) имеет также важное значение в анализе и в геометрии; в самом деле, представляя собой скорость изменения наклона f (х) кривой y = f (x), вторая производная дает указание на то, как изогнута кривая. Если в некотором промежутке вторая производная больше нуля, то скорость изменения наклона f' (х) положительна. Положительный знак скорости изменения некоторой функции указывает на то, что эта функция возрастает с возрастанием аргумента х. Следовательно, неравенство f" (х) > 0 указывает на то, что наклон f (x) есть возрастающая функция х и, значит, при увеличении х кривая становится более крутой там, где наклон ее положителен, и более пологой там, где наклон отрицателен. Условимся говорить, что в этом случае кривая вогнута (рис. 1). Аналогично если f" (х) <0, то будем говорить, что кривая y = f (х) (х) выпукла (рис. 2)
Рис. 1-2. Вогнутость и выпуклость кривой Парабола y = f (х) = х2 всюду вогнута, так как ее вторая производная (f" (х) = 2) всегда положительна. Кривая y = f (х) = x3 вогнута при х>0 и выпукла при х<0; это видно по ее второй производной f" (х) = 6х, в чем читатель может легко убедиться сам. Между прочим, при х = 0 имеем f' (х) = 3х 2 = 0 (но нет ни минимума, ни максимума!), а также и f" (х) = 0 при х = 0. Эта точка называется тезкой перегиба. В точках, которые так называются, касательная (в данном случае ось х) пересекает кривую. Если буква s обозначает длину дуги кривой, а буква α - угол наклона, то функция α = h (s) есть функция переменного s. При передвижении точки по кривой функция α = h (s) будет меняться. Скорость этого изменения h' (s) принято называть кривизной кривой в точке, для которой длина дуги равна s. Без доказательства отметим, что кривизна k может быть выражена с помощью первой и второй производных от функции y = f (x),определяющей кривую, согласно следующей формуле: k = f"(x):(1 + (f'(x))2)3/2 Физический смысл второй производной. Если Пример 17. Как известно, уравнение движения свободно падающего в безвоздушном пространстве тела, начавшего свое падение в момент То есть ускорение A падающего тела неизменно и равно G – ускорению свободного падения ( Дифференциал функции. Вернемся к записи Эта простенькая формула содержит в себе великий смысл («все великое просто»). В ней содержится даже некоторое мистическое свойство. Расшифруем Находясь в сегодня Y(X0) и зная На языке математики это означает: не зная самой функции F(X) и таким образом, не имея возможности ее изучать, можно только с помощью двух чисел Применение этой формулы способствовало решению многих физических, практических задач из различных сфер деятельности человека. Произведение Дифференциал есть бесконечно малая величина. Но эта величина содержит в себе огромную информацию о функции. Точно так же капля крови под микроскопом говорит знающему человеку очень много о его здоровье. Для вычисления дифференциала надо знать производную, именно поэтому процедура нахождения производной от функции называется дифференцированием. Правила дифференцирования. 1. Производная от постоянной равна нулю: 2. Постоянную величину можно вынести за знак производной: Пусть U(X) и V(X) дифференцируемые функции, тогда: 3. Производная от алгебраической суммы двух функций равна алгебраической сумме производных: Добавляя третье слагаемое, далее четвертое и т. д. можно получить правило по которому надо последовательно дифференцировать все слагаемые, оставляя между ними знаки «+» или «–», как они и стояли. 4. Производная от произведения превращается в сумму двух произведений: Можно добавить третий множитель, тогда: 5. Производная частного: Таблица производных. Это значения производных от элементарных функций. Такие таблицы имеются в любом справочнике по высшей математике. Покажем только на одном примере, как выводятся табличные производные. Пусть
В практической жизни чаще всего приходится иметь дело со сложными функциями, например,

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
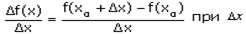 , стремящемуся к нулю.
, стремящемуся к нулю. ,
, 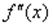 или
или 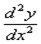 (дробь читается так: «дэ два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите
(дробь читается так: «дэ два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите  функции…».
функции…». 
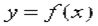 – уравнение движения точки по ее траектории. рис., то, как мы знаем, ее производная
– уравнение движения точки по ее траектории. рис., то, как мы знаем, ее производная  (производная первого порядка) представляет собой скорость V(X) движения точки (мгновенную скорость движения), но тогда производная второго порядка
(производная первого порядка) представляет собой скорость V(X) движения точки (мгновенную скорость движения), но тогда производная второго порядка 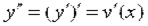 будет иметь смысл «скорость изменения скорости» движения точки. В физике такая величина называется ускорением. Поэтому – ускорение движения точки в момент X. В этом и состоит физический смысл производной второго порядка.
будет иметь смысл «скорость изменения скорости» движения точки. В физике такая величина называется ускорением. Поэтому – ускорение движения точки в момент X. В этом и состоит физический смысл производной второго порядка.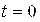 , имеет вид:
, имеет вид:  (S – путь, пройденный падающим телом за время T). Найдем скорость
(S – путь, пройденный падающим телом за время T). Найдем скорость 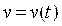 и ускорение
и ускорение  падающего тела:
падающего тела: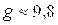 м/сек2). А скорость V падающего тела возрастает пропорционально времени по формуле
м/сек2). А скорость V падающего тела возрастает пропорционально времени по формуле 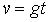 .
.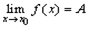 . Это значит, что в окрестности
. Это значит, что в окрестности 
 , где
, где 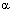 – бесконечно малая. Рассмотрим запись
– бесконечно малая. Рассмотрим запись  . Она означает, что
. Она означает, что 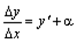 . Отбрасывая
. Отбрасывая  получим:
получим: 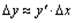
 и перепишем Получим:
и перепишем Получим:  .
. тоже сегодня, можно предсказать, что будет с нами завтра Y(X0 + DX).
тоже сегодня, можно предсказать, что будет с нами завтра Y(X0 + DX). и
и  и с помощью вычислить значения функции в другой точке, близкой к X0.
и с помощью вычислить значения функции в другой точке, близкой к X0. получило название дифференциала функции, правда, пришлось заменить DX на Dx (дифференциал X), имея в виду его бесконечную малость. Итак, Def:
получило название дифференциала функции, правда, пришлось заменить DX на Dx (дифференциал X), имея в виду его бесконечную малость. Итак, Def:  .
. .
. .
.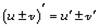 .
.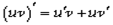 .
.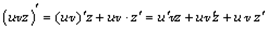 .
. .
. ,
, 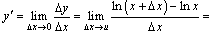 │разность логарифмов равна логарифму частного │
│разность логарифмов равна логарифму частного │ 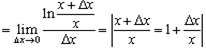 =
=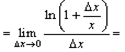 │воспользуемся эквивалентность
│воспользуемся эквивалентность 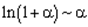 , если
, если 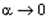 , т. е.
, т. е.  при
при  │
│  .
. , где
, где  ;
;  , где
, где  и т. д. Поэтому таблицу производных для элементарных функций мы записываем, учитывая их сложность.
и т. д. Поэтому таблицу производных для элементарных функций мы записываем, учитывая их сложность.