
|
|
Предельные производительность, спрос, предложенияЭкономический смысл выпуклости функции
Закон убывающей доходности: с увеличением производства дополнительная продукция, полученная на каждую новую единицу ресурса (трудового, технологического и т.д.), с некоторого момента убывает. Иными словами, величина Закон убывающей полезности: с ростом количества товара дополнительная полезность от каждой новой его единицы с некоторого момента убывает. Функция полезности
Задания для самостоятельной работы
1. Найдите предельную производительность ресурса (скорость изменения функции), если функция выпуска имеет вид:
а затраты ресурса составляют: 1) 2 усл.ед., 2) 5 усл.ед. Определите, начиная с какого момента увеличение затрат данного ресурса становится экономически невыгодным. Приведите примеры экономических ситуаций, которые могут быть описаны с помощью функций выпуска указанного вида. 2. Определите скорость изменения спроса (предельный спрос) при цене в 1 ден.ед.; 3 ден.ед.; 10 ден.ед., если зависимость спроса на товар от цены на него выражается формулой
Сравните и объясните результаты. Лекция 3. Исследование функций в экономике. Предельные производительность, спрос, предложения
На основании экономического смысла производной и аппарата дифференциального исчисления возникает множество экономических задач, связанных с исследованием функций. В частности, представляют интерес экономические понятия и задачи на предельную производительность ресурса, предельный спрос продукции от цены и т.д. Приведем определение и примеры таких задач. Пример 10. Предприятие производит
1.
2.
Вывод: финансовые накопления предприятия растут с увеличением объема производства до 100 единиц, при Пример 11. Цементный завод производит
Удельные затраты это средние затраты на единицу продукции, в данном случае на 1 т цемента. При объеме производства в
Задача сводится к отысканию наибольшего, наименьшего значения функции
на промежутке Ответ: Указание. Обозначим ширину прямоугольного участка через х, а длину через у. Из условий задачи следует, что х ).¥ (0, Î Поскольку площадь участка равна 294 кв. м., то х × у=S=294. Откуда получаем, что у=294/х, а общая длина ^ Р всего загона равна: Р(х)=3х 2у=3х 2 ´ 294/х Таким образом, общая длина ограды представляет собой функцию от одной переменной х).¥, и наша задача свелась к нахождению наименьшего значения этой функции в интервале (0, Ответ: Пусть в производстве продукции используется несколько видов сырья. Однако затраты всех ресурсов строго регламентированы технологией производства. Только один ресурс (например, затраты труда) может изменяться, оказывая влияние на объем производства. Зависимость выпуска продукции
Скорость изменения этой функции выражается ее производной и называется предельной производительностью ресурса. Если речь идет о затратах труда, то
Естественно, возникает вопрос: какова скорость изменения
Скорость изменения предельной производительности ресурса называется темпом изменения выпуска при изменении затрат этого ресурса. Пример 13. Если формула
выражает зависимость спроса на товар от цены на него, то
- скорость изменения спроса, или предельный спрос. Спрос является убывающей функцией цены, т.к.
Другими словами, спрос убывает с нарастающей скоростью. Чем больше цена, тем быстрее уменьшается спрос на товар. Если Определение. Монотонная функция Очевидна, справедлива следующая Теорема. Для того, чтобы функция Пример 14. Предположим, что на предприятии издержки производства вычисляются по формуле
Предельные издержки
положительны при любом объеме производства Вычислим Введем следующие обозначения:
Предположим, что масса основных фондов пропорциональна объему производства:
где
Это означает, что прирост основных производственных фондов в единицу времени пропорционален приросту выпуска предметов потребления в единицу времени. Прирост основных фондов в единицу времени есть результат капиталовложений
т.е. капиталовложения пропорциональны приросту объема производства. Пример 15. Объем производства предметов потребления в период времени
Для Из (3) и условия Поведение графиков функций
1. Если спрос на предметы потребления (или, что то же самое, на производство) возрастает в каком-либо периоде все быстрее (промежуток 2. Если спрос на предметы потребления (или их производство) с какого-то момента начинает расти все медленнее (промежуток 3. Удержание капиталовложений на уровне, достигнутом в момент времени Приведенное положение называют принципом ускоренияили принципом акселератора. Пример 16. Зависимость спроса от цены описывается функцией
Исследовать функции спроса и выручки от цены, построить их графики. Спрос убывает с возрастанием цены, так как
Темп изменения функции
Выручка от реализации товара по цене
Производная этой функции
положительна, если
Дальнейшее увеличение цены не имеет смысла, так как оно ведет к сокращению выручки. Темп изменения выручки
положительный, если На промежутке Для неограниченном увеличении цены. На промежутке
Найдите предельную выручку и постройте ее график. Пользуясь этим графиком, определите, при каком объеме производства выручка максимальна (минимальна). Чему равна при этом предельная выручка? Что это означает? Замечание. Предельная выручка определяется аналогично предельным издержкам производства (это скорость изменения выручки при данном объеме продаж). 2. Предприятие производит
Суммарные издержки производства составляют:
Определите, при каком объеме производства прибыль предприятия будет максимальной. 3. Из треугольных обрезков фанеры необходимо сделать заготовки, имеющие форму параллелограмма. Как добиться того, чтобы заготовки имели максимально возможную площадь? 4. Имеется запас меда стоимостью в Определите момент времени 5. Зависимость полных издержек производства
Рассчитайте, при каком объеме производства средние издержки минимальны ( 6. Цена бриллианта пропорциональна квадрату его массы. Если бриллиант разбить на две части. То в каком случае общая стоимость двух частей будет наименьшей? 7. Предположим, что функция затрат имеет вид:
Определите предельные издержки производства при объеме выпуска 8. Установлено, что предложение данного товара описывается формулой 9. Функция спроса на товар имеет вид:
Определите уровни цен, соответствующих максимальному спросу на товар, исчезновению спроса на него. При какой цене предельный спрос (скорость изменения спроса) будет равен нулю, двум, десяти? Чему равен темп изменения спроса? Что это означает? Приведите примеры ситуаций, которые могут быть описаны с помощью функций указанного вида.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где
, где  - приращение ресурса, а
- приращение ресурса, а  - приращение выпуска продукции, уменьшается при увеличении
- приращение выпуска продукции, уменьшается при увеличении  . Таким образом, закон убывающей доходности формулируется так: функция
. Таким образом, закон убывающей доходности формулируется так: функция  , выражающая зависимость выпуска продукции от вложенного ресурса, является функцией выпуклой вверх.
, выражающая зависимость выпуска продукции от вложенного ресурса, является функцией выпуклой вверх. , где
, где 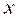 - товар,
- товар,  - полезность, есть величина субъективная для каждого отдельного потребителя, но достаточно объективная для общества в целом. Очевидно, закон убывающей полезности можно переформулировать так: функция полезности является функцией выпуклой вверх.
- полезность, есть величина субъективная для каждого отдельного потребителя, но достаточно объективная для общества в целом. Очевидно, закон убывающей полезности можно переформулировать так: функция полезности является функцией выпуклой вверх. ,
, .
. .
. .
. .
. 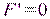 при
при  и
и  . На промежутке
. На промежутке  производная положительна, на
производная положительна, на  - отрицательна. В точке
- отрицательна. В точке  функция достигает максимума:
функция достигает максимума: .
. они достигают максимума, равного 39000 ден.ед., дальнейший рост производства приводит к сокращению финансовых накоплений.
они достигают максимума, равного 39000 ден.ед., дальнейший рост производства приводит к сокращению финансовых накоплений. тонн цемента в день. По договору он должен ежедневно поставлять строительной фирме не менее 20 т цемента. Производительные мощности завода таковы. Что выпуск цемента не может превышать 90 т в день. Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид:
тонн цемента в день. По договору он должен ежедневно поставлять строительной фирме не менее 20 т цемента. Производительные мощности завода таковы. Что выпуск цемента не может превышать 90 т в день. Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид: .
. т удельные затраты составят:
т удельные затраты составят: .
.
 .
.
 .
. от затрат этого специфического ресурса
от затрат этого специфического ресурса  описывается формулой
описывается формулой .
. - предельная производительность труда. Значение
- предельная производительность труда. Значение  , т.е. речь идет о новой функции аргумента
, т.е. речь идет о новой функции аргумента  , а именно о
, а именно о .
. ? Скорость изменения любой функции описывается ее производной. Если функция
? Скорость изменения любой функции описывается ее производной. Если функция  дифференцируема, то существует
дифференцируема, то существует .
.

 при любом значении
при любом значении  . Темп изменения спроса
. Темп изменения спроса .
. , то
, то  .
. возрастает (убывает) на
возрастает (убывает) на  все быстрее, если скорость ее изменения является возрастающей функцией. Если же скорость изменения функции
все быстрее, если скорость ее изменения является возрастающей функцией. Если же скорость изменения функции  , то говорят, что функция
, то говорят, что функция  возрастает (убывает) на
возрастает (убывает) на  , имеющая на промежутке
, имеющая на промежутке  первую и вторую производные, возрастала (убывала) на нем все быстрее, необходимо и достаточно, чтобы выполнялись условия
первую и вторую производные, возрастала (убывала) на нем все быстрее, необходимо и достаточно, чтобы выполнялись условия  для всех
для всех  .
. .
.
 . Это следует из того, что дискриминант квадратного трехчлена
. Это следует из того, что дискриминант квадратного трехчлена  отрицателен, а старший коэффициент 1 положителен. Такой трехчлен может принимать только положительные значения.
отрицателен, а старший коэффициент 1 положителен. Такой трехчлен может принимать только положительные значения. . Легко установить, что
. Легко установить, что 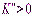 , если
, если  , и
, и  при
при  . Следовательно, если выпуск продукции не превышает 5усл.ед., то издержки производства возрастают все медленнее. Если же
. Следовательно, если выпуск продукции не превышает 5усл.ед., то издержки производства возрастают все медленнее. Если же  , то издержки растут все быстрее.
, то издержки растут все быстрее. - размеры основных производственных фондов в момент времени
- размеры основных производственных фондов в момент времени  ,
, - объем производства предметов потребления с помощью основных производственных фондов
- объем производства предметов потребления с помощью основных производственных фондов  .
. ,
, - постоянный коэффициент пропорциональности (
- постоянный коэффициент пропорциональности (  ). Следовательно,
). Следовательно, .
. . Можно, следовательно, записать, что в момент времени
. Можно, следовательно, записать, что в момент времени 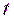
 ,
, возрастает все быстрее, а с момента
возрастает все быстрее, а с момента  до
до  возрастает все медленнее. Дать характеристику зависимости капиталовложений от спроса на предметы потребления.
возрастает все медленнее. Дать характеристику зависимости капиталовложений от спроса на предметы потребления. , а для
, а для  . Это означает, что функция
. Это означает, что функция 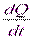 возрастает в промежутке
возрастает в промежутке  и убывает для
и убывает для  .
. следует, что
следует, что  имеет такой же характер изменения, что и
имеет такой же характер изменения, что и  . Поэтому функцию
. Поэтому функцию  можно изобразить кривой, приведенной на рисунке 7.
можно изобразить кривой, приведенной на рисунке 7. позволяет сделать следующие выводы.
позволяет сделать следующие выводы.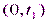 ), то возрастают и капиталовложения. Следовательно, растет спрос на предметы производства, необходимые для увеличения выпуска предметов потребления.
), то возрастают и капиталовложения. Следовательно, растет спрос на предметы производства, необходимые для увеличения выпуска предметов потребления. ), это вызовет уменьшение размеров капиталовложений, т.е. падение спроса на средства производства.
), это вызовет уменьшение размеров капиталовложений, т.е. падение спроса на средства производства. , возможно лишь в случае, если спрос на предметы потребления возрастает постоянным темпом, достигнутым в момент времени
, возможно лишь в случае, если спрос на предметы потребления возрастает постоянным темпом, достигнутым в момент времени  .
. .
. отрицателен, если
отрицателен, если  , и положителен, когда цена больше
, и положителен, когда цена больше  . График изображен на рис.8.
. График изображен на рис.8. составляет:
составляет: ден.ед.
ден.ед.
 , и отрицательна для
, и отрицательна для  . Это означает, что с ростом цены выручка вначале увеличивается (несмотря на падение спроса) и при
. Это означает, что с ростом цены выручка вначале увеличивается (несмотря на падение спроса) и при  достигает максимального значения, равного
достигает максимального значения, равного .
.
 , и отрицательный, пока
, и отрицательный, пока  .
. функция возрастает все медленнее. Соответствующая часть графика выпукла. Как уже отмечалось, дальнейшее повышение цены невыгодно.
функция возрастает все медленнее. Соответствующая часть графика выпукла. Как уже отмечалось, дальнейшее повышение цены невыгодно. выручка убывает все быстрее т приближается к нулю при
выручка убывает все быстрее т приближается к нулю при функция
функция  вогнута. В точке
вогнута. В точке  график перегибается (см. рис. 9).
график перегибается (см. рис. 9). , полученная от ее реализации, связаны следующей зависимостью:
, полученная от ее реализации, связаны следующей зависимостью: .
. .
. .
. рублей. Известно, что с течением времени стоимость меда повышается по закону
рублей. Известно, что с течением времени стоимость меда повышается по закону  , а затраты на хранение настолько меньше
, а затраты на хранение настолько меньше  , что ими можно пренебречь. С другой стороны, если мед продать, а деньги положить в банк, то на вырученную сумму непрерывно будут начисляться 10% годовых. То есть сумма
, что ими можно пренебречь. С другой стороны, если мед продать, а деньги положить в банк, то на вырученную сумму непрерывно будут начисляться 10% годовых. То есть сумма  , положенная в банк в момент времени
, положенная в банк в момент времени  , через
, через  лет станет равной
лет станет равной  %=
%=  ).
). , в который наиболее выгодно продать имеющийся запас меда и положить деньги в банк, чтобы через
, в который наиболее выгодно продать имеющийся запас меда и положить деньги в банк, чтобы через  лет сумма, накапливаемая на счете, была максимальной.
лет сумма, накапливаемая на счете, была максимальной. от объема производства
от объема производства  .
. ).
). .
. . При каких значениях
. При каких значениях  , где
, где  - цена. Установите вид зависимости предельного предложения (скорости изменения предложения) и темпа изменения предложения от цены на товар. Как изменение этих параметров характеризует динамику предложения?
- цена. Установите вид зависимости предельного предложения (скорости изменения предложения) и темпа изменения предложения от цены на товар. Как изменение этих параметров характеризует динамику предложения? .
.