
|
|
Переход к трехмерной псевдоматрице поля Ex12 Рогачев М.В., Монаев С. А Abstract
Методика Срединного Градиента на высокомных разрезах для инженерных задач развивается в направлении комбинации многочастотной съемки (аналог ЧЗ+ДЗ) с применением источника поля в виде заземленной питающей линии конечной длины и измерений компонент Ex (Ey), Hz на приемные диполи емкостного или электрического типа, на датчики магнитного поля. Такое совмещение геометрического и частотного принципа зондирований позволяет вести площадную съемку в движении. В физико-математическом смысле приемы интерпретации опираются на класс электродинамических задач в волновом приближении. Традиционные электродинамические задачи, исходящие из бесконечного набора решений телеграфного уравнения в виде интегральных представлений, приводят в математическом смысле к комплексным коэффициентам разложений подинтегральных выражений в ряды, с удержанием членов, пропорциональных- 1/R, 1/R2, 1/R3, вплоть до пятой степени. В теории токовой линии конечной длины (поле осциллятора), компоненты электромагнитного поля над однородным полупространством аппроксимируются разложением eikr по малому параметру kr: В теории комплексных переменных есть ряд функций называемых аналитическими. Условиям аналитичности соответствует функциональное пространство Гильберта и можно представить данные в комплексной плоскости, где полюсы, существенно особые точки и точки ветвления физически связаны с геологическими границами и поверхностями геологических тел. В окрестностях полюсов и особых точек аналитические функции и ряд Тэйлора однозначны, поэтому они представляют физический интерес. Ряд Лорана позволяет произвести классификацию особенностей нерегулярных точек. В окрестностях точки ветвления функцию нельзя разложить в указанные ряды или она является многозначной. Условия Коши-Римана, устанавливающее связь между действительно и мнимой частями аналитической функции, приводят к известным спектральным соотношениям, помогают найти фазовый спектр по его амплитудному, поскольку фактически измеряется амплитудный спектр электромагнитного поля на нескольких опорных частотах. Важно оценить две интерполянтные функции F(ω) и ln F(ω) с точки зрения аналитичности, не имеющие нулей в верхней полуплоскости Imω›0 и удовлетворяющая лемме Жордана. Для первой функции-интерполянта нужна проверка на нуль в верхней полуплоскости и если он единственный, то переходим к применению функции F(ω)=F0(ω) Переход к трехмерной псевдоматрице поля Ex Измеренное поле Exf,гц= По определению, за затухание отвечает мнимая часть волнового числа (фазовые углы), а действительная часть отвечает за длину волны и фазовую (групповую) скорость [5]. Из теории функций комплексных переменных. Если функцию можно разложить в ряд Тейлора, то она является аналитической. Ряд Тейлора позволяет найти функцию f(ω) в регулярных точках, если ее значение известно в точке ω=ω0. Все другие точки, в которых ряд Тейлора не существует, называются особенностями: полюса, существенно особые точки и точки ветвления – в них функция разрывается. На особые точки амплитудный спектр проверяется разложением в ряд Лорана.
Для полюсов ряд Лорана содержит конечное число коэффициентов ряда, для существенно особых точек ряд Лорана содержит бесконечное число членов с отрицательными степенями. В окрестностях точки ветвления функцию нельзя разложить ни в ряд Тейлора, ни в ряд Лорана. При наличии нерегулярных точек интегрирование (суммирование) ведется на основе теоремы вычетов. Как пример, можно привести аналитические функции комплексного переменного в виде многочленов от z=x+iy.
Функция ez –универсальная функция. В плоскости комплексной частоты по формуле Коши разложим спектр F(ω)=R(ω)+iIm(ω)=А(ω)eiφ(ω). Амплитудный спектр измерен в трех узловых частотных точках на плоскости XY. Ищем фазовый спектр из преобразований Гильберта.
Из-за многозначности фазовых спектров, которые отвечают за форму амплитудных спектров, следует учесть, что при преобразовании Гильберта фазовые углы испытывают разрывы при переходе через значения, кратные π. Поэтому нужно дополнить значения углов в точках разрыва значениями ±2π (функция unwrap). Основная формула спектрального анализа: Подготовительные работы. Подсчитана необходимая статистика по трем частотным срезам ρω,статистика сохранена и визуализирована для понимания типа распределения ρω. Геометрия и координаты профилей и точек измерений построены на плане и визуализированы в виде карты изоом и изоаномал.
Алгоритмические шаги.
1 шаг. Составили матрицу А(i,j,k), в координатах XYF. Задаются узловые точки или плоскости F= 4,88; 625 и 1256 Гц. Назначаем координату X(0:20:i)-вектор строка и координату Y(0:20:j)-вектор –строка, в зависимости от площади съемки и шага между профилями и точками измерений на профиле. В данном случае в основании куба задается квадратная сеть. Назначаем третью координату F=logspace(0;3,400019635;n=2512)-вектор-строка логарифмической линейки частот от декады 100 до декады 103,400019635 Гц. Удвоенная частота f =2·1256 Гц=2512 Гц. Для визуализации внутри этого диапазона декад применяется удвоенная линейка частот [1: 100: 2512] и достаточен логарифмический шаг 10 или 100 Гц. Затем понадобится сменить дискреты частоты, связанные с теоремой Котельникова (FН≤1/2t0 Найквиста) при обратном преобразовании Фурье. В узлах объемной сети находятся три значения ρω
2 шаг. Визуализация куба матрицы A с управлением прозрачностью (OpenGL) и ее вращение для рассмотрения особенностей в поведении трех частотных плоскостей ρω. Принятие предварительного решения о положении будущих линий разреза.
Для приближенного представления значений ρω в межузловых частотных точках применим полиномы Лежандра. Физико-математическое обоснование следующее. Пространство гармонических сферических функций ρω, удовлетворяют уравнению Лапласа в сферической системы координат (кроме нуля). Следовательно, одна из производящих функций (частный случай решения телеграфного уравнения) есть функция Лежандра. Полезным является ее свойство ортогональности. Другой производящей функцией может являться другая аналитическая функция. Здесь важно, что бы физическое поле было описано аналитическим представлением без лишних осцилляций и с минимальными остатками (аналог ряда Фурье).
3 шаг. Проводим узловую интерполяцию в матрице - кубе A(i,j,k) изображения ρω полиномами Лежандра (например, функцией legandre), тем самым переводим амплитудно-частотно-дискретное пространство трех узловых плоскостей в функциональное (предпочтение - нечетным функциям).
Задача 5-го шага перевести функциональное пространство ρω в пространство Гильберта.
5 шаг. Через преобразование Гильберта выделили амплитудный и фазовый спектры. Амплитудный спектр равен измеренному изображению ρω. Фазовый спектр (в радианах) вращаем функцией unwrap сначала на ±π, тем самым корректируем разрывы, свойственные преобразованию. Сохранили изображения спектров в амплитудной и фазовой матрицах A(i,j,k) и Ф(i,j,k). Визуалировали куб фазовой матрицы Ф с возможностью корректировки разрывов (возможен ввод углов ±π/2,±π/4 и других). Находим регулярные разрывы. Сохраняем матрицу Ф (ω) с фиксированными фазовыми углами- разрывами. Это путь вслепую. Задача 6-го шага - создать фазовый портрет электромагнитного поля конкретной геологической среды с контролируемым источником поля. Математически обоснованный путь ниже.
6 шаг и неоднократный возврат к 5- му шагу. На основании свойств ортогональности проводим разложение функционального пространства ρω (матрица А) полиномами Тейлора через опорные частотные точки с шагом 10 или 100, 200 Гц (предстоит выбирать, а полиноминальных членов может быть хватит 5).
Для этого в качестве смотровой площадки вводим комплексную плоскость ω= real ω+iIm ω в единичном круге. Проецируем матрицу Ф на плоскость, проверяем на верхней полуплоскости наличие нулей, полюсов и точек ветвления- ищем регулярные фазовые разрывы. Если их нет (нет границ), то F(ω) – регулярная функция и идем к пункту 7. Признак нуля. Если есть одиночные нули- F(ω)=0, при Im ω>0, то представляем функцию - спектр как Ф(ω)=lnF(ω)=lnA(ω)+iφ(ω). Перевычисляем фазовый спектр φ(ω)=-1/π∫ В случае регулярной цепочки нулей или их облака - F(ω)= F0(ω)∏ Признак полюса. Если есть полюс, то ряд Лорана имеет конечное число членов. Признак точки ветвления. Если есть точки ветвления, ряд Лорана имеет бесконечное число отрицательных степеней, рядом Тейлора амплитудный спектр не разлагается и функция многозначная в окрестностях точки ω. Сохраняем фазовый спектр Ф (в радианах) в качестве фазового портрета электромагнитного поля. Удобная визуализация куба матрицы Ф, масштабирование радиан с управлением прозрачностью (OpenGL) и ее вращение для рассмотрения особенностей в поведении аттрактора.
7 шаг. После проверки нулей и полюсов, сохранения регулярных разрывов в фазовой матрице проводим частотный срез в нужном сечении координат XYF с проверенными на регулярность и не регулярность амплитудным и фазовым спектром. Математически это означает: из трехмерных матриц A и Ф координатную выборку двухмерных спектральных значений: амплитудный- a(ω), фазовый-φ(ω) и их соединение в двухмерную матрицу Mf по правилу: амплитудно-фазовый спектр Mf= sqrt(a(ω)2+φ(ω)2). Линейка частот остается прежней. Частотный срез может проводиться неоднократно, исходя из геологической целесообразности или назначения нескольких линий проектных геологических разрезов. Задача 8-го шага вычислить фазовые задержки в радианах для получения скоростного закона
8 шаг. В двухмерной матрице φ(ω) вычислили разницу регулярных фазовых задержек на измеренных частотах 1256-625 Гц, 625-4,88 Гц и 1256-4,88 (в радианах) и сохранили в двумерной матрице Дельта Задача 9 шага - создание 2-х мерного временного разреза. Он может быть фазовый, амплитудный или амплитудно-фазовый. Назначить три кнопки- какой разрез выбираете?
9 шаг. Применили обратное двумерное преобразование Фурье к матрице Мf(f,j) и перешли от частотной к временной оси. Время назначается в микросекундах вектором размерности sizе, функция ifft2(Mf, sizе). Теорема отчетов в частотной области. Смена дискретов частоты, связанная с теоремой Котельникова (∆ω≤2π/Tc, Tc=1/2πfc, (∆f≤2πfc). Наибольшая частота, на которой измерено поле- 1256 Гц. Удвоенная (зеркальная) частота = 2512 Гц. Из-за свойств преобразований Фурье, для времени это соответствует 1/5024 =0,199044 млсек или 199,044 мксек. Шаг по оси времени или дискреты времени - из ряда 10,50 мксек. Сохранили матрицу Mt. Визуализация временного разреза-матрицы Mt с масштабированием амплитуд ρω .
10 шаг. По действительной части волнового числа и фазовым задержкам находим скорость в среде. V=30000/ Задача 11 шага - создание 2-х мерного глубинного разреза. Он может быть только амплитудно-фазовый.
11 шаг. Скорость (скоростной закон) умножаем на временную линейку в микросекундах - переводим в матрице Mt координатную ось времен в относительную координатную ось глубин в метрах (от нуля до скин-слоя, где амплитудные значения уменьшаются в exp раз (в 524 раза). Проверяем линейку глубин по формуле эффективного проникновения поля h= Задача 12 шага - облагораживание глубинного разреза – матрицы Mh. Назначение и рисовка на разрезе скважин, точек зондирований, текстов, пикетов, масштабов съемки. Втавка других уменьшенных изображений. Масштабирование амплитуд способом переменной плотности и цветом, усиление, фильтрации и т.д. с учетом бесконечного наращивания графических возможностей. Вывод на .dxf
12 шаг. Визуализируем глубинный разрез матрицы Mh, назначаем топографические отметки высот в случае пересеченного рельефа или условную линию приведения в случае спокойного рельефа, с пересчетом относительной линейке глубин в абсолютные топографические значения, если они есть. Приводим разрез к технически правильному оформлению с условными обозначениями и масштабированием.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , что приводит к спектральным выражениям для компонент Eх в виде интеграла Зоммерфельда или Фока.
, что приводит к спектральным выражениям для компонент Eх в виде интеграла Зоммерфельда или Фока. . Если ноль не единственный, то применяем модифицированную функцию F(ω)=F0(ω)∏
. Если ноль не единственный, то применяем модифицированную функцию F(ω)=F0(ω)∏  (Кауфман, 2007 г). Другими словами, проверяем наличие границ через фазовые портреты поля (странные аттракторы).
(Кауфман, 2007 г). Другими словами, проверяем наличие границ через фазовые портреты поля (странные аттракторы). , где волновое число к=
, где волновое число к= 
 =
=  +ί
+ί  в высокомных разрезах должно использоваться в стационарном смысле. A(ω), не что иное, как измеренный амплитудный спектр.
в высокомных разрезах должно использоваться в стационарном смысле. A(ω), не что иное, как измеренный амплитудный спектр.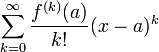


 приводит к обратным преобразованиям Фурье измеренного спектра или кепстральным преобразованиям на комплексной плоскости.
приводит к обратным преобразованиям Фурье измеренного спектра или кепстральным преобразованиям на комплексной плоскости. dω, и F(ω)= F0(ω)
dω, и F(ω)= F0(ω)  (может быть по кепстральной функции).
(может быть по кепстральной функции). (теорема вычетов).
(теорема вычетов). размерностью 3х3.
размерностью 3х3. - где V – вектор- строка для трех фазовых сдвигов, 30 000 м/мкsec– скорость электромагнитной волны в воздухе, ε- назначается относительная диэлектрическая проницаемость, ρω- из амплитудного спектра Aω по среднеквадратичному в вертикальной плоскости направлению. Рассчитать среднеквадратичные значения ρω в указанных мышью прямоугольных окнах. Например, по первой паре фазовых задержек на высоких частотах находим скорость в среде. И по второй паре фазовых задержек на низких частотах находим так же скорость в среде. При необходимости смотрим общий фазовый сдвиг на частотах 1256-4,88 Гц. Сравниваем их, если общий сдвиг примерно равен сумме двух сдвигов, значит среда является в этом диапазоне частот линейным фазовращателем. В случае явного скоростного закона V=V(t0) аппроксимируем скоростные точки простейшим полиномом и его применяем при переходе к глубинному разрезу. Принимаем решение об использовании скорости в виде одиночного значения (среда однородна) или в виде скоростного закона (среда слоистая). Время t0 – из 9-го шага. Визуализация графика V=V(t0) для вставки в визуализацию шага 12.
- где V – вектор- строка для трех фазовых сдвигов, 30 000 м/мкsec– скорость электромагнитной волны в воздухе, ε- назначается относительная диэлектрическая проницаемость, ρω- из амплитудного спектра Aω по среднеквадратичному в вертикальной плоскости направлению. Рассчитать среднеквадратичные значения ρω в указанных мышью прямоугольных окнах. Например, по первой паре фазовых задержек на высоких частотах находим скорость в среде. И по второй паре фазовых задержек на низких частотах находим так же скорость в среде. При необходимости смотрим общий фазовый сдвиг на частотах 1256-4,88 Гц. Сравниваем их, если общий сдвиг примерно равен сумме двух сдвигов, значит среда является в этом диапазоне частот линейным фазовращателем. В случае явного скоростного закона V=V(t0) аппроксимируем скоростные точки простейшим полиномом и его применяем при переходе к глубинному разрезу. Принимаем решение об использовании скорости в виде одиночного значения (среда однородна) или в виде скоростного закона (среда слоистая). Время t0 – из 9-го шага. Визуализация графика V=V(t0) для вставки в визуализацию шага 12. на трех частотах и трех среднеквадратичных эффективных сопротивлениях в разрезе. В случае их приемлемого совпадения и близких оценках, сохраняем матрицу Mh.
на трех частотах и трех среднеквадратичных эффективных сопротивлениях в разрезе. В случае их приемлемого совпадения и близких оценках, сохраняем матрицу Mh.