
|
|
Модель Леонтьева затраты-выпуск12 Глава 5. Линейные модели экономики Планирование выпуска на уровне отраслей При экономическом планировании на уровне регионов или страны в целом возникает необходимость определения объема выпуска товаров, обеспечивающего заданный спрос населения и производственные нужды на эти товары при известной технологии. В предположении о линейности технологии (т.е. о прямой пропорциональности объема выпуска объемам затрат ресурсов) математической формализацией этой задачи является знаменитая модель затраты-выпуск, полученная в 1930 г. американским экономистом В. Леонтьевым. Модель Леонтьева является частным случаем модели Вальраса. С точки зрения этой общей модели равновесия классическая (исходная) модель Леонтьева имеет следующие особенности: · рассматривается экономика, состоящая из «чистых» отраслей, т.е. когда каждая отрасль выпускает один и только свой вид продукта; · взаимосвязь между выпуском и затратами описывается линейными уравнениями (линейная и постоянная технология); · вектор спроса на товары считается заданным, т.е. в модели отсутствуют как таковые оптимизационные задачи потребителей; · вектор выпуска товаров вычисляется, исходя из спроса, т.е. отсутствуют как таковые оптимизационные задачи фирм; · равновесие понимается как строгое равенство спроса и предложения, т.е. стоимостной баланс отсутствует, более того, цены товаров в модели не рассматриваются вообще. Уравнение Леонтьева, как пример описательной модели экономики на уровне интуитивных рассуждений, было получено ранее. Приведем экономически обоснованную строгую аргументацию этой модели. Сначала рассмотрим наиболее упрощенный ее вариант. В зависимости от цели исследования экономику можно изучать в различных разрезах - от уровня национальной экономики до уровня отдельных фирм и потребителей. Целью построения модели Леонтьева является анализ перетока товаров между отраслями экономики, обеспечивающего такое функционирование производственного сектора, когда объем выпуска соответствует суммарному (т.е. производственному и конечному) спросу на товары. Поэтому экономика рассматривается в разукрупненном до уровня отраслей виде. Предполагается, что каждая отрасль является «чистой», т.е. выпускает только один и только свой продукт. Это допущение и ряд других упрощений (постоянство технологии производства, отсутствие инвестиций, игнорирование невоспроизводимых ресурсов и др.) касаются, в основном, исходной модели. Эти допущения не следует относить к недостаткам модели, ибо она в дальнейшем обобщается и конкретизируется до разных уровней детализации. Рассмотрим предпосылки модели. Все отрасли предполагаются взаимозависимыми в том смысле, что для производства своего продукта каждая из них использует результаты производства (продукты) других фирм и только их. Другими словами, на данном уровне формализации применение отраслями невоспроизводимых производственных факторов не предусматривается. Обозначим через n количество всех отраслей. Так как отрасли являются чистыми, индекс отрасли можно отождествить как с видом товара, так и с технологическим процессом. Предположим, что на данном плановом периоде времени (например, на предстоящий год) известен конечный спрос
- суммарное потребление продукции отрасли j в производственном секторе. Наглядную картину межотраслевых связей при плане выпуска
Рис. 5.1. Схема межотраслевого баланса
Балансовый характер этой схемы заключается в том, что элементы последних трех столбцов в каждой строке должны удовлетворять равенству
Левую часть равенства (5.1.1) можно трактовать как итоговый (производственный плюс конечный) спрос на продукцию отрасли j (на j-ый товар), а правую - как предложение j-го товара. Поэтому, во-первых, уравнения (5.1.1) отражают общее равновесие (т.е. равновесие по всем видам товаров) в экономике. Во-вторых, система (5.1.1) показывает самодостаточность производства - для выпуска любого товара достаточно иметь воспроизведенную продукцию рассматриваемых отраслей. В-третьих, из уравнений (5.1.1) следует, что весь валовый выпуск полностью распределяется между потребителями. Последние два обстоятельства говорят о замкнутости экономики - нет поступления извне, и продукция не экспортируется. Таким образом, схема межотраслевого баланса задает те условия, когда экономика будет находиться в равновесном состоянии. А именно, при известном спросе и известной постоянной технологии вектор валового выпуска Наиболее общая, чем изображенная на рис. 5.1, схема межотраслевого баланса, которая используется на практике, содержит дополнительные столбики учета невоспроизводимых факторов (таких, как каменный уголь), импортируемых ресурсов, а также резервов на начало планируемого периода. Эти столбики можно отнести к дополнительным (фиктивным) отраслям В целом межотраслевой баланс содержит два раздела: формирование производственных ресурсов и использование результатов производства на производственное и конечное потребление. В этом случае говорят о межотраслевом балансе в натуральном выражении. Более сложную структуру имеет схема межотраслевого баланса в денежном выражении, которая состоит из четырех разделов: промежуточного продукта, конечного продукта, амортизации, вновь созданной стоимости и ее перераспределения. Модель Леонтьева затраты-выпуск Подставляя технологические коэффициенты
С помощью технологической матрицы
эту систему уравнений можно написать в векторной форме:
Уравнение (5.2.1), где A - постоянная технологическая матрица, Модель Леонтьева отвечает на вопрос: можно ли в условиях данной технологии удовлетворить конечный спрос? Ответ на этот вопрос сводится к существованию решения системы
относительно переменных Определение 5.1. Модель Леонтьева называется продуктивной, если система (5.2.1) имеет неотрицательное решение Перепишем систему (5.2.1) в виде
где E – единичная Матрица
Для того чтобы применить эти условия существования и невырожденности к матрице Система (5.2.1) является частным случаем (при
где
где D -
Если Следовательно, если найти условия существования неотрицательного решения системы (5.2.4), то тем самым можно доказать продуктивность модели Леонтьева, получаемой из (5.2.3) при Справедливы следующие утверждения. Теорема 5.1. Матрица D системы (5.2.4) , элементы которой удовлетворяют условиям (5.2.5) , неотрицательно обратима тогда и только тогда, когда уравнение (5.2.4) имеет неотрицательное решение (т.е. продуктивно). (Квадратная матрица D называется неотрицательно обратимой, если она невырожденна и ее обратная матрица Теорема 5.2. Уравнение (5.2.4) продуктивно тогда и только тогда, когда матрица удовлетворяет условию Хокинса-Саймона, т.е. все главные ее миноры положительны. Из приведенных утверждений следует, что необходимым и достаточным условием продуктивности модели Леонтьева (5.2.1) является существование неотрицательно обратимой матрицы Следовательно, если эти условия выполнены, то искомый вектор выпуска x определяется по формуле (5.2.2). Матрица Известно, что матрицу
где
Если матрица Таким образом, для продуктивной модели Леонтьева вектор валового выпуска x представляется матричным рядом
Здесь слагаемые
с начальным условием Важным следствием модели Леонтьева являются результаты, получаемые с применением двойственной к ней модели
где Существование решения двойственного уравнения (5.2.7) относительно вектора цен связано с неотрицательностью всех его элементов. Если уравнение (5.2.7) имеет неотрицательное решение
такие что (5.2.7) является частным случаем (при Теорема 5.3. Для того чтобы модель Леонтьева (5.2.1) была продуктивной, необходимо и достаточно, чтобы двойственная к ней модель (5.2.7) была прибыльной. Здесь рассмотрена классическая (исходная) модель Леонтьева, которая описывает производство по схеме затраты-выпуск. Значимость модели Леонтьева заключается еще и в том, что она применяется для описания ряда других экономических задач, а также служит отправной точкой для различных обобщений. В качестве подтверждения этого приведем интерпретацию уравнения (5.2.1) как модели международной торговли и модификацию модели Леонтьева как оптимизационной задачи. При трактовке уравнения (5.2.1) как модели торговли n означает число торгующих между собой стран, И в такой интерпретации, очевидно, все элементы модели Леонтьева должны быть неотрицательными и, более того, национальный доход и национальные затраты всегда являются положительными величинами. В данном случае модель (5.2.1) дает ответ на вопрос: каковы должны быть объемы национальных доходов стран, обеспечивающие стабильный уровень национальных расходов и установившийся режим обмена товарами между странами? Ранее было отмечено, что одним из существенных упрощений модели Леонтьева является отсутствие в ней первичных (невозобновляемых) факторов производства. Модель будет более близкой к реальности, если наряду с воспроизводимыми (вторичными) ресурсами, описываемыми в (5.2.1) произведением Предположим, что в модели (5.2.1) каждый товар производится с использованием продукций всех отраслей и еще m видов первичных ресурсов. Обозначим через Таким образом, для каждого товара j мы имеем
Поэтому производство во всех n отраслях может быть описано n линейными производственными функциями
(здесь для всех ресурсов вида i и k , участвующих в выпуске товара вида j , предполагаются условия Из (5.2.10) и (5.2.11) следует, что для любых i и k
Поэтому справедливы уравнения:
Суммируя обе части этих уравнений по j, получим выражения, определяющие суммарные по всем отраслям объемы затрат вторичных и первичных факторов производства:
Так как уравнения (5.2.12) относятся к товарам каждой отрасли, используемым как на производственное, так и на конечное потребление, то выполняется равенство
или в матричной форме
трактуемую как технологическая матрица для первичных ресурсов, и предположим, что известен вектор
Тогда из (5.2.13) следует условие Обозначим через Поставим следующий вопрос: при каком векторе выпуска
при ограничениях
Так как по смыслу задачи максимизация дохода осуществляется через вектор выпуска, эту задачу целесообразно переписать, выразив в целевой функции вектор спроса c из уравнения (5.2.1):
при ограничениях
Напишем для (5.2.14)-(5.2.15) двойственную задачу с новой переменной
при ограничениях
Введем изменение масштаба цен
Решение задачи (5.2.18) дает вектор спроса на товары Согласно общего определения равновесия (см. раздел 4.3), набор
Благодаря линейности задач (5.2.18) и (5.2.19), такое равновесие существует. Замечание. Существование равновесия (5.2.20) можно доказать либо показав выполнение условий теоремы Эрроу-Дебре из раздела 4.4, либо доказав напрямую, применяя схему доказательства теоремы Эрроу-Дебре, т.е. приведя к теореме Какутани о неподвижной точке для полунепрерывного сверху отображения множества нормированных цен:
Планирование производства в динамике Следующим представителем класса линейных моделей экономики является модель, построенная в середине 1930-х годов австрийским математиком Джоном фон Нейманом. По сравнению с моделью Леонтьева, которую можно использовать для планирования производства на одном плановом периоде в целом (год, пятилетка и т.д.), модель Неймана отслеживает производственный процесс внутри планового периода, т.е. затраты и выпуск, осуществляемые в каждый период времени (от квартала в квартал, от года в год и т.д.). Поэтому она обобщает модель Леонтьева в двух аспектах: в динамическом плане и в плане многопродуктовых отраслей. В модели Неймана предполагается, что экономика функционирует эффективным образом сколь угодно долго. Логическим следствием такой предпосылки является рост производственных возможностей во времени с нарастающими темпами. Поэтому модель Неймана описывает расширяющуюся экономику. Модель Леонтьева фактически является аналитическим описанием схемы межотраслевого баланса. Подобно этому, модели Неймана, как отправная точка, предшествует схема динамического межотраслевого баланса. Для вывода этой схемы рассмотрим функционирование экономики на некотором конечном периоде времени
Тогда получаем последовательность полуинтервалов Будем предполагать, что экономика состоит из n чистых отраслей с постоянными технологиями, описываемыми матрицей A. Планирование опять будем понимать по схеме затраты-выпуск при известном спросе на товары, но теперь уже с учетом фактора времени. Под планом производства на отрезке времени
Здесь каждая строка соответствует плану Труд, как вид товара, не рассматривался в исходной модели Леонтьева. Особенность данного товара заключается в том, что он, во-первых, являясь воспроизводимым ресурсом, в то же время не является продуктом какой-либо отрасли, во-вторых, как фактор в производственном процессе, занимает промежуточное положение между материальными ресурсами и готовой продукцией. Никакое производство не может обходиться без трудовых затрат. Единицей ее измерения является рабочая сила. Необходимое для отрасли количество рабочей силы определяется трудовыми затратами, вложенными в выпуск одной единицы продукции. Данный параметр для отрасли j обозначим Обозначим через Наглядную картину межотраслевых связей во времени при плане производства
Рис. 5.2. Схема динамического межотраслевого баланса
Балансовый характер этой схемы заключается в том, что ее элементы должны удовлетворять следующим (балансовым) соотношениям:
Здесь Если сравнить систему (5.3.1)-(5.3.5) с моделью Леонтьева (5.2.1), то можно заметить, что последняя получается из (5.3.1) при отсутствии приращения производства, т.е. когда

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 на все n товаров. Пусть технология производства предписывает для выпуска одной единицы i -го товара
на все n товаров. Пусть технология производства предписывает для выпуска одной единицы i -го товара  количество товара вида 1,
количество товара вида 1,  количество товара вида 2 и т.д.,
количество товара вида 2 и т.д.,  количество товара вида n
количество товара вида n  Обозначим через
Обозначим через  объем производства отрасли i на всем плановом периоде (валовый выпуск). Тогда величина
объем производства отрасли i на всем плановом периоде (валовый выпуск). Тогда величина  показывает объем продукции отрасли j , необходимый для функционирования отрасли i с планом выпуска
показывает объем продукции отрасли j , необходимый для функционирования отрасли i с планом выпуска 
 и плане конечного потребления
и плане конечного потребления 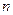





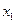












 (5.1.1)
(5.1.1) для которых
для которых  при
при  В модели (5.1.1) можно учитывать и экспорт товаров и инвестирование, фиксируя их объемы в столбике конечного потребления по видам товаров, т.е. рассматривая вместо
В модели (5.1.1) можно учитывать и экспорт товаров и инвестирование, фиксируя их объемы в столбике конечного потребления по видам товаров, т.е. рассматривая вместо  величины
величины 
 в (5.1.1), для каждой отрасли получаем балансовое соотношение
в (5.1.1), для каждой отрасли получаем балансовое соотношение

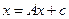 (5.2.1)
(5.2.1)
 . Условия существования и единственности решения такой системы известны из курса алгебры. Однако здесь речь идет о решении этой системы, имеющем подходящий экономический смысл. А именно, все элементы модели Леонтьева по их определению являются неотрицательными величинами, в том числе переменные
. Условия существования и единственности решения такой системы известны из курса алгебры. Однако здесь речь идет о решении этой системы, имеющем подходящий экономический смысл. А именно, все элементы модели Леонтьева по их определению являются неотрицательными величинами, в том числе переменные 
 Тогда
Тогда  или
или (5.2.1)
(5.2.1) -матрица. Следовательно, существование неотрицательного решения системы (5.2.1) определяется существованием невырожденной матрицы
-матрица. Следовательно, существование неотрицательного решения системы (5.2.1) определяется существованием невырожденной матрицы  обратной к матрице
обратной к матрице 
 называется невырожденной, если она имеет обратную матрицу
называется невырожденной, если она имеет обратную матрицу  , определяемую условиями
, определяемую условиями  Матрица B является невырожденной в том и только в том случае, если
Матрица B является невырожденной в том и только в том случае, если  где
где  - детерминант (определитель) матрицы B. Обратная матрица
- детерминант (определитель) матрицы B. Обратная матрица 
 приведем ряд дополнительных построений.
приведем ряд дополнительных построений. ) более общей системы
) более общей системы (5.2.3)
(5.2.3) Рассмотрим следующую, связанную с уравнением (5.2.3), систему
Рассмотрим следующую, связанную с уравнением (5.2.3), систему (5.2.4)
(5.2.4)
 . (5.2.5)
. (5.2.5) для всех i,j , то систему (5.2.3) можно преобразовать в (5.2.4), положив
для всех i,j , то систему (5.2.3) можно преобразовать в (5.2.4), положив  где
где  - символ Кронекера. Обратно, система (5.2.4) может быть преобразована в (5.2.3) . Для этого нужно взять достаточно большое положительное число
- символ Кронекера. Обратно, система (5.2.4) может быть преобразована в (5.2.3) . Для этого нужно взять достаточно большое положительное число 
 и положить
и положить  Отсюда
Отсюда 
 неотрицательна).
неотрицательна).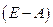 , т.е. чтобы матрица
, т.е. чтобы матрица  и чтобы обратная матрица
и чтобы обратная матрица  была неотрицательна.
была неотрицательна. вектора c и соответствующее приращение
вектора c и соответствующее приращение  вектора x связаны между собой уравнением
вектора x связаны между собой уравнением  Следовательно, матрица
Следовательно, матрица 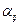 ) можно интерпретировать как количество продукта одного вида, необходимое для выпуска одной единицы продукции другого вида.
) можно интерпретировать как количество продукта одного вида, необходимое для выпуска одной единицы продукции другого вида.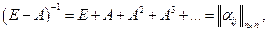

 ,
,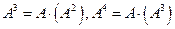 и т.д. Следовательно, вычисление (аппроксимация) обратной матрицы
и т.д. Следовательно, вычисление (аппроксимация) обратной матрицы 
 (5.2.6)
(5.2.6)
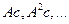 интерпретируются как промежуточные затраты, а именно,
интерпретируются как промежуточные затраты, а именно,  - затраты, необходимые для производства (выпуска) c,
- затраты, необходимые для производства (выпуска) c, 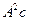 и т.д. Сумма вектора чистого выпуска c (вектора конечного потребления) и всех векторов промежуточных затрат (производственного потребления) и составляет вектор валового выпуска. Из предыдущего равенства следует, что решение уравнения (5.2.1) можно получить итерационно по формуле
и т.д. Сумма вектора чистого выпуска c (вектора конечного потребления) и всех векторов промежуточных затрат (производственного потребления) и составляет вектор валового выпуска. Из предыдущего равенства следует, что решение уравнения (5.2.1) можно получить итерационно по формуле

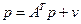 , (5.2.7)
, (5.2.7) - транспонированная матрица A . Уравнению (5.2.7) можно придать смысловую стоимостную окраску. Действительно,
- транспонированная матрица A . Уравнению (5.2.7) можно придать смысловую стоимостную окраску. Действительно,  можно интерпретировать как вектор цен продуктов отраслей,
можно интерпретировать как вектор цен продуктов отраслей,  - как вектор добавленной стоимости (т.е. прибавка к стоимости товара после ее производства) на единицу выпуска,
- как вектор добавленной стоимости (т.е. прибавка к стоимости товара после ее производства) на единицу выпуска,  - как вектор суммы издержек на единицу выпуска. Тогда разность
- как вектор суммы издержек на единицу выпуска. Тогда разность  есть вектор чистого дохода от единицы выпуска. Этот чистый доход и приравнивается добавленной стоимости
есть вектор чистого дохода от единицы выпуска. Этот чистый доход и приравнивается добавленной стоимости  .
. (5.2.8)
(5.2.8) где
где 
 (5.2.9)
(5.2.9) справедливы утверждения, аналогичные теоремам 5.1 и 5.2., а также следующая теорема.
справедливы утверждения, аналогичные теоремам 5.1 и 5.2., а также следующая теорема. , будут учтены и первичные факторы. Оказывается, такое обобщение превращает модель Леонтьева в оптимизационную задачу.
, будут учтены и первичные факторы. Оказывается, такое обобщение превращает модель Леонтьева в оптимизационную задачу. количество k-го первичного фактора, затрачиваемого в производство
количество k-го первичного фактора, затрачиваемого в производство  количества j-го товара, а через
количества j-го товара, а через  - количество k -го первичного фактора, необходимое для производства одной единицы товара вида j . Из определения этих величин следует, что, как и в случае вторичных ресурсов, имеет место выражение
- количество k -го первичного фактора, необходимое для производства одной единицы товара вида j . Из определения этих величин следует, что, как и в случае вторичных ресурсов, имеет место выражение 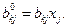
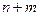 видов представления его выпускаемого объема:
видов представления его выпускаемого объема: (5.2.10)
(5.2.10) (5.2.11)
(5.2.11) ).
).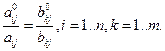


 (5.2.12)
(5.2.12) (5.2.13)
(5.2.13)
 Введем в рассмотрение матрицу
Введем в рассмотрение матрицу
 запасов всех первичных ресурсов, т.е.
запасов всех первичных ресурсов, т.е.

 векторы цен вторичных и первичных ресурсов соответственно.
векторы цен вторичных и первичных ресурсов соответственно.

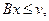

 (5.2.14)
(5.2.14) (5.2.15)
(5.2.15) (5.2.16)
(5.2.16) (5.2.17)
(5.2.17)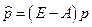 и запишем двойственные задачи (5.2.14)-(5.2.15) и (5.2.16)-(5.2.17) в более компактном виде:
и запишем двойственные задачи (5.2.14)-(5.2.15) и (5.2.16)-(5.2.17) в более компактном виде: при ограничениях
при ограничениях  (5.2.18)
(5.2.18) (5.2.19)
(5.2.19)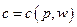 , а решение задачи (5.2.19) - вектор предложения первичных факторов
, а решение задачи (5.2.19) - вектор предложения первичных факторов  Для пары задач (5.2.18) и (5.2.19) и их решений c и v верны все утверждения из для двойственных задач линейного программирования.
Для пары задач (5.2.18) и (5.2.19) и их решений c и v верны все утверждения из для двойственных задач линейного программирования. будет равновесным в модели Леонтьева, если выполнены соотношения
будет равновесным в модели Леонтьева, если выполнены соотношения (5.2.20)
(5.2.20)
 . Отрезок
. Отрезок  так, чтобы получилась возрастающая последовательность моментов времени
так, чтобы получилась возрастающая последовательность моментов времени .
. длины
длины  , покрывающих весь отрезок
, покрывающих весь отрезок  будем трактовать как начальный момент планирования производства товаров, а момент
будем трактовать как начальный момент планирования производства товаров, а момент  - как плановый горизонт. В дальнейшем во всех отношениях удобно полагать
- как плановый горизонт. В дальнейшем во всех отношениях удобно полагать  и трактовать моменты
и трактовать моменты  как годы. При этих обозначениях будем писать
как годы. При этих обозначениях будем писать  .
.
 в год t ;
в год t ;  - вектор запасов товаров,
- вектор запасов товаров,  - вектор валового выпуска. Каждая компонента
- вектор валового выпуска. Каждая компонента  считается максимально возможным при существующих основных фондах выпуском отрасли j. Валовый выпуск отрасли может быть увеличен путем дополнительных вложений, и этот показатель также включается в план. Вектор
считается максимально возможным при существующих основных фондах выпуском отрасли j. Валовый выпуск отрасли может быть увеличен путем дополнительных вложений, и этот показатель также включается в план. Вектор 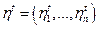 обозначает планируемое в год t увеличение (приращение) валового выпуска. Наконец, число
обозначает планируемое в год t увеличение (приращение) валового выпуска. Наконец, число  показывает общее количество нанятых во всех отраслях рабочих в год t.
показывает общее количество нанятых во всех отраслях рабочих в год t. . Тогда число рабочих в отрасли j в год t равно
. Тогда число рабочих в отрасли j в год t равно  . Вектор
. Вектор  называется вектором трудовых затрат.
называется вектором трудовых затрат. ,
,  объемы материальных затрат, необходимых для приращения на одну единицу выпуска товара i. Тогда материальные затраты на одновременное приращение выпусков всех отраслей на величины
объемы материальных затрат, необходимых для приращения на одну единицу выпуска товара i. Тогда материальные затраты на одновременное приращение выпусков всех отраслей на величины  будут исчисляться как
будут исчисляться как  , где
, где  - технологическая матрица приращения производства.
- технологическая матрица приращения производства. , плане конечного потребления на одного работающего на весь плановый период
, плане конечного потребления на одного работающего на весь плановый период  , причем при
, причем при 
 есть валовый выпуск отрасли j к началу планового периода
есть валовый выпуск отрасли j к началу планового периода









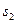
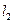
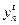



 (5.3.1)
(5.3.1)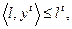 (5.3.2)
(5.3.2) (5.3.3)
(5.3.3) (5.3.4)
(5.3.4) (5.3.5)
(5.3.5) - производственные затраты,
- производственные затраты,  , а
, а  - конечное потребление в год t. Поэтому условие (5.3.1) требует, чтобы весь годичный запас товаров покрывал все годичные затраты ежегодно. Неравенство (5.3.2) задает условие на необходимый объем трудовых ресурсов, неравенство (5.3.3) говорит о том, что запасы на данный год не могут превышать результатов производства предыдущего года, и, наконец, уравнение (5.3.4) описывает динамику роста валового выпуска из года в год.
- конечное потребление в год t. Поэтому условие (5.3.1) требует, чтобы весь годичный запас товаров покрывал все годичные затраты ежегодно. Неравенство (5.3.2) задает условие на необходимый объем трудовых ресурсов, неравенство (5.3.3) говорит о том, что запасы на данный год не могут превышать результатов производства предыдущего года, и, наконец, уравнение (5.3.4) описывает динамику роста валового выпуска из года в год. . Дополнительные условия (5.3.2)-(5.3.4) вызваны необходимостью учета трудовых ресурсов и динамического характера развития производства. Как и модель Леонтьева, данная схема может быть обобщена и детализирована по ряду параметров. В приведенном здесь виде наиболее нереальным является условие (5.3.4), которое предполагает (при
. Дополнительные условия (5.3.2)-(5.3.4) вызваны необходимостью учета трудовых ресурсов и динамического характера развития производства. Как и модель Леонтьева, данная схема может быть обобщена и детализирована по ряду параметров. В приведенном здесь виде наиболее нереальным является условие (5.3.4), которое предполагает (при  ) получение результатов от затрат, осуществляемых в начале периода
) получение результатов от затрат, осуществляемых в начале периода  , уже к концу этого периода. Условие (5.3.4) можно записать в виде:
, уже к концу этого периода. Условие (5.3.4) можно записать в виде: