
|
|
Понятие оптимальности стратегииГлава 5. Элементы теории игр
На практике часто встречаются ситуации, когда приходится принимать решение в условиях конфликта интересов нескольких участников события. Такие ситуации возникают, например, в карточных играх, шахматах и т.п. В экономике конфликтные ситуации возникают при взаимодействии покупателя и продавца, банка и клиента, поставщика и потребителя и т.д. Особенностью подобных ситуаций является неопределенность, вызванная неизвестным заранее поведением участников конфликта, которые стремятся добиться максимальной реализации своих целей. Математическим описанием конфликтных ситуаций теория игр. Её целью является выработка рекомендаций по разумному поведению участников конфликта.
Основные понятия и общая классификация игр
Всякая математическая модель социально-экономического явления или конфликта должна выражать присущие ему черты, т.е. по крайней мере, отражать следующие его компоненты: а) заинтересованность сторон; б) возможные действия каждой из сторон; в) интересы сторон. Дадим формальное описание указанных компонент конфликта, вводя при этом принятую терминологию и обозначения. Заинтересованные стороны будем называть игроками или лицами, а множество всех игроков будем обозначать через Любое возможное для игрока Множество всех стратегий игрока Заинтересованность игроков выражается в том, что каждому игроку В этих условиях протекание конфликта состоит в выборе каждым игроком
ОпределениеИгрой называется действительный или формальный конфликт, в котором имеется, по крайней мере, два игрока, каждый из которых стремится к достижению собственных целей. Игра как процесс представляет собой многократно повторяющийся выбор игроками своих стратегий, т.е. игру следует считать не как однократный обмен ходами, а как постоянно или, по крайней мере, многократно, осуществляемый процесс. ОпределениеИгра называется игрой с нулевой суммой, если сумма всех платежей равна нулю, т.е. если сумма проигрышей проигравших игроков равна сумме выигрышей остальных игроков из множества Вообще говоря, оценка игроком Все игры можно разделить на два типа: коалиционные и бескоалиционные. Коалицией называют любое подмножество множества Среди всех бескоалиционных игр с нулевой суммой естественным образом выделяется класс антагонистических игр, в которых число игроков равно двум, а значения их функций выигрыша в каждой ситуации равны по величине и противоположны по знаку:
Для сокращения обозначений, множества стратегий игроков 1 и 2 антагонистической игре будем обозначать через Для антагонистических игр с двумя игроками вводится следующее определение. ОпределениеПусть каждой стратегии 1-го игрока взаимнооднозначно поставлена в соответствие строка некоторой матрицы Следовательно, антагонистическая игра полностью описывается единственной платёжной матрицей и в соответствии с этим называется матричной. Пример 1.Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен. Однако можно предположить, что его величина характеризуется тремя возможными состояниями (I, II, III). С учетом этих состояний анализируются три возможных варианта выпуска данной модели
Выбор в том или ином смысле наилучшего варианта выпуска моделей можно понимать как матричную игру.
Понятие оптимальности стратегии
Теория игр как математическая дисциплина в ее современном состоянии занимается нормативным изучением игр, т.е. считает своей задачей установить какое поведение игроков следует считать оптимальным (разумным, целесообразным). Оптимальность стратегии очевидно можно понимать по-разному, т.е. понятия оптимальности в теории игр и оптимального решения игры не являются однозначными, априорными, абсолютными. Вместе с тем эти понятия являются объективными, т.е. каждый вариант оптимальности поддается точному описанию при помощи математических формулировок. Тем самым различные содержательные представления об оптимальности могут приводить к отличающимся математическим моделям. Основными содержательными чертами оптимальности в применении к исходу или к множеству исходов конфликта можно считать интуитивные представления о выгодности и справедливости. Можно, например, оптимальной ситуацией считать такую, в которой одновременно достигают своих максимумов функции выигрыша каждого из игроков. Условие оптимальности в этом смысле для ситуации
Выгодность такой ситуации очевидна. Нетрудно видеть, однако, что существование в бескоалиционной игре ситуаций, оптимальных в только что описанном смысле, является сравнительно редким исключением (как и любое совпадение максимумов нескольких функций). В сущности, реализуемость этого принципа оптимальности соответствует слабости конфликтных черт моделируемого явления, близости целей его участников. Поэтому естественно поискать другие представления об оптимальности, быть может, не столь бесспорные, но зато более часто реализуемые. Одной из наиболее плодотворных форм реализации представлений об оптимальности можно считать понятие равновесия, состоящее в следующем. ОпределениеСитуация называется равновесной, если ни один из игроков не заинтересован в том, чтобы ее нарушить, т.е. отклониться от нее. Если игра
при любых ОпределениеВ случае антагонистической игры ситуация равновесия называется седловой точкой. Оказывается, что функция выигрыша игры во всех ее седловых точках принимает одно и то же значение, которое называется ценой игры (или значением игры). Именно ситуации равновесия могут быть предметом устойчивых договоров между игроками. Всякая попытка зафиксировать в договоре неравновесную ситуацию будет означать, что хотя бы у одной из договаривающихся сторон найдется такая стратегия, что выбор ее вместо предусмотренной договором увеличит выигрыш этого игрока. Тем самым возникают мотивы к нарушению договора. Обычно именно равновесные стратегии считают оптимальными и называют их решением игры. Принцип оптимальности в бескоалиционной игре, состоящий в осуществлении игроками ее ситуаций равновесия, является более слабым и чаще реализуемым, чем принцип выражаемый соотношением (2). Однако равновесные ситуации определяемые соотношением (2) так же существуют не для всякой игры. Оказывается из этой ситуации также можно попытаться найти выход. При отсутствии в игре ситуаций равновесия, при использовании игроками единственной стратегии (из имеющихся у каждого из них множества), естественно поставить вопрос о расширении понятия стратегии таким образом, чтобы среди ситуаций, составленных из новых, обобщенных стратегий все же могли бы найтись равновесные. ОпределениеЭлементы множества ОпределениеВектор Из сформулированного определения непосредственно следует, что сумма компонент указанного вектора равна единице, а сами компоненты не отрицательны. Очевидно так же, что чистую стратегию можно рассматривать как частный случай смешанной. Удобной интерпретацией смешанной стратегии является ее представление как случайного выбора игроком своих чистых стратегий в соответствии с вероятностями задаваемыми относительными частотами (вспомним «классическое определение вероятности события»). Причем выборы игроков независимы, а выигрыш в ситуации в смешанных стратегиях определяется как математическое ожидание случайного выигрыша.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
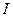 . Ограничимся рассмотрением случая, когда множество
. Ограничимся рассмотрением случая, когда множество 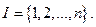
 действие называется его стратегией.
действие называется его стратегией. обозначим через
обозначим через  . В условиях конфликта каждый игрок
. В условиях конфликта каждый игрок  в результате чего складывается набор стратегий
в результате чего складывается набор стратегий 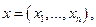 называемый ситуацией. Множество всех ситуаций обозначим
называемый ситуацией. Множество всех ситуаций обозначим  .
.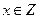 приписывается число, выражающее степень удовлетворения его интересов в этой ситуации. Это число называется выигрышем игрока
приписывается число, выражающее степень удовлетворения его интересов в этой ситуации. Это число называется выигрышем игрока 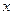 и обозначается через
и обозначается через  . Величина
. Величина 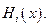 Таким образом множество игроков, их стратегий и их функций выигрыша полностью описывают некоторую игру
Таким образом множество игроков, их стратегий и их функций выигрыша полностью описывают некоторую игру  , что формально записывают так
, что формально записывают так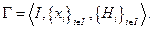 (1)
(1) не всегда возможна практически и даже не всегда имеет смысл. На этом пути создается теория игр с предпочтениями, более широкая, чем теория игр с выигрышами. В дальнейшем будем рассматривать только теорию игр с выигрышами.
не всегда возможна практически и даже не всегда имеет смысл. На этом пути создается теория игр с предпочтениями, более широкая, чем теория игр с выигрышами. В дальнейшем будем рассматривать только теорию игр с выигрышами.
 , а функция выигрыша
, а функция выигрыша  - через
- через 
 , а каждой стратегии 2-го игрока взаимнооднозначно поставлен в соответствие столбец этой матрицы. Матрицу
, а каждой стратегии 2-го игрока взаимнооднозначно поставлен в соответствие столбец этой матрицы. Матрицу 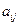 равен выигрышу 1-го игрока (т.е. проигрышу 2-го) при выборе 1-м игроком
равен выигрышу 1-го игрока (т.е. проигрышу 2-го) при выборе 1-м игроком 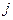 -й.
-й. . Каждый из этих вариантов требует своих затрат и обеспечивает в конечном счете различный эффект. Прибыль (тыс. р.), которую получает предприятие при данном объеме выпуска модели и соответствующем состоянии спроса, определяется матрицей
. Каждый из этих вариантов требует своих затрат и обеспечивает в конечном счете различный эффект. Прибыль (тыс. р.), которую получает предприятие при данном объеме выпуска модели и соответствующем состоянии спроса, определяется матрицей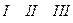
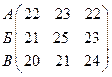
 для игры (1) формально можно записать как
для игры (1) формально можно записать как для любых
для любых  (2)
(2)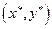 и формально для равновесной ситуации можно записать
и формально для равновесной ситуации можно записать (3)
(3) Уже из того, что в (3) используется не строгое неравенство «меньше или равно
Уже из того, что в (3) используется не строгое неравенство «меньше или равно  » следует, что равновесных ситуаций может быть несколько.
» следует, что равновесных ситуаций может быть несколько. и
и 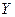 называют чистыми стратегиями игроков.
называют чистыми стратегиями игроков.