
|
|
Краткий анализ других видов дуополииРавновесие Штакельберга. Рассмотренная модель Курно описывает лишь один из возможных способов формирования экономической стратегии дуополистов. Причем исходная гипотеза (7.3.3) относительно предположительных вариаций, на основе которой строится равновесие Курно, оказалась, по существу, не соответствующей реальности, так как не выдерживает испытания временем. Откажемся от гипотезы Курно и анализируем другую гипотезу, которая порождает так называемую дуополию Штакельберга. Фирму 1 (2) будем называть дуополистом Курно, если
Далее фирму 1 (2) будем называть S-стратегом, если она считает, что фирма 2 (1) будет вести себя как дуополист Курно, т.е. что она будет определять свой выпуск, пользуясь кривой реакции Определение 7.4. Модель (7.3.1) называется дуополией Штакельберга, если одна или обе фирмы являются S-стратегами. Тройка Проанализируем дуополию Штакельберга на примере 8.2. Пусть фирма 1 является S-стратегом, т.е., по ее мнению,
Отсюда вычислим предположительную вариацию фирмы 1 для данного случая:
Подставляя это в первое из необходимых условий (7.3.9), получаем
Это равенство дает нам вид кривой реакции
Итак, если с точки зрения фирмы 1 ее партнер является дуополистом Курно, то кривые реакции имеют вид (7.4.1) и (7.4.2). Если предположение фирмы 1 верно, то, решая систему (7.4.1)-(7.4.2) относительно
Подставляя эти значения в формулу для цены
Найденная тройка
определяет равновесие Штакельберга, когда фирма 1 является объективным S-стратегом. Это равновесие часто называют 1-равновесием Штакельберга. Сравнивая данное равновесие с равновесием Курно (7.3.11), можем сказать, что в 1-равновесии Штакельберга товар "дороже" на величину Если фирмы поменяются местами, т.е. S-стратегом будет теперь фирма 2, то, учитывая симметричность случая, получим следующее 2-равновесие Штакельберга:
В этой ситуации в более выгодном положении находится фирма 2, так как она получает большую прибыль, чем в равновесии Курно, а фирма 1 - меньшую. Предположим, наконец, что обе фирмы являются S-стратегами. В результате получаем, что обе фирмы ошибаются в своих предположениях о том, что конкурент является дуополистом Курно, тогда как обе они являются истинными дуополистами Штакельберга (стратегами). В этом случае (гипотетические) кривые реакции (Курно) имеют вид:
Поэтому предположительные вариации придают необходимым условиям (7.3.9) следующий вид:
Решая совместно эти два уравнения, получаем
Этим выпускам соответствует цена
Тройка
называется неравновесием Штакельберга. Неравновесность набора (7.4.5) объясняется тем, что в данной ситуации обе фирмы получают меньшую прибыль, чем в равновесии Курно (7.3.11), и потому почти наверняка подобные экономические решения дуополистами будут отвергнуты. Равновесие Нэша. В рассмотренных моделях исходили из того, что свои экономические решения по поводу объемов выпуска дуополисты принимают лишь на основе информации (гипотезы) об объемах выпуска конкурента. Отмечая узость такого подхода, все же надо понимать, что, во-первых, всегда можно обобщить эти подходы на основе более разнообразной информации, во-вторых, объем выпуска партнера для конкурирующих фирм является основным и определяющим ориентиром для принятия решения дуополистами. Обобщая экономические решения, проанализированные в дуополиях Курно и Штакельберга, можно сказать, что у каждой фирмы есть два варианта поведения: либо действовать как дуополист Курно, либо действовать как дуополист Штакельберга (т.е. быть S-стратегом). Экономическое решение i-ой фирмы, характеризующее ее как дуополиста Курно, будем называть ее Таким образом, у каждого дуополиста имеется две стратегии: у фирмы 1 -
Рис. 7.8 Объёмы выпуска дуополистов
На рис. 7.8 Матрицу
можно рассматривать как математическую модель принятия решения с двумя участниками, имеющими каждый только две стратегии. Каждой из перечисленных четырех ситуаций соответствует одна из пар выпусков Модель (7.4.6) называется бескоалиционной игрой двух лиц или биматричной игрой; участники называются игроками, а выпуск Таким образом, биматричная игра (7.4.6) может рассматриваться как еще одна (обобщенная) модель дуополии. По построению этой игры оптимальные стратегии (стратегии, максимизирующие выигрыши) игроков являются наилучшими экономическими решениями дуополистов. Специфика модели (7.4.6), и вообще игровых моделей, в том, что по причине конфликтного характера принятия решения нет ситуаций, доставляющих игрокам их максимальные выигрыши. Объясним это на числовых значениях элементов матрицы
Следовательно, максимальный выигрыш первого игрока (36) может реализоваться в ситуации Единственным приемлемым принципом оптимального поведения игроков в биматричной игре является принцип равновесия по Нэшу (см. определение 7.1). Применяя это правило, найдем ситуацию равновесия Нэша в игре Выбирая стратегию Напомним, что эта же ситуация Картельные принципы. Приведенный выше анализ модели (7.4.7) приводит к идее о целесообразности кооперации между дуополистами с целью максимизации общей прибыли, т.е. образования картеля. В примере 8.2 объединение фирм в картель означает, что они сообща определяют объем выпуска
С помощью необходимых условий первого порядка можно найти максимальный суммарный выпуск
Следовательно, в условиях картеля нет проблем с получением максимальной суммарной прибыли, так как информация полная и нет нужды анализировать разные гипотезы. Зато здесь возникает другая проблема, связанная со справедливым разделом общей прибыли между участниками картеля. Этот вопрос напрямую приводит к теории кооперативных игр, где разработано большое число фундаментальных принципов оптимальности, таких как с-ядро, НМ-решение и т.д. Нетрудно заметить, что все дележи
Геометрически это есть отрезок, соединяющий монопольные точки
Легко убедиться, что любая точка 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



 (см. рис. 7.7).
(см. рис. 7.7).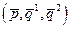 , где
, где  - решение задачи (7.3.1) при условиях дуополии Штакельберга,
- решение задачи (7.3.1) при условиях дуополии Штакельберга,  - соответствующая этим выпускам (в силу системы (7.3.1)) цена товара, называется равновесием Штакельберга.
- соответствующая этим выпускам (в силу системы (7.3.1)) цена товара, называется равновесием Штакельберга. Тогда из второго равенства в (7.3.10) найдем вид кривой реакции
Тогда из второго равенства в (7.3.10) найдем вид кривой реакции  для фирмы 2:
для фирмы 2: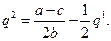 (7.4.1)
(7.4.1)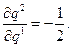
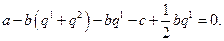
 для фирмы 1:
для фирмы 1: (7.4.2)
(7.4.2) и
и 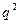 , найдем оптимальные выпуски в дуополии Штакельберга, в которой фирма 1 является S-стратегом:
, найдем оптимальные выпуски в дуополии Штакельберга, в которой фирма 1 является S-стратегом:
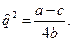
 (см. условие примера 8.2), найдем
(см. условие примера 8.2), найдем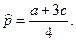
 (7.4.3)
(7.4.3) , фирма 1 выпускает больше, а фирма 2 - меньше, чем при равновесии Курно, и в таком же отношении находятся прибыли фирм.
, фирма 1 выпускает больше, а фирма 2 - меньше, чем при равновесии Курно, и в таком же отношении находятся прибыли фирм. (7.4.4)
(7.4.4)
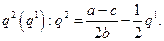
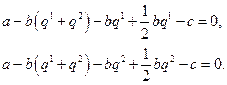
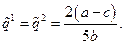
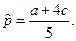
 (7.5.4)
(7.5.4) -стратегией и обозначать
-стратегией и обозначать  . Аналогично, экономическое решение i-ой фирмы, характеризующее ее как дуополиста Штакельберга, будем называть ее
. Аналогично, экономическое решение i-ой фирмы, характеризующее ее как дуополиста Штакельберга, будем называть ее  -стратегией и обозначать
-стратегией и обозначать  .
. и
и  , у фирмы 2 -
, у фирмы 2 -  и
и 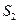 , и потому может быть реализована одна из четырех ситуаций:
, и потому может быть реализована одна из четырех ситуаций: 


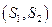 . Разместим соответствующие этим ситуациям объемы выпусков фирмы 1 и фирмы 2 в следующую таблицу (рис. 7.8).
. Разместим соответствующие этим ситуациям объемы выпусков фирмы 1 и фирмы 2 в следующую таблицу (рис. 7.8).

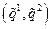
 (7.4.6)
(7.4.6)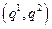 . Например, если первый участник выбрал стратегию
. Например, если первый участник выбрал стратегию 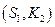 выпуск первого участника равен
выпуск первого участника равен  , а второго -
, а второго -  . Каждый участник выбирает свою стратегию с целью получения как можно большего выпуска.
. Каждый участник выбирает свою стратегию с целью получения как можно большего выпуска. , положив в примере 8.2
, положив в примере 8.2  . В этом случае матрица
. В этом случае матрица  (7.4.7)
(7.4.7) . Так как эти ситуации не совместны, т.е. не могут реализоваться одновременно, то добиться максимальных выигрышей оба игрока одновременно не смогут.
. Так как эти ситуации не совместны, т.е. не могут реализоваться одновременно, то добиться максимальных выигрышей оба игрока одновременно не смогут. а, применяя стратегию
а, применяя стратегию 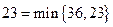 . Лучший из двух худших выигрышей равен
. Лучший из двух худших выигрышей равен  Этот выигрыш соответствует стратегии
Этот выигрыш соответствует стратегии  , в которой оба дуополиста получают большие прибыли. Но в модели (7.4.7) в условиях отсутствия обмена информацией между игроками ситуация
, в которой оба дуополиста получают большие прибыли. Но в модели (7.4.7) в условиях отсутствия обмена информацией между игроками ситуация 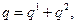 максимизирующий общую прибыль
максимизирующий общую прибыль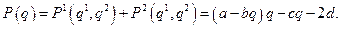
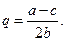 (7.4.8)
(7.4.8)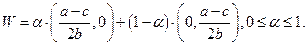
 и
и 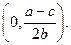
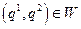 удовлетворяет условию оптимальности по Парето. Поэтому
удовлетворяет условию оптимальности по Парето. Поэтому  есть Парето-оптимальное множество распределений выпуска (7.4.8) между дуополистами и, как было замечено ранее (см. раздел 6.4), точки именно этого множества должны быть предметом переговоров по поводу справедливого дележа общей прибыли.
есть Парето-оптимальное множество распределений выпуска (7.4.8) между дуополистами и, как было замечено ранее (см. раздел 6.4), точки именно этого множества должны быть предметом переговоров по поводу справедливого дележа общей прибыли.