
|
|
Контур с активным сопротивлениемКолебания и волны Колебательным движением или колебанием называются движения или процессы, которые характеризуются повторяемостью во времени тех или иных значений физических величин. Колебательные процессы широко распространены в природе и технике и представляют собой сложные процессы. Физическая природа может быть разной, поэтому различаются: механические, электромагнитные и т.д., но различные колебательные процессы описываются одинаковыми характеристиками и однотипными уравнениями.
Для возбуждения и поддерживания электромагнитных колебаний используется колебательный контур – это цепь, состоящая из последовательно соединенных: катушки, конденсатора и сопротивления.
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис.1).
Рисунок 1. Затухающие колебания в контуре. Таким образом, затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Затухание механических колебаний вызывается трением; в электрических колебательных системах – тепловыми потерями на активном сопротивлении R, а также потерями в диэлектриках и ферромагнетиках, вследствие гистерезиса. Отношение амплитуд двух последующих затуханий называется декрементом затухания, а логарифм – логарифмическим декрементом затухания:
Ne – число колебаний, совершаемых за время уменьшения амплитуды в е раз. Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: Fтр = – rυ. Коэффициент r в этой формуле аналогичен сопротивлению R в электрическом контуре. сопротивления R контура. Интервал времени, в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.
Колебания, возникающие под действием внешней периодически изменяющейся силы или э.д.с., называются вынужденными колебаниями. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающих колебаний w0 к частоте, равной или близкой к собственной частоте колебательной системы, называется резонансом. Резонансная частота равна
Где b = R/2L. При b2 << w02 значение wрез практически совпадает с собственной частотой колебательной системы. Добротность характеризует резонансные свойства колебательной системы, чем больше Q, тем больше Арез. (Чем меньше затухание, тем больше добротность Q). Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:
Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен. Переменный ток
Электрический ток, величина и направление которого изменяется во времени называется переменным. В сеть с переменным напряжением, изменяющимся по закону В этой теме строчными буквами обозначены мгновенные значения напряжения u, тока i, мощности p; прописными буквами с нижним индексом m – амплитудные значение соответствующих величин (Um, Im, Pm); прописными буквами без индекса – эффективные значения напряжения Для мгновенных значений выполняются законы постоянного тока – закон Ома, правила Кирхгофа и закон Джоуля-Ленца. Требуется найти связь между амплитудными значениями тока и напряжения в рассматриваемом контуре, а также сдвиг фаз между током и напряжением. Контур с активным сопротивлением
Контур с электроемкостью
Формулу
Условие Зависимость тока и напряжения на конденсаторе изображены на графике. Контур с индуктивностью
Интегрируя это уравнение, получим зависимость мгновенного значения силы тока от времени:
Формулу
который можно интерпретировать как закон Ома для участка цепи с индуктивностью. Здесь
Зависимость тока и напряжения на индуктивности изображены на графике. Емкостное и индуктивные сопротивления называют реактивными, сопротивление R - активным сопротивлением. Реактивное сопротивление измеряют в тех же единицах, что и активное. Но между ними существует и принципиальное различие, а именно: только активное сопротивление определяет необратимые процессы в цепи, такие например, как преобразование электромагнитной энергии в джоулеву теплоту. Последовательное соединение R, L, C в цепи переменного тока. Закон Ома
При последовательном соединении токи, протекающие по всем элементам цепи, одинаковы, а мгновенные значения напряжений складываются, то есть
Таким образом, в результате сложения трех колебаний получается четвертое. Для сложения колебаний применим метод векторных диаграмм. Вы разим амплитудные значения напряжений на участках цепи через амплитудные значения силы тока:
Выделим направление и обозначим его как ось токов. Поскольку сдвиг фаз между током и напряжением на активном сопротивлении равен нулю, вектор напряжения длиной, равной амплитуде
Подставим в эту формулу выражения (1)
откуда выразим амплитуду силы тока
Эту формулу можно записать в виде
она представляет закон Ома для участка цепи, содержащего последовательно соединенные активное, емкостное и индуктивное сопротивления. Величину
называют полным сопротивлением цепи переменного тока или импедансом. С помощью векторной диаграммы найдем сдвиг фаз между током и напряжением:
В практике широко применяют так называемый коэффициент мощности, равный
При резонансе полное сопротивление цепи минимально и равно активному сопротивлению: Z = R, сдвиг фаз между током и напряжением равен нулю. Параллельное соединение R, L, C в цепи переменного тока
Таким образом, в результате сложения трех колебаний получается четвертое. Также, как и раньше, для сложения колебаний применим метод векторных диаграмм. По закону Ома для участков цепи имеем
Выделим направление и обозначим его как ось напряжений. Поскольку сдвиг фаз между током и напряжением на активном сопротивлении равен нулю, вектор тока длиной, равной амплитуде
Подставим в эту формулу выражения (1)
откуда выразим амплитуду напряжения
Эту формулу можно записать в виде
она представляет закон Ома для участка цепи, содержащего параллельно соединенные активное, емкостное и индуктивное сопротивления. Величину
называют полным сопротивлением цепи переменного тока или импедансом. Из векторной диаграммы видно, что при выполнении условия
Комбинированное соединение R, L, C в цепи переменного тока
Фактически “чистых” индуктивностей в природе не существует, любая катушка индуктивности обладает омическим (активным) сопротивлением. Поэтому катушку можно рассматривать как последовательно соединенные индуктивность и активное сопротивление. Рассмотренный выше случай предполагает малость активного сопротивления катушки по сравнению с ее индуктивным сопротивлением.
Связь между амплитудными значениями тока и напряжения на катушке выражается законом Ома
а сдвиг фаз между током и напряжением соотношением
причем напряжение опережает ток. Построим векторную диаграмму для параллельного соединения катушки и конденсатора. Как и раньше, выберем ось напряжений и построим векторы токов

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|



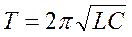 -формула Томпсона
-формула Томпсона





















 , включают следующие элементы: активное сопротивление R, катушку индуктивности L, электроемкость C. Рассматриваемый контур может содержать как один элемент, так и группу элементов. В последнем случае опишем случаи последовательного и параллельного соединения элементов.
, включают следующие элементы: активное сопротивление R, катушку индуктивности L, электроемкость C. Рассматриваемый контур может содержать как один элемент, так и группу элементов. В последнем случае опишем случаи последовательного и параллельного соединения элементов.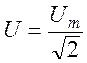 и тока
и тока  , а также среднюю мощность переменного тока P.
, а также среднюю мощность переменного тока P. Применим II правило Кирхгофа:
Применим II правило Кирхгофа:  , откуда мгновенное значение силы тока
, откуда мгновенное значение силы тока  , или
, или 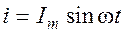 . Следовательно,
. Следовательно, ,
,  .
. Условие
Условие  означает, что ток и напряжение в одни и те же моменты времени принимают максимальные значения, в одни и те же моменты времени равны нулю. Зависимость тока и напряжения на активном сопротивлении изображены на графике.
означает, что ток и напряжение в одни и те же моменты времени принимают максимальные значения, в одни и те же моменты времени равны нулю. Зависимость тока и напряжения на активном сопротивлении изображены на графике.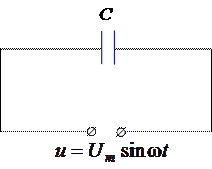 Применим II правило Кирхгофа:
Применим II правило Кирхгофа:  Из определения электроемкости
Из определения электроемкости  следует, что
следует, что  Учитывая определение силы тока
Учитывая определение силы тока  получим зависимость мгновенного значения силы тока от времени:
получим зависимость мгновенного значения силы тока от времени: , или
, или  . Следовательно,
. Следовательно,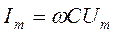 ,
, 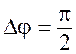 .
. можно записать в виде
можно записать в виде ,
, который можно интерпретировать как закон Ома для участка цепи с электроемкостью. Здесь
который можно интерпретировать как закон Ома для участка цепи с электроемкостью. Здесь  представляет емкостное сопротивление.
представляет емкостное сопротивление.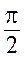 .
. При протекании по катушке переменного тока в ней возникает ЭДС самоиндукции
При протекании по катушке переменного тока в ней возникает ЭДС самоиндукции  Применим II правило Кирхгофа:
Применим II правило Кирхгофа: 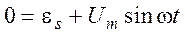 , или
, или 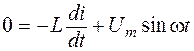 . Из этого выражения следует, что
. Из этого выражения следует, что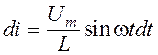 .
.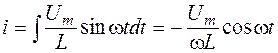 , или
, или  . Следовательно,
. Следовательно, ,
,  .
.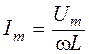 можно записать в виде
можно записать в виде ,
, представляет индуктивное сопротивление.
представляет индуктивное сопротивление.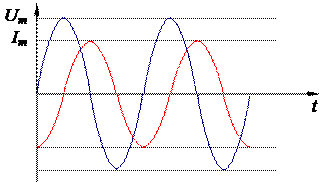 Условие
Условие 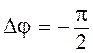 означает, что синусоиды, изображающие зависимости силы тока и напряжения от времени, сдвинуты относительно друг друга на четверть периода, то есть напряжение по фазе опережает ток на
означает, что синусоиды, изображающие зависимости силы тока и напряжения от времени, сдвинуты относительно друг друга на четверть периода, то есть напряжение по фазе опережает ток на  .
.
 .
. ,
,  ,
, 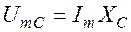 . (1)
. (1) , направим по оси токов. Учитывая, что на индуктивном сопротивлении напряжение опережает ток на
, направим по оси токов. Учитывая, что на индуктивном сопротивлении напряжение опережает ток на  , вектор
, вектор  направим перпендикулярно оси токов вверх (будем считать положительными углы поворота против часовой стрелки). Тогда вектор, изображающий напряжение на емкости
направим перпендикулярно оси токов вверх (будем считать положительными углы поворота против часовой стрелки). Тогда вектор, изображающий напряжение на емкости  , которое отстает от тока на
, которое отстает от тока на 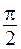 , будет ориентирован противоположно вектору
, будет ориентирован противоположно вектору  . Результатом сложения этих трех векторов будет вектор длиной
. Результатом сложения этих трех векторов будет вектор длиной 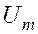 .
. Вначале сложим противоположно направленные векторы
Вначале сложим противоположно направленные векторы  .
. ,
, .
.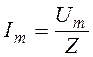 ,
,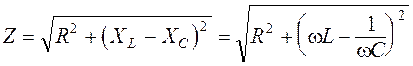
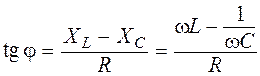 .
. . Из векторной диаграммы видно, что
. Из векторной диаграммы видно, что 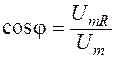 . Применяя закон Ома, получаем, что
. Применяя закон Ома, получаем, что  , или
, или .
.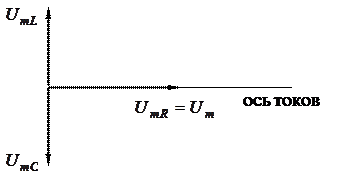 В рассматриваемой цепи ток будет максимальным, если
В рассматриваемой цепи ток будет максимальным, если  , то есть напряжения на индуктивном и емкостном сопротивлениях совпадают по величине:
, то есть напряжения на индуктивном и емкостном сопротивлениях совпадают по величине:  . Это явление называется резонансом напряжений.
. Это явление называется резонансом напряжений. При параллельном соединении напряжения на всех элементах цепи, одинаковы и равны внешнему напряжению, а мгновенные значения токов складываются, то есть
При параллельном соединении напряжения на всех элементах цепи, одинаковы и равны внешнему напряжению, а мгновенные значения токов складываются, то есть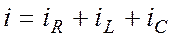 .
. ,
, 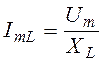 ,
,  . (1)
. (1) , направим по оси напряжений. Учитывая, что на индуктивном сопротивлении напряжение опережает ток на
, направим по оси напряжений. Учитывая, что на индуктивном сопротивлении напряжение опережает ток на 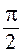 , вектор
, вектор  направим перпендикулярно оси токов вниз. Тогда вектор, изображающий ток на электроемкости
направим перпендикулярно оси токов вниз. Тогда вектор, изображающий ток на электроемкости  , который опережает напряжение на
, который опережает напряжение на  . Результатом сложения этих трех векторов будет вектор длиной
. Результатом сложения этих трех векторов будет вектор длиной  .
. Вначале сложим противоположно направленные векторы
Вначале сложим противоположно направленные векторы 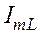 и
и 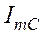 . Затем применим теорему Пифагора, согласно которой
. Затем применим теорему Пифагора, согласно которой .
. ,
, .
. ,
,
 , или, что то же самое,
, или, что то же самое,  полное сопротивление цепи минимально и равно активному сопротивлению: Z = R. Токи на индуктивном и емкостном сопротивлениях совпадают по величине:
полное сопротивление цепи минимально и равно активному сопротивлению: Z = R. Токи на индуктивном и емкостном сопротивлениях совпадают по величине:  , сдвиг фаз между током и напряжением равен нулю. Это явление называется резонансом токов
, сдвиг фаз между током и напряжением равен нулю. Это явление называется резонансом токов Рассмотрим параллельное соединение катушки и конденсатора. При параллельном соединении напряжения на всех элементах цепи, одинаковы и равны внешнему напряжению, а мгновенные значения токов складываются, то есть
Рассмотрим параллельное соединение катушки и конденсатора. При параллельном соединении напряжения на всех элементах цепи, одинаковы и равны внешнему напряжению, а мгновенные значения токов складываются, то есть .
.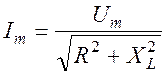 ,
,
 ,
, и
и 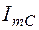 . Сложим эти векторы по правилу параллелограмма. Силу тока в подводящих проводах
. Сложим эти векторы по правилу параллелограмма. Силу тока в подводящих проводах  найдем по теореме косинусов
найдем по теореме косинусов .
.