
|
|
ЛАБОРАТОРНАЯ РАБОТА № 11. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛПервообразной функции f(x) на промежутке X изменения независимой переменной х называется функция F(x), удовлетворяющая равенству F¢(x)=f(x), xÎX. Неопределённым интегралом функции f(x) на промежутке X называется множество всех первообразных F(x) этой функции на заданном промежутке. Для обозначения неопределённого интеграла функции используется символ
Эта формула представляет структуру неопределённого интеграла функции: все первообразные отличаются друг от друга на некоторую постоянную величину C. Одним из наиболее часто применяемых правил при вычислении неопределённых интегралов является правило (или формула) интегрирования по частям:
В этой формуле u и v являются функциями некоторой независимой переменной. В пакете student содержится специальная команда intparts(), реализующая формулу интегрирования по частям. Её использование мы продемонстрируем на примере решения конкретной задачи. Задача 1.Вычислить интеграл Решение. Прежде всего подключим пакет student командой >with(student): Для удобства дальнейших ссылок на вычисляемый интеграл присвоим его с помощью команды Int() переменной Integral: >Integral:=Int(exp(-x)*cos(x/2),x);
Для вычисления интеграла нам придется два раза применить формулу интегрирования по частям. Проинтегрируем по частям исходный интеграл первый раз. Для этого воспользуемся командой intparts(интеграл, u), где первый параметр интеграл является вычисляемым интегралом в виде Int(u*v,x), а второй параметр u представляет функцию u в формуле интегрирования по частям. Чтобы читателю стало яснее, мы записали формулу интегрирования по частям применительно к параметрам команды intparts():
Интегрируем исходный интеграл по частям, выбрав > g:=simplify(intparts(Integral,exp(-x)));
Интегрирование по частям пока не принесло нам желаемого результата. У нас все равно имеется интеграл, который мы не можем тотчас же вычислить, используя таблицу интегралов. Выделим этот интеграл и также применим к нему правило интегрирования по частям: > Integral2:=op(2,g);
> g1:=simplify(intparts(Integral2,exp(-x)));
Видим, что интегрирование по частям интеграла Integral2 привело к выражению, содержащему исходный неопределённый интеграл. Подставим полученное значение интеграла Integral2 в переменную g, представляющую выражение искомого интеграла Integral после первого интегрирования по частям: > g:=subs(Integral2=g1,g);
Подведем итог нашим вычислениям. Дважды проинтегрировав по частям, мы пришли к представлению исходного интеграла Integral через него же самого. Теперь остается только решить уравнение Integral=g относительно неизвестной переменной Integral (в правой части уравнения она содержится неявно) для получения значения искомого интеграла: > Integral:=simplify(solve(Integral=g, Integral));
Проверить полученный ответ можно дифференцированием diff(Integral,x) или вычислением исходного интеграла с помощью команды int(): > simplify(diff(Integral,x));
> simplify(int(exp(-x)*cos(x/2),x));
Обратите внимание на использование команды simplify() на протяжении всего примера. Она упрощает получаемые выражения и представляет их в удобном для пользователя виде. Задание. Вычислить интегралы Задача 2. Вычислить интеграл Решение. Подынтегральная функция является правильной рациональной дробью. Вычисление подобных интегралов осуществляется разложением подынтегральной функции на простейшие дроби. Решение начнем с присваивания выражения подынтегральной функции некоторой переменной (dr). Затем выделим из него знаменатель (переменная dn), который разложим на множители и сохраним в переменной dnf: > dr:=(3*x^2+8)/(x^3+4*x^2+4*x);
> dn:=denom(dr);
Команда denom выделяет знаменатель (denominator) дроби. > dnf:=factor(dn);
Команда factor разлагает на множители. Теперь можем "написать" схему разложения подынтегральной дроби на простейшие, причем для доступа к структурным элементам выражения dnf будем использовать команду op(): > drSimple:=A/op(1,dnf)+B/op(1,op(2,dnf))+C/op(2,dnf);
В выражении drSimple переменные A, B и C представляют собой неопределённые коэффициенты, которые необходимо определить, приравняв это выражение исходной рациональной дроби dr. Для этого мы приводим к общему знаменателю дробь drSimple: > dns1:=simplify(drSimple);
После чего выделяем её числитель (numerator), а также числитель дроби dr: > dns:=numer(dns1);
> drs:=numer(dr);
Выделенные числители должны быть равны между собой, так как знаменатели у дробей dns1 и dr одинаковы. Но чтобы они были равными, необходимо, чтобы коэффициенты при одинаковых степенях независимой переменной x были также равными между собой. Это приводит к системе трёх уравнений относительно трёх неизвестных величин A, B и C в разложении подынтегральной дроби на элементарные дроби. Её решение завершает процедуру разложения правильной подынтегральной рациональной дроби на элементарные слагаемые дроби: > e1:=coeff(dns,x^2)=coeff(drs,x^2);
> e2:=coeff(dns,x)=coeff(drs,x);
> e3:=coeff(dns,x,0)=coeff(drs,x,0);
> solve({e1,e2,e3},{A,B,C});
Теперь можно командой assign() присвоить им полученные из решения системы значения и посмотреть на окончательный вид разложения подынтегральной дроби на элементарные слагаемые дроби: > assign(%); > drSimple;
Так как полученное нами выражение является иным представлением исходного подынтегрального выражения, то, естественно, интеграл от него равен интегралу от этого исходного выражения. Теперь остается только вычислить каждый из интегралов суммы drSimple, чтобы получить окончательный ответ. Но прежде чем переходить к их вычислению, сделаем одно замечание относительно разложения правильной рациональной дроби на простейшие. Мы, собственно говоря, повторили процедуру классического алгоритма разложения дроби на сумму простейших. В Maple можно было бы воспользоваться командой преобразования дроби к типу parfrac (partial fraction – простейшая дробь), который и представляет собой сумму элементарных дробей для заданной дробно-рациональной функции: > convert(dr,parfrac,x);
Вернемся к вычислению нашего интеграла через полученное разложение. Интеграл от первого слагаемого является табличным, но мы его вычислим с использованием команды int(): > In1:=Int(op(1,drSimple),x);
> In1:=value(In1);
Второй интеграл сводится к табличному простой заменой переменной u=x+2. Для автоматизации замены переменных в интеграле можно воспользоваться командой changevar() (change variable – изменить переменную) пакета student, в которой первым параметром в виде уравнения задаётся выражение новой переменной интегрирования через старую, а второй параметр представляет сам интеграл: > In2:=Int(op(2,drSimple),x);
> with(student):changevar(x+2=u,In2);
> In2:=value(%);
Теперь остается только вернуться к старой переменной, используя команду subs()(substitute – заменить): > In2:=subs(u=x+2,In2);
Третий интеграл вычисляется такой же заменой переменной, как и в случае вычисления второго интеграла: > In3:=Int(op(3,drSimple),x);
> In3:=changevar(x+2=u,In3);
> In3:=value(In3);
> In3:=subs(u=x+2,In3);
Теперь остается только "записать" исходный интеграл как сумму трёх вычисленных интегралов (произвольную постоянную мы опускаем): > Integ:=In1+In2+In3;
Проверим полученный результат дифференцированием > simplify(diff(Integ,x));
и интегрированием с помощью команды int() > int((3*x^2+8)/(x^3+4*x^2+4*x),x);
Задание. Вычислить интегралы С помощью языка Maple можно написать собственную процедуру интегрирования по частям выражения f(x)g(x), в котором первая функция f(x) представляет собой полином относительно переменной x, а g(x) – функция некоторого специального вида. Например, когда мы вычисляем интеграл от выражения > collect(int((x^2-x+1)*exp(x),x),exp(x));
Как мы вычисляем вручную подобные интегралы? Прежде всего разбиваем его на сумму интегралов, общий вид каждого слагаемого в которой можно представить в форме:
После этого каждый из интегралов интегрируем по частям до тех пор, пока не получим интеграл, вычисляемый непосредственно. Действительно, проинтегрируем представленный выше общий интеграл по частям:
Мы видим, что в результате получается новый интеграл, но в котором степень переменной x уменьшена на единицу по сравнению с исходным. Повторяя далее эти вычисления по частям для вновь получаемых интегралов, мы дойдем до интеграла от экспоненты, который равен самой экспоненте. Таким образом, вычисление нашего исходного интеграла завершится. При большей степени n нам придется выполнить больше интегрирования по частям, при меньшей меньше, но всегда мы будем завершать вычисления, доходя до интеграла от экспоненты. Эти размышления можно использовать для создания рекурсивной процедуры вычисления рассматриваемого интеграла IntXnExp (степень nonnegint (nonnegative integer) – неотрицательная целая), которая при n=0 завершает рекурсию, возвращая экспоненциальную функцию: > IntXnExp:=proc(n::nonnegint, x::name) if n=0 then return exp(x) else x^n*exp(x)-n*IntXnExp(n-1,x); end if; end proc: Чтобы вычислить, например, интеграл > IntXnExp(4,x);
Задание. Проверить работу процедуры IntXnExp для n=0, 1, 2, 3, 5, 10. Теперь на основе разработанной процедуры интегрирования одного члена полинома, умноженного на экспоненциальную функцию, можно написать процедуру интегрирования произведения полинома любой степени на экспоненциальную функцию: > IntPolynomExp:=proc(p::polynom, x::name) local i, result; result:=add(coeff(p,x,i)*IntXnExp(i,x), i=0..degree(p,x)); collect(result, exp(x)); end proc: В этой процедуре с помощью команды add() вычисляется сумма коэффициентов полинома, умноженных, соответственно, на интеграл > IntPolynomExp((x^3-2)*(x+1),x);
Задания. 1. Объяснить работу процедуры IntPolynomExp. 2. Вычислить интегралы 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , при этом
, при этом
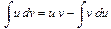 .
. .
.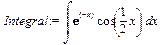
 .
.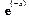 в качестве функции u:
в качестве функции u:

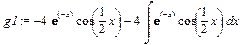

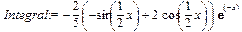
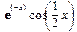
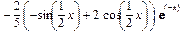
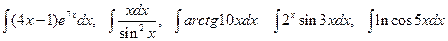 .
.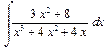 .
.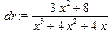


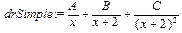
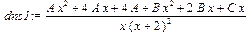

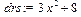
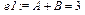

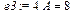
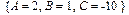

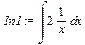

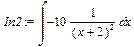
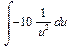
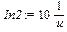
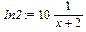
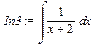



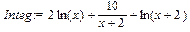
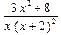
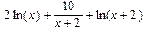
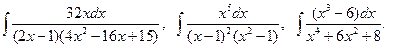
 , то результат также представляется в виде произведения некоторого полинома на ту же самую экспоненциальную функцию:
, то результат также представляется в виде произведения некоторого полинома на ту же самую экспоненциальную функцию: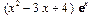


 , можно вызвать разработанную процедуру со следующими параметрами:
, можно вызвать разработанную процедуру со следующими параметрами: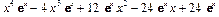
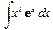 , т. е. строится первообразная полинома, умноженного на экспоненту. Интеграл вычисляется с помощью рекурсивной процедуры IntXnExp(), разработанной нами ранее. Возвращаемое значение представляет собой полином, умноженный на экспоненту, которое получается в результате выполнения команды collect(). Теперь мы можем быстро вычислять интегралы для функций рассмотренного класса с помощью разработанной нами процедуры:
, т. е. строится первообразная полинома, умноженного на экспоненту. Интеграл вычисляется с помощью рекурсивной процедуры IntXnExp(), разработанной нами ранее. Возвращаемое значение представляет собой полином, умноженный на экспоненту, которое получается в результате выполнения команды collect(). Теперь мы можем быстро вычислять интегралы для функций рассмотренного класса с помощью разработанной нами процедуры: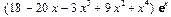
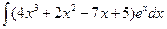 ,
, 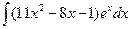 .
.