
|
|
Среднее и действующее значения синусоидально изменяющейся величиныЛекция № 7 Под средним значением синусоидально изменяющейся величины понимают среднее её за полпериода. Так, среднее значение тока: а,
Рис. 2-5. Пояснение смысла среднего значения В выражении (2-8) Если эту площадь равномерно распределить на полпериода, что достигается делением интеграла на T/2, то высота полученного прямоугольника и будет среднее значение. Очень широко применяют понятие действующего значения синусоидально изменяющейся величины. Его называют также эффективным или среднеквадратичным. Из математики известно, что среднеквадратичное значение для синусоидального тока определяется следующим образом:
Получается это так:

Выражение (2-12) подставляется в (2-11) и получается окончательное выражение для действующего значения синусоидального тока. Аналогично
Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока Количество теплоты, выделенное за один период синусоидального тока
Выделенная за то же время постоянным током теплота равна
Приравняем их
или
Таким образом, действующее значение синусоидального тока I численно равно значению такого постоянного тока 2-4. Коэффициент амплитуды и коэффициент формы Коэффициент амплитуды Ка- это отношение амплитуды периодически изменяющейся функции к её действующему значению. Так, для синусоидального тока Ка = Коэффициент формы Кф- это отношение действующего значения периодически изменяющейся функции к её среднему значению за полпериода. Для синусоидального тока Кф = Для несинусоидальных периодических токов Ка 2-5. Изображение синусоидально изменяющихся величин векторами на комплексной плоскости. Комплексная амплитуда. Комплекс действующего значения
Рис. 2-6. Комплексная плоскость. На рис. 2-6 дана комплексная плоскость, на которой можно изобразить комплексные числа. Комплексное число имеет действительную (вещественную) и мнимую части. По оси абсцисс откладывается действительная часть комплексного числа, а по оси ординат – мнимая часть. На оси действительных значений ставят значок +1, а на оси мнимых значений – значок +j (j= Сразу отметим, что далее пригодится: j²= - 1; -j²=1; (2-19) Из курса математики известно формула Эйлера:
Комплексное число
Проекция функции Если вместо функции
Рис. 2-7. Комплексная плоскость На комплексной плоскости функция (2-21) как и функция Угол α в формуле (2-20) может быть любым. Предположим, что Тогда:
Рис. 2-8. Комплексная плоскость Слагаемое
а, функция
Таким образом синусоидально изменяющийся ток i можно представить как мнимую часть вектора С целью единообразия принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для момента времени
где Величину Рассмотрим два примера на переход от мгновенного значения тока к комплексной амплитуде и от комплексной амплитуды к мгновенному значению. Пример 1. Ток Записать выражение комплексной амплитуды этого тока.
Пример 2. Комплексная амплитуда тока Согласно формуле (2-24) записываем
Под комплексом действующего значения тока

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (2-8)
(2-8) (2-9)
(2-9) . (2-10)
. (2-10)
 определяет площадь положительной полуволны синусоиды. На рис.5 эта площадь обозначена косой штриховкой.
определяет площадь положительной полуволны синусоиды. На рис.5 эта площадь обозначена косой штриховкой. (2-11)
(2-11)
 (2-13)
(2-13) ,текущего одинаковое время по одному и тому же сопротивлению.
,текущего одинаковое время по одному и тому же сопротивлению. . (2-14)
. (2-14) (2-15)
(2-15) ,
, (2-16)
(2-16) , который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток. (2-17)
(2-17) (2-18)
(2-18) и Кф
и Кф  . Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального.
. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального.
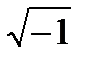 ).
). (2-20)
(2-20) изображают на комплексной плоскости вектором, численно равным единице и составляющим угол α с осью вещественных значений, т.е. с осью +1. Угол α отсчитывается против часовой стрелки от оси +1. Модуль функции
изображают на комплексной плоскости вектором, численно равным единице и составляющим угол α с осью вещественных значений, т.е. с осью +1. Угол α отсчитывается против часовой стрелки от оси +1. Модуль функции 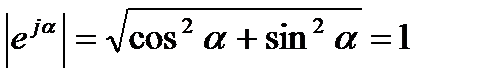
 на ось +1 равна cosα, а на ось +j равна sinα.
на ось +1 равна cosα, а на ось +j равна sinα.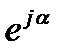 взять функцию
взять функцию  , то
, то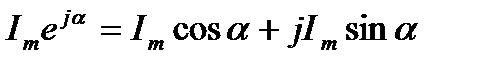 (2-21)
(2-21)
 изобразится вектором под углом α к вещественной оси +1, по величине вектора будет в
изобразится вектором под углом α к вещественной оси +1, по величине вектора будет в  раз больше.
раз больше. , т.е. что угол α изменяется пропорционально времени.
, т.е. что угол α изменяется пропорционально времени. (2-22)
(2-22)
 представляет собой действительную часть (Re) выражения
представляет собой действительную часть (Re) выражения  :
: , (2-23)
, (2-23) представляют собой мнимую часть (Im) выражения
представляют собой мнимую часть (Im) выражения  :
: (2-24)
(2-24) , или, что то же самое, как проекцию вращающегося вектора
, или, что то же самое, как проекцию вращающегося вектора  на мнимую ось +j (рис. 2-8).
на мнимую ось +j (рис. 2-8). . При этом вектор
. При этом вектор  , (2-25)
, (2-25) - комплексная величина; модуль её равен
- комплексная величина; модуль её равен 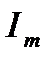 , а угол под которым
, а угол под которым  проведён к оси +1 на комплексной плоскости равен начальной фазе ψ.
проведён к оси +1 на комплексной плоскости равен начальной фазе ψ.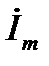 называют комплексной амплитудой тока i . Комплексная амплитуда изображает ток i на комплексной плоскости для момента времени
называют комплексной амплитудой тока i . Комплексная амплитуда изображает ток i на комплексной плоскости для момента времени  .
. .
. Следовательно
Следовательно 
 Записать выражение для мгновенного значения этого тока.
Записать выражение для мгновенного значения этого тока.
 понимают частное от деления комплексной амплитуды тока
понимают частное от деления комплексной амплитуды тока  на
на  :
: