|
Четвертая основная граничная задача фильтрации
Оценка параметра 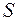 и ОП качества вскрытияпродуктивного пласта и ОП качества вскрытияпродуктивного пласта
(  пласт неоднородный k = var) пласт неоднородный k = var)
В том случае, когда приствольная зона скважины  представляет собой область непрерывного изменения проницаемости представляет собой область непрерывного изменения проницаемости  , уравнение неразрывности (3.57) видоизменится: , уравнение неразрывности (3.57) видоизменится:
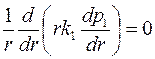 . .
| (3.72)
| Для удаленной части пласта 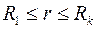 распределение давления распределение давления  соответствует решению (3.51), а для приствольной зоны путем интегрирования (3.56) находим соответствует решению (3.51), а для приствольной зоны путем интегрирования (3.56) находим
 . .
| (3.73)
| Примем закономерность изменения проницаемости в области  в виде в виде
 , ,
|
| где  – проницаемость удаленной части пласта, т. е. при – проницаемость удаленной части пласта, т. е. при 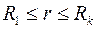
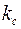 – проницаемость стенки скважины – проницаемость стенки скважины  . .
После подстановки  в (3.73),интегрирования и определения постоянных в (3.73),интегрирования и определения постоянных  из граничных условий (3.68) получим следующее решение задачи: из граничных условий (3.68) получим следующее решение задачи:
где 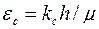 , а расход , а расход 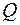 вычисляется по обобщенной формуле Дюпюи (3.65), в которой приведенный радиус скважины надо принять вычисляется по обобщенной формуле Дюпюи (3.65), в которой приведенный радиус скважины надо принять
 . .
|
|
Используя сходство этой формулы с формулой (3.70), легко найти
параметр 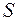 , исходя непосредственно из формулы (3.71): , исходя непосредственно из формулы (3.71):
Пусть, например, при бурении проницаемого интервала 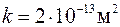
на стенке скважины сформирована глинистая корка проницаемостью  , т. е. , т. е. 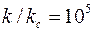 и и  . Принимая . Принимая  и и  , получим , получим
 и и  , ,
т. е. поглощение фильтрата бурового раствора уменьшится более чем в 2 раза.
5. Плоская фильтрация в вертикально-трещиноватом пласте
Если пласт содержит упорядоченную систему трещин, то в нем благодаря анизотропии проницаемости плоско-радиальный характер фильтрации не будет иметь место (см. разд. 2).
Рассмотрим случай, когда одно из главных направлений анизотропии Ox3 совпадает с направлением оси скважины Oz (например, упорядоченная система вертикальных трещин в вертикальной скважине). Тогда два других главных направления анизотропии Ох1 и Ох2 расположены в плоскости  , т. е. параллельно кровле и подошве пласта. При заданных однородных граничных условиях в скважине и на поверхности питания (3.55) фильтрация будет плоской, так как , т. е. параллельно кровле и подошве пласта. При заданных однородных граничных условиях в скважине и на поверхности питания (3.55) фильтрация будет плоской, так как  , но не радиальной. В плоскости х1х2 имеют место обобщенный закон Дарси [см. формулу (2.40)] , но не радиальной. В плоскости х1х2 имеют место обобщенный закон Дарси [см. формулу (2.40)]
 , ,
|
| и соответствующее ему уравнение неразрывности [см. формулу (2.42)]
 . .
| (3.74)
| Как было сказано в разд. 2, введением новой системы координат

| (3.75)
| уравнение (3.74),заданное в анизотропной плоскости х1х2, преобразуется в уравнение Лапласа
 . .
| (3.76)
|
для изотропной плоскости  , проницаемость которой , проницаемость которой
Принимая скважину в качестве источника (или стока) интенсивностью  , получим, аналогично (3.62), поле давления , получим, аналогично (3.62), поле давления
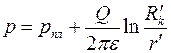 . .
| (3.77)
| где 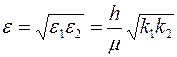 , , 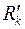 – радиус контура питания в плоскости – радиус контура питания в плоскости  . Отсюда следует, что эквипотенциальной поверхностью . Отсюда следует, что эквипотенциальной поверхностью  являются: окружность являются: окружность  в плоскости в плоскости  и эллипс и эллипс  в плоскости х1х2, где в плоскости х1х2, где  – полуоси эллипса. – полуоси эллипса.
Это означает, что контуром питания (где 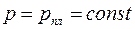 ) в анизотропном пласте может быть только эллипс ) в анизотропном пласте может быть только эллипс

| (3.78)
| Согласно (3.59) этому эллипсу в плоскости  соответствует окружность соответствует окружность  . В то же время окружность . В то же время окружность  преобразуется в эллипс преобразуется в эллипс

| (3.79)
| Поэтому в строгой постановке первая основная граничная задача формулируется так: найти решение уравнения (3.76), удовлетворяющее условию 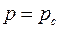 в точках эллипса (3.79) и условию в точках эллипса (3.79) и условию  на окружности на окружности  . .
Однако для определения расхода 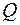 ‚ достаточно хорошее приближение получается, если эллипс (3.79) заменить эквивалентной окружностью радиуса ‚ достаточно хорошее приближение получается, если эллипс (3.79) заменить эквивалентной окружностью радиуса
 . .
| (3.80)
| Используя в (3.61) условие 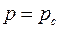 при при  получим получим
 . .
| (3.81)
|
Если истинный эллиптический контур питания (3.78) заменить условным – окружностью радиуса

| (3.82)
|
то, выразив 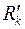 через через  и подставив полученное выражение и соотношение (3.80) в (3.81) придем к обычной формуле Дюпюи (3.65), в которой и подставив полученное выражение и соотношение (3.80) в (3.81) придем к обычной формуле Дюпюи (3.65), в которой  , а приведенный радиус скважины, приведенные коэффициенты гидропроводности и продуктивности надо принять равными: , а приведенный радиус скважины, приведенные коэффициенты гидропроводности и продуктивности надо принять равными:

| (3.83)
| где 
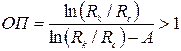 . .
| (3.84)
| Отсюда следует, что при прочих равных условиях в анизотропном пласте расход жидкости выше, чем в изотропном пласте эквивалентной гидропроводности  . .
В нижеследующей таблице приведены значения  при нескольких параметрах анизотропии при нескольких параметрах анизотропии 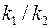 и и  . .
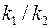
|
|
|
| 102
| 103
| 104
| 
| 1,03
| 1,05
| 1,15
| 1,21
| 1,50
| 2,05
| Видно, что влияние анизотропии заметно при больших отношениях  . .
6. Определение расхода в неоднородном анизотропном пласте
Если после вскрытия пласта проницаемости 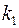 и и  в приствольной зоне скважины изменились и стали равными в приствольной зоне скважины изменились и стали равными  и и  то возникает задача об определении расхода в неоднородном анизотропном пласте. Приближенное решение этой задачи может быть без труда найдено при следующих условиях: то возникает задача об определении расхода в неоднородном анизотропном пласте. Приближенное решение этой задачи может быть без труда найдено при следующих условиях:
главные направления проницаемостей в приствольной зоне и удаленной части пласта совпадают;
границей раздела областями является эллипс
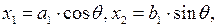
| (3.85)
| где 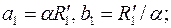  – радиус границы раздела в преобразованной плоскости – радиус границы раздела в преобразованной плоскости  . .
Обозначим давление на общей границе через  и рассмотрим каждую из областей независимо друг от друга. и рассмотрим каждую из областей независимо друг от друга.
Так как подобным эллипсам (3.78) и (3.85) в плоскости  соответствуют концентрические окружности соответствуют концентрические окружности 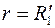 и и  , то для удаленной части пласта имеем [см. формулу (3.81)] , то для удаленной части пласта имеем [см. формулу (3.81)]
 , ,
| (3.86)
|
где  –приведенная гидропроводность удаленной части пласта. Рассматривая приствольную зону скважины, замечаем, что здесь преобразование системы координат х1х2 в –приведенная гидропроводность удаленной части пласта. Рассматривая приствольную зону скважины, замечаем, что здесь преобразование системы координат х1х2 в  осуществляется с помощью другого параметра анизотропии осуществляется с помощью другого параметра анизотропии  ,т. е. ,т. е.
Следовательно, границы этой области: эллипс (3.69) и окружность  преобразуются в эллипсы с соответствующими полуосями преобразуются в эллипсы с соответствующими полуосями
Заменив эти эллипсы эквивалентными окружностями, радиусы которых равны

| (3.87)
| получим приближенную формулу для расхода жидкости
 , ,
| (3.88)
|
где  – приведенная гидропроводность призабойной части пласта. – приведенная гидропроводность призабойной части пласта.
Определив  из равенства правых частей (3.86) и (3.88), после преобразования получим следующую обобщенную формулу Дюпюи: из равенства правых частей (3.86) и (3.88), после преобразования получим следующую обобщенную формулу Дюпюи:
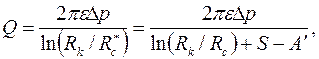 , ,
| (3.89)
| где
 . .
|
| Видно, что при  и и 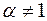 имеем имеем  , т. е. влияние анизотропии исчезает, если призабойная зона скважины в результате кольматации приобрела свойства изотропной среды. Аналогичный результат имеет место при , т. е. влияние анизотропии исчезает, если призабойная зона скважины в результате кольматации приобрела свойства изотропной среды. Аналогичный результат имеет место при  и и  , что возможно, например, при гидроразрыве изотропного пласта. Отсюда следует вывод гидроразрыв гранулярного коллектора в ПЗ не может привести к заметному росту продуктивности скважины. Его положительная роль сводится к разрушению зоны кольматации и тем самым восстановлению потенциальной продуктивности пласта. Только при гидроразрыве анизотропного пласта, когда , что возможно, например, при гидроразрыве изотропного пласта. Отсюда следует вывод гидроразрыв гранулярного коллектора в ПЗ не может привести к заметному росту продуктивности скважины. Его положительная роль сводится к разрушению зоны кольматации и тем самым восстановлению потенциальной продуктивности пласта. Только при гидроразрыве анизотропного пласта, когда  , продуктивность скважины может быть увеличена. , продуктивность скважины может быть увеличена.
7. Несовершенное вскрытие пластов
Фильтрация, отличная от плоско-радиальной, возникает и в том случае, когда пласт вскрыт не на всю мощность, а частично или часть пласта перекрыта обсадной колонной, или связь пластовой и скважинной жидкостей осуществляется через перфорационные отверстия в колонне.
В этих случаях говорят о несовершенном вскрытии пласта и задают граничное условие 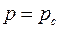 лишь на открытой части поверхности лишь на открытой части поверхности  , а на остальной условие непроницаемости , а на остальной условие непроницаемости  . Течение жидкости в таких условиях вблизи скважины пространственно, и, естественно, решение задачи фильтрации усложняется. . Течение жидкости в таких условиях вблизи скважины пространственно, и, естественно, решение задачи фильтрации усложняется.
Известны различные приближенные аналитические решения этих задач и экспериментальные исследования на моделях, учитывающие тот или иной вид несовершенства вскрытия пласта.
Общий вывод, который следует из полученных решений, сводится к тому, что расход жидкости и в этих случаях вычисляется по обобщенной формуле Дюпюи (3.49), где приведенный радиус скважины
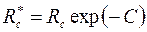 , ,
| (3.90)
| здесь 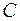 – показатель фильтрационного сопротивления, связанный с несовершенством вскрытия пласта. – показатель фильтрационного сопротивления, связанный с несовершенством вскрытия пласта.
Отношение расхода жидкости 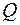 при несовершенном вскрытии к расходу при несовершенном вскрытии к расходу  при совершенном вскрытии пласта в тех же условиях определяют аналогично параметру ОП [см. формулу (3.66)] при совершенном вскрытии пласта в тех же условиях определяют аналогично параметру ОП [см. формулу (3.66)]
коэффициент сопротивления:
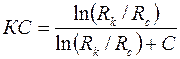 . .
| (3.50)
|
| (3.91)
| В общем случае  где где  и и  – показатели сопротивления, обусловленные несовершенством по степени и характеру вскрытия пласта. Для случая вскрытия части пласта – показатели сопротивления, обусловленные несовершенством по степени и характеру вскрытия пласта. Для случая вскрытия части пласта  Маскет, используя метод источников, нашел, что при Маскет, используя метод источников, нашел, что при  показатель несовершенства по степени вскрытия можно определить по формуле показатель несовершенства по степени вскрытия можно определить по формуле
 . .
| (3.50)
|
| (3.91)
|
Здесь  , ,
где  – гамма-функция (известная, табулированная функция); – гамма-функция (известная, табулированная функция);  . .
Представление о функции  и показателе и показателе  дает табл. 3. дает табл. 3.
Таблица 3
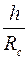
| 
| | 0,9
| 0,8
| 0,7
| 0,6
| 0,5
| 0,4
| 0,3
| 0,2
| 
| | 0,43
| 0,84
| 1,38
| 2,04
| 2,93
| 4,33
| 7,1
| 13,11
| |
| 0,16
| 0,47
| 0,91
| 1,52
| 2,35
| 2,62
| 5,35
| 8,1
| |
| 0,24
| 0,65
| 1,21
| 1,98
| 3,04
| 3,65
| 6,87
| 10,87
| |
| 0,41
| 1,05
| 1,89
| 3,05
| 4,66
| 6,07
| 10,63
| 17,39
| |
| 0,49
| 1,22
| 2,19
| 3,52
| 5,35
| 7,11
| 12,24
| 20,08
|
Например, при Rc = 0,1 м, h = 20 м, h1 = 10 м, согласно таблице при h/Rc=200 и h1=0,5, получим С1=3,35, что при  соответствует коэффициенту сопротивления КС = 0,65. соответствует коэффициенту сопротивления КС = 0,65.
Существенное значение в этой задаче могут иметь различные проницаемости вдоль пласта 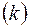 и в направлении, перпендикулярном к пласту и в направлении, перпендикулярном к пласту  , т. е. анизотропия проницаемости. Доказано, что учесть этот фактор можно, если заменить истинную мощность пласта , т. е. анизотропия проницаемости. Доказано, что учесть этот фактор можно, если заменить истинную мощность пласта  приведенной приведенной  . .
Если, например,  , то по данным предыдущего примера имеем , то по данным предыдущего примера имеем 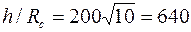 , , 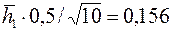 и, согласно формулам, и, согласно формулам,  и и  . .
Несовершенство по характеру вскрытия имеет место, когда связь со скважиной осуществляется через круглые или щелевые отверстия в обсадной колонне. В этом случае показатель несовершенства может быть вычислен по следующим приближенным формулам:

| (3.50)
|
| (3.93)
|
где  – открытая часть поверхности колонны; – открытая часть поверхности колонны;  – диаметры перфорационных отверстий и скважины; т — число рядов щелей. – диаметры перфорационных отверстий и скважины; т — число рядов щелей.

Рис. 3.5 Схема призабойной зоны скважины с искусственным фильтром

Рис. 3.6 Зависимость показателя снижения фильтрационного сопротивления от величины дополнительной зоны фильтрации при h/Re = 15: 1 2, 3 соответственно при Rф/Rc = 8; 5; 3.

Рис. 3.7Зависимость показателя снижения фильтрационного сопротивления от мощности пласта и радиуса фильтра приl/Rф = 2: 1, 2, 3 соответственно
при Rф/Rc = 8; 5; 3
Приведем решение задачи, когда приствольная зона скважины оборудована искусственным фильтром (2)высотой  и проницаемостью и проницаемостью  , отличной от проницаемости пласта (1)(рис. 3.5). , отличной от проницаемости пласта (1)(рис. 3.5).
Приведенный радиус в этом случае
 , ,
| (3.94)
| где 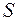 – параметр «скин-эффекта» [см. формулу (3.71)]; – параметр «скин-эффекта» [см. формулу (3.71)];  показатель снижения сопротивления, обусловленный наличием дополнительной зоны показатель снижения сопротивления, обусловленный наличием дополнительной зоны  ; φ – функция безразмерных параметров ; φ – функция безразмерных параметров  , ,  , ,  . .
На рис. 3.6 показаны графики зависимости φ от  при трех значениях отношения при трех значениях отношения  и и  . Из него следует, что с увеличением . Из него следует, что с увеличением  функция функция  быстро растет до асимптотического значения, которое наступает при быстро растет до асимптотического значения, которое наступает при 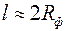 . Это доказывает нецелесообразность установки фильтра высотой больше чем . Это доказывает нецелесообразность установки фильтра высотой больше чем  . .
Влияние мощности пласта на φиллюстрируется графиками на рис.3.7 при тех же значениях  и и 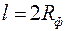 . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 и ОП качества вскрытияпродуктивного пласта
и ОП качества вскрытияпродуктивного пласта пласт неоднородный k = var)
пласт неоднородный k = var) представляет собой область непрерывного изменения проницаемости
представляет собой область непрерывного изменения проницаемости  , уравнение неразрывности (3.57) видоизменится:
, уравнение неразрывности (3.57) видоизменится: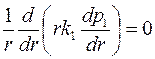 .
.
 распределение давления
распределение давления  соответствует решению (3.51), а для приствольной зоны путем интегрирования (3.56) находим
соответствует решению (3.51), а для приствольной зоны путем интегрирования (3.56) находим .
.
 ,
,
 – проницаемость удаленной части пласта, т. е. при
– проницаемость удаленной части пласта, т. е. при 
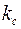 – проницаемость стенки скважины
– проницаемость стенки скважины  .
.  в (3.73),интегрирования и определения постоянных
в (3.73),интегрирования и определения постоянных  из граничных условий (3.68) получим следующее решение задачи:
из граничных условий (3.68) получим следующее решение задачи:
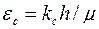 , а расход
, а расход 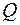 вычисляется по обобщенной формуле Дюпюи (3.65), в которой приведенный радиус скважины надо принять
вычисляется по обобщенной формуле Дюпюи (3.65), в которой приведенный радиус скважины надо принять .
.

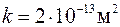
 , т. е.
, т. е. 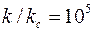 и
и  . Принимая
. Принимая  и
и  , получим
, получим и
и  ,
,  , т. е. параллельно кровле и подошве пласта. При заданных однородных граничных условиях в скважине и на поверхности питания (3.55) фильтрация будет плоской, так как
, т. е. параллельно кровле и подошве пласта. При заданных однородных граничных условиях в скважине и на поверхности питания (3.55) фильтрация будет плоской, так как  , но не радиальной. В плоскости х1х2 имеют место обобщенный закон Дарси [см. формулу (2.40)]
, но не радиальной. В плоскости х1х2 имеют место обобщенный закон Дарси [см. формулу (2.40)] ,
,
 .
.

 .
.
 , проницаемость которой
, проницаемость которой
 , получим, аналогично (3.62), поле давления
, получим, аналогично (3.62), поле давления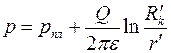 .
.
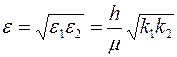 ,
,  – радиус контура питания в плоскости
– радиус контура питания в плоскости  являются: окружность
являются: окружность  в плоскости
в плоскости  в плоскости х1х2, где
в плоскости х1х2, где  – полуоси эллипса.
– полуоси эллипса.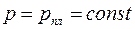 ) в анизотропном пласте может быть только эллипс
) в анизотропном пласте может быть только эллипс
 . В то же время окружность
. В то же время окружность 
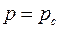 в точках эллипса (3.79) и условию
в точках эллипса (3.79) и условию  на окружности
на окружности  .
. .
.
 получим
получим .
.

 и подставив полученное выражение и соотношение (3.80) в (3.81) придем к обычной формуле Дюпюи (3.65), в которой
и подставив полученное выражение и соотношение (3.80) в (3.81) придем к обычной формуле Дюпюи (3.65), в которой  , а приведенный радиус скважины, приведенные коэффициенты гидропроводности и продуктивности надо принять равными:
, а приведенный радиус скважины, приведенные коэффициенты гидропроводности и продуктивности надо принять равными:

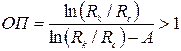 .
.
 при нескольких параметрах анизотропии
при нескольких параметрах анизотропии  и
и  .
. .
.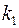 и
и  в приствольной зоне скважины изменились и стали равными
в приствольной зоне скважины изменились и стали равными  и
и  то возникает задача об определении расхода в неоднородном анизотропном пласте. Приближенное решение этой задачи может быть без труда найдено при следующих условиях:
то возникает задача об определении расхода в неоднородном анизотропном пласте. Приближенное решение этой задачи может быть без труда найдено при следующих условиях:
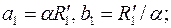
 – радиус границы раздела в преобразованной плоскости
– радиус границы раздела в преобразованной плоскости  и рассмотрим каждую из областей независимо друг от друга.
и рассмотрим каждую из областей независимо друг от друга.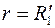 и
и  ,
,
 ,т. е.
,т. е.


 ,
,
 – приведенная гидропроводность призабойной части пласта.
– приведенная гидропроводность призабойной части пласта.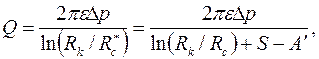 ,
,
 .
.
 и
и 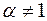 имеем
имеем  , т. е. влияние анизотропии исчезает, если призабойная зона скважины в результате кольматации приобрела свойства изотропной среды. Аналогичный результат имеет место при
, т. е. влияние анизотропии исчезает, если призабойная зона скважины в результате кольматации приобрела свойства изотропной среды. Аналогичный результат имеет место при  и
и  , что возможно, например, при гидроразрыве изотропного пласта. Отсюда следует вывод гидроразрыв гранулярного коллектора в ПЗ не может привести к заметному росту продуктивности скважины. Его положительная роль сводится к разрушению зоны кольматации и тем самым восстановлению потенциальной продуктивности пласта. Только при гидроразрыве анизотропного пласта, когда
, что возможно, например, при гидроразрыве изотропного пласта. Отсюда следует вывод гидроразрыв гранулярного коллектора в ПЗ не может привести к заметному росту продуктивности скважины. Его положительная роль сводится к разрушению зоны кольматации и тем самым восстановлению потенциальной продуктивности пласта. Только при гидроразрыве анизотропного пласта, когда  , продуктивность скважины может быть увеличена.
, продуктивность скважины может быть увеличена. . Течение жидкости в таких условиях вблизи скважины пространственно, и, естественно, решение задачи фильтрации усложняется.
. Течение жидкости в таких условиях вблизи скважины пространственно, и, естественно, решение задачи фильтрации усложняется.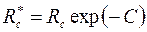 ,
,
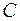 – показатель фильтрационного сопротивления, связанный с несовершенством вскрытия пласта.
– показатель фильтрационного сопротивления, связанный с несовершенством вскрытия пласта. при совершенном вскрытии пласта в тех же условиях определяют аналогично параметру ОП [см. формулу (3.66)]
при совершенном вскрытии пласта в тех же условиях определяют аналогично параметру ОП [см. формулу (3.66)]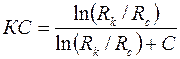 .
.
 где
где  и
и  – показатели сопротивления, обусловленные несовершенством по степени и характеру вскрытия пласта. Для случая вскрытия части пласта
– показатели сопротивления, обусловленные несовершенством по степени и характеру вскрытия пласта. Для случая вскрытия части пласта  Маскет, используя метод источников, нашел, что при
Маскет, используя метод источников, нашел, что при  показатель несовершенства по степени вскрытия можно определить по формуле
показатель несовершенства по степени вскрытия можно определить по формуле .
.
 ,
, – гамма-функция (известная, табулированная функция);
– гамма-функция (известная, табулированная функция);  .
. и показателе
и показателе  дает табл. 3.
дает табл. 3.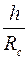


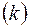 и в направлении, перпендикулярном к пласту
и в направлении, перпендикулярном к пласту  , т. е. анизотропия проницаемости. Доказано, что учесть этот фактор можно, если заменить истинную мощность пласта
, т. е. анизотропия проницаемости. Доказано, что учесть этот фактор можно, если заменить истинную мощность пласта  приведенной
приведенной  .
. , то по данным предыдущего примера имеем
, то по данным предыдущего примера имеем 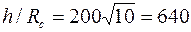 ,
, 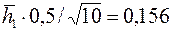 и, согласно формулам,
и, согласно формулам,  и
и  .
.
 – открытая часть поверхности колонны;
– открытая часть поверхности колонны;  – диаметры перфорационных отверстий и скважины; т — число рядов щелей.
– диаметры перфорационных отверстий и скважины; т — число рядов щелей.


 и проницаемостью
и проницаемостью  , отличной от проницаемости пласта (1)(рис. 3.5).
, отличной от проницаемости пласта (1)(рис. 3.5). ,
,
 показатель снижения сопротивления, обусловленный наличием дополнительной зоны
показатель снижения сопротивления, обусловленный наличием дополнительной зоны  ; φ – функция безразмерных параметров
; φ – функция безразмерных параметров  ,
,  ,
,  .
. . Из него следует, что с увеличением
. Из него следует, что с увеличением  быстро растет до асимптотического значения, которое наступает при
быстро растет до асимптотического значения, которое наступает при 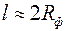 . Это доказывает нецелесообразность установки фильтра высотой больше чем
. Это доказывает нецелесообразность установки фильтра высотой больше чем  .
.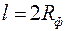 .
.