
|
|
ФЕРРОМАГНЕТИКИ В ПЕРЕМЕННЫХ МАГНИТНЫХ ПОЛЯХ12
5.2.1. На рис. 61 изображена динамическая петля гистерезиса тороидального магнитного сердечника, полученная на частоте 1 МГц. Путем графических построений с последующим расчетом найти тангенс угла магнитных потерь и добротность сердечника. Определить активную мощность, выделяющуюся в сердечнике, используемом в катушке индуктивностью L=10 мГн, если по обмотке катушки проходит ток I=1 мА частотой 1 МГц. Получите выражение для комплексной магнитной проницаемости материала сердечника, полагая, что его эффективная магнитная проницаемость на частоте 1 МГц равна 200.
Решение На высоких частотах изменения индукции в ферромагнетике отстают от изменения напряженности магнитного поля на угол δм который называется углом магнитных потерь. Этот угол определяется длиной отрезка аа' (рис. 62) на зависимости Н=Нтsinωt, где точка а соответствует моменту времени, когда Н=0, а точка а' — моменту, когда В=0. Из рис. 62 следует, что δм≈π/8 и tgδм=0,414. Добротность сердечника Qм=(tgδм)-1=2,41.
Активная мощность, выделяющаяся в сердечнике,
Pа=I2ωLtgδм=(10-3)2·2π·106·10·10-3·0,414=2,6·10-2 Вт.
Комплексная магнитная проницаемость Примечание. Угол магнитных потерь может быть найден и другим способом. Из определения δм следует, что
Н=Нт sinωt; В=Вт sin (ωt-δм).
При ωt-π/2 (точка в на рис. 62)
Н=Нт; В=Вт sin(π/2-δм)=Втcosδм=B1.
При ωt=π/2+δм (точка г на рис. 62) В=Вт. Отсюда cosδм=B1/Bm. Взяв значения B1 и Вт из рис. 62 (в относительных единицах), получаем cosδм=0,92; δм=23°≈π/8. 5.2.2*. В слабых магнитных полях петля гистерезиса приближенно описывается эмпирической формулой Рэлея:
где знак минус соответствует интервалу возрастания H, а знак плюс — интервалу уменьшения H. Пользуясь этой формулой, построить петлю гистерезиса и определить потери на гистерезис в кольцевом магнитном сердечнике с площадью поперечного сечения S=25 мм2 и средней длиной магнитного контура lср=50 мм при воздействии на него переменного магнитного поля частотой 50 Гц и амплитудой напряженности Hm=20 А/м. Начальная магнитная проницаемость материала сердечника μн=1000, эмпирическая постоянная β=200 м/А.
Решение Подстановка исходных данных в формулу Рэлея приводит к зависимостям: при возрастании H
В=1,26·10-4H2+6,3·10-3H — 5,03·10-2; при уменьшении Я
B=-1,26·10-4H2+6,3·10-3H + 5,03·10-2.
Результаты расчетов петли гистерезиса по приведенным формулам показаны на рис. 63.
Потери на гистерезис за один цикл перемагничивания, отнесенные к единице объема сердечника, определяются площадью статической петли:
где В↓ соответствует уменьшению H, B↑ — возрастанию H. На частоте 50 Гц потери на вихревые токи не играют существенной роли, поэтому петлю на рис. 63 можно рассматривать как статическую. Активная мощность, выделяющаяся в сердечнике за счет потерь на гистерезис при циклическом перемагничивании полем частотой 50 Гц,
5.2.3*. При испытании магнитного сердечника на частоте f=1 кГц с помощью установки, схема которой представлена на рис. 64, были получены следующие результаты: UG=300 мВ, Ur=30 мВ. Вычислить магнитную проницаемость, индукцию и напряженность магнитного поля в кольцевом сердечнике размерами R×r×h=30×20×10 мм, если число витков измерительной обмотки п=30, а сопротивление резистора, ограничивающего ток в измерительном контуре, R0=10 Ом.
Решение По измеренному значению падения напряжения на резисторе
Пренебрегая активным сопротивлением обмотки и потерями в магнитном сердечнике, находим падение напряжения на катушке индуктивности:
Индуктивность катушки с исследуемым сердечником
Учитывая, что потокосцепление Ψ=nBS=LI, где S — площадь поперечного сечения сердечника, находим индукцию магнитного поля в сердечнике
При известном токе в обмотке напряженность магнитного поля в кольцевом сердечнике
где
5.2.4. На кольцевой ферритовый сердечник размерами
5.2.5. На рис. 65 изображены основная кривая (штриховая) намагничивания и предельная петля гистерезиса, которые получены для тороидального магнитного сердечника с двумя изолированными намагничивающими обмотками. Как в этом случае можно получить частные петли гистерезиса I и II (заштрихованные области на рис. 65)?
5.2.6. Пользуясь рис. 65, определить реверсивную магнитную проницаемость материала для случая, когда перемагничивание осуществляется по частной петле гистерезиса I. 5.2.7*. Докажите, что потери на перемагничивание, отнесенные к единице объема материала сердечника (удельные потери), могут быть вычислены по формуле pм=Pа/V=μ0μωH2tgδм.
Решение На рис. 66 представлены эквивалентная схема и векторная диаграмма катушки индуктивности с магнитным сердечником. Пренебрегая активным сопротивлением обмотки, для активной мощности, выделяющейся в катушке индуктивности из-за потерь, в сердечнике, получаем Pa=rмI2=I2ωLtgδм.
При заданном токе в обмотке напряженность магнитного поля в кольцевом сердечнике Н=Iп/lср, где lср — средняя длина магнитного контура в сердечнике. Индуктивность катушки определяется выражением L=μ0μn2S/lср, где μ — магнитная проницаемость кольцевого сердечника. Окончательно имеем
где V=lсрS — объем магнитного сердечника.
5.2.8. Всердечнике трансформатора удельные магнитные потери на гистерезис и на вихревые токи при частоте 2 кГц равны и составляют 2 Вт/кг. Определить суммарные удельные магнитные потери в сердечнике на частоте 400 Гц, если максимальная магнитная индукция в нем та же, что и на частоте 2 кГц. 5.2.9. В сердечнике трансформатора суммарные удельные магнитные потери на гистерезис и на вихревые токи при частотах 1 и 2 кГц составляют соответственно 2 и 6 Вт/кг (при неизменной максимальной индукции в сердечнике). Рассчитать магнитные потери на вихревые токи в сердечнике на частоте 2 кГц.
Решение Суммарные потери за один цикл перемагничивания линейно зависят от частоты:
где η, n и ξ — коэффициенты, зависящие от свойств материала и формы сердечника. Подставляя исходные данные, запишем для двух частот:
Вычитая из одного уравнения другое, получаем 5.2.10. Укажите, какими способами можно полностью размагнитить ранее намагниченный ферромагнитный образец. 5.2.11. На рис. 67 изображены основная кривая (штриховая) намагничивания магнитного материала и петли гистерезиса для двух значений амплитуды напряженности переменного магнитного поля (
Рис. 67
5.2.12. В сердечнике трансформатора на частоте 50 Гц потери на гистерезис при индукции магнитного поля 0,1 и 0,5 Тл составляют 0,15 и 1,97 Вт/кг соответственно. Определить потери на гистерезис на частоте 200 Гц при индукции магнитного поля 0,6 Тл.
Решение Потери на гистерезис в единице объема ферромагнетика определяются выражением
Поскольку коэффициенты n и η не зависят от частоты и магнитной индукции, искомые потери Рг3=0,12·(0,6)1,6·200=10,6 Вт/кг.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , где μ'=μ; μ"=μtgδм, т. е.
, где μ'=μ; μ"=μtgδм, т. е.  .
. ,
,





 определяем ток в измерительном контуре:
определяем ток в измерительном контуре:
 .
. Гн.
Гн. Тл.
Тл.
 — средняя длина магнитного контура в сердечнике. Тогда относительная магнитная проницаемость материала сердечника
— средняя длина магнитного контура в сердечнике. Тогда относительная магнитная проницаемость материала сердечника .
.
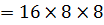 мм, изготовленный из материала марки 2000 НН, нанесена измерительная обмотка, содержащая десять витков. Определить, каким должно быть напряжение UG, чтобы ток в измерительной схеме (см. рис. 64) при испытаниях на частоте 1 МГц составлял 10 мА. Сопротивление образцового резистора R0=47 Ом.
мм, изготовленный из материала марки 2000 НН, нанесена измерительная обмотка, содержащая десять витков. Определить, каким должно быть напряжение UG, чтобы ток в измерительной схеме (см. рис. 64) при испытаниях на частоте 1 МГц составлял 10 мА. Сопротивление образцового резистора R0=47 Ом.


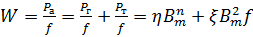 ,
,
 .
. . Тогда
. Тогда  .
. ). Полагая, что напряженность магнитного поля меняется по синусоидальному закону, изобразите форму кривой, характеризующей изменение магнитной индукции во времени для каждого из двух значений
). Полагая, что напряженность магнитного поля меняется по синусоидальному закону, изобразите форму кривой, характеризующей изменение магнитной индукции во времени для каждого из двух значений  . При
. При  укажите на кривой мгновенные значения магнитной индукции для моментов времени, когда мгновенные значения напряженности магнитного поля равны нулю.
укажите на кривой мгновенные значения магнитной индукции для моментов времени, когда мгновенные значения напряженности магнитного поля равны нулю.
 . Отсюда следует, что
. Отсюда следует, что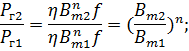

 Дж/(кг·Тл1,6).
Дж/(кг·Тл1,6).