
|
|
Краткие теоретические сведения12 НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ «ВТУ»
Утверждаю ____________________ Первый проректор _____________________ «____»_________ 2012 г.
Кафедра «Автоматизации и управления»
Методические указания для выполнения практических занятий по курсу:
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
направление подготовки 220400.62 – Управление в технических системах
форма обучения: заочная
Оренбург, 2012 Составитель: Кулешов И.В., к.т.н., доцент
УДК 547(07) ББК 24.477 О64
Рецензент:
Теория автоматического управления: методические указания по выполнению практических занятий / сост. И. В. Кулешов. – Оренбург: НОУ ВПО МТИ «ВТУ», 2012. – 25 с.
Методические указания предназначены для студентов заочной формы обучения к практическим занятиям по дисциплине «Теория автоматического управления»по направлению подготовки 220400.62 – Управление в технических системах Рассмотрено на заседании кафедры «Автоматизации и управления» и рекомендовано к изданию (протокол №___, от «___»_______2012 г.) ББК 24.477 О64 ©Кулешов И.В. ©МТИ «ВТУ», 2012
Содержание
Введение………………………………………………………………………… 4 1. Практическое занятие № 1: «Линеаризация дифференциальных уравнений состояния системы автоматического управления» -– 2 часа …………… 5 1.1. Цель занятия……………………………………………………………….. 5 1.2. Краткие теоретические сведения………………………………………….. 5 1.3. Пример решения…………………………………………………………… 5 1.4. Задания……………………………………………………………………… 6 1.5. Контрольные вопросы…………………………………………………….. 11 2. Практическое занятие № 2: «Преобразование Лапласа. Передаточная функция. Расположение корней уравнения на комплексной плоскости.» – 4 часа…………………………………………………………………………..11 2.1. Цель занятия………………………………………………………………...11 2.2. Краткие теоретические сведения…………………………………………..11 2.3. Пример решения……………………………………………………………12 2.4. Задания………………………………………………………………………13 2.5. Контрольные вопросы……………………………………………………...17 3. Практическое занятие № 3: «Критерии устойчивости САУ» – 4 часа…………………………………………………………..………………17 3.1. Цель занятия………………………………………………………………...17 3.2. Краткие теоретические сведения………………………………………….17 3.3. Пример решения……………………………………………………………18 3.4. Задания………………………………………………………………………19 3.5. Контрольные вопросы……………………………………………...………22
Список рекомендуемой литературы……………………………………...……22 Приложения…………………………………………………………………….. 24
Введение
Практические занятия по дисциплине «Теория автоматического управления» проводятся в компьютерном классе МТИ для студентов заочного обучения, по направлению подготовки 220400.62 – Управление в технических системах. Программой дисциплины предусмотрено 10 часов практических занятий по трем темам. Цельюпрактического курса дисциплины «Теория автоматического управления» является формирование у студентов знаний общих принципов построения и законов функционирования систем автоматического и организационного управления, основных методов анализа и синтеза систем, эффективно функционирующих при детерминированных и случайных воздействиях. Задачи практического курса дисциплины состоят в следующем: Сформировать базовые практические навыки, лежащие в основе теории автоматического управления. Сформировать представления и знания о фундаментальных принципах синтеза идеальной структуры и оптимизации параметров систем управления Научить синтезировать законы и алгоритмы оптимального управления объектами. Научить анализу систем автоматического управления. Сформировать представления и знания о моделировании систем автоматического управления
В результате выполнения практических занятий студент должен: знать: - основные принципы управления - методы и математический аппарат описания и моделирования объектов и систем управления - методы оценки точности, устойчивости и качества систем управления - фундаментальные принципы синтеза идеальной структуры и оптимизации параметров систем управления - основные проблемы и перспективные направления развития теории управления
уметь: - использовать методы анализа устойчивости и качества систем управления - обоснованно выбирать структурные схемы регулирования и управления, рассчитывать оптимальные настройки регуляторов - синтезировать законы и алгоритмы оптимального управления объектами - применять ЭВМ для исследования систем управления и для управления технологическими объектами
владеть: - навыками практического применения анализа устойчивости и качества систем управления - навыками применения ЭВМ для исследования систем управления и для управления технологическими объектами - методами описания и моделирования объектов и систем управления
Практическое занятие № 1: «Линеаризация дифференциальных уравнений состояния системы автоматического управления» Цель занятия Получить практические навыки линеаризации уравнения статики и динамики в окрестностях номинальных режимов. Краткие теоретические сведения
Линеаризация – процесс приведения криволинейных статических характеристик звеньев, используемых в процессе управления к прямолинейным характеристикам. Самым распространенным методом, используемым в процессе линеаризации, является метод малых отклонений, который допускает, что отклонения входных и выходных параметров системы в процессе управления от их установившихся значений достаточно малы. В основе метода линеаризации лежит разложение в ряд Тейлора, которое позволяет разложить нелинейную функцию нескольких переменных по степеням малых отклонений этих переменных в окрестностях значений, соответствующих заданному установившемуся режиму.
Пример решения.
Линеаризация нелинейного дифференциального уравнения (ДУ). 3xy - 4x2 + 1,5 Данное ДУ является нелинейным из-за наличия произведений переменных х и у. Линеаризируем его в окрестности точки с координатами х0 = 1, 3у0 - 4 + 0 = 0 + у0 откуда у0 = 2. Введем в рассмотрение функцию F = 3xy - 4x2 + 1,5x’y - 5y’ - y и определим все ее производные при заданных начальных условиях:
Теперь, используя полученные коэффициенты, можно записать окончательное линейное ДУ: -5.Dy’ + 2.Dy + 3.Dх’ - 2.Dх = 0.
Линеаризация ДУ, заданного в явном виде относительно у, т.е. y = F(x) производится по формуле
то есть, в данном случае нет необходимости искать производные по у. Задание: (решение задач)
Линеаризовать уравнения статики и динамики в окрестностях номинальных режимов.
Варианты заданий:
Вариант № 1 1. Линеаризовать уравнение статики в окрестности номинального режима xн = 2
2. Линеаризовать уравнение динамики в окрестности номинального режима xн = 2 и определить передаточную функцию звена y(2) + y . y(1) + y3 = 2 . x2. Вариант № 2 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 2.х2 + x5
2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена
uн = fн = 0, yн = 2. Вариант № 3 1. Линеаризовать уравнение статики в окрестности номинального режима
uн = 0,5; fн = 1 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(2) + 2 . y . y(1) + y = 2 . u(1) . f + u3, uн = 1, fн = 2. Вариант № 4 1. Линеаризовать уравнение статики в окрестности номинального режима
uн = 1; fн = 2. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(2) + y . y(1) + y3 = u(1) . f + u . f + u2, uн = 1, fн = 2. Вариант № 5
2 . u . uн = 2; fн = 1. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(1) + y + y . u - 2 . u . f + u(1) = 0, uн = 0,5, fн = 1. Вариант № 6 1. Линеаризовать уравнение статики в окрестности номинального режима xн = 1
y(1) + y = 2 . u . f + u (1), uн = 0,5; fн = 2. Вариант № 7 1. Линеаризовать уравнение статики в окрестности номинального режима
y2 - 2.u.x - x3 - 4 = 0. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(2) + y . y(1) + y2 = 2 . x. Вариант № 8 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 4.х2 + x3. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена
uн = 2; fн = 1. Вариант № 9 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 2.х2 + x.
y(1) . (2 + y) + y = u2 . u(1) + f, uн = 0,5; fн = 1. Вариант № 10 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 2.х.(1 + x2). 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(2) + y . y(1) + y = 2 . x3 + x . x(1). Вариант № 11 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 2.х.(3 + x) 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y . y(1) + y = 2 . x3 + x . x(1). Вариант № 12 1. Линеаризовать уравнение статики в окрестности номинального режима
uн = 2; fн = 1. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(1) + y + u - u . f + u(1) = 0, uн = 1; fн = 1. Вариант № 13 1. Линеаризовать уравнение статики в окрестности номинального режима
y2 - y . x2 - 2 . x = 0. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(1) + y . y(1) = 2 . x - 8 . x3; xн = 2; yн = 2. Вариант № 14 1. Линеаризовать уравнение статики в окрестности номинального режима
uн = -2; fн = 1.
2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(1) + y(1) . y2 + y = u . u(1) + f . f(1) , uн = 1; fн = 2. Вариант № 15 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 3.х2 + 2.x3. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена
uн = 2; fн = 1. Вариант № 16 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 5.х2 + 3.x. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена
uн = 1; fн = 1. Вариант № 17 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 2.х.(1 + x2). 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(2) + 2.y . y(1) + y = x3 + 3.x . x(1). Вариант № 18 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 2.х.(10 + x). 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена 5.y . y(1) + y = 2 . x3 + 3.x . x(1). Вариант № 19
u . uн = 1; fн = 2. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(1) + y + u - 2.u . f + u(1) = 0, uн = 0.5; fн = 1. Вариант № 20 1. Линеаризовать уравнение статики в окрестности номинального режима
y2 - 4.y . x2 - x = 0. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(1) + y . y(1) = 3 . x - 5 . x3; xн = 2; yн = 1. Вариант № 21 1. Линеаризовать уравнение статики в окрестности номинального режима
uн = 2; fн = 2. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(1) + y(1) . y2 + y = u . u(1) + f . f(1) , uн = 1; fн = 1. Вариант № 22 1. Линеаризовать уравнение статики в окрестности номинального режима
uн = -2; fн = -1.
2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена y(1) + y(1) . y2 + y = u . u(1) + f . f(1) , uн = 1; fн = 1. Вариант № 23 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 2.х2 + 2.x3. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена
uн = 2; fн = 2. Вариант № 24 1. Линеаризовать уравнение статики в окрестности номинального режима
y = 2.х2 + 3.x. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена
uн = 1; fн = 2.
1.5. Контрольные вопросы:
1. Общая форма записи дифференциальных уравнений САУ. 2. Дать описание уравнений статики. 3. Определение и методы линеаризации уравнений. 4. Графическое представление линеаризации уравнений. 5. Стандартная форма записи линейных дифференциальных уравнений. 6. Дать описание уравнений состояния.
2. Практическое занятие № 2: «Преобразование Лапласа. Передаточная функция. Расположение корней уравнения на комплексной плоскости.» – 2 часа
2.1. Цель занятия:
Получение практических навыков использования преобразования Лапласа, определения передаточных функций звеньев САУ, нахождения комплексных корней уравнения состояния.
Краткие теоретические сведения
В теории автоматического управления часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператораp = d/dt так, что, dy/dt = py, а pn = dn/dtn. Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p. В теории автоматического управления широко применяется операторный метод описания линейных систем автоматического управления, использующий интегральное преобразование Лапласа (L – преобразование) Данное преобразование называется прямым односторонним преобразованием Лапласа, преобразует функцию времени х(t) – оригинал, в функцию комплексной переменной X (р) - изображение. Передаточной функцией называется отношение величины выходного параметра, к величине входного параметра, преобразованных по Лапласу, при нулевых начальных условиях.
Пример решения
а) Дано дифференциальное уравнение, характеризующее динамику технологического объекта,
Если обозначить Y(s), X(s) и U(s) как изображения сигналов y, x и u соответственно, то операторное уравнение (при нулевых начальных условиях) в данном случае примет вид: 6,25s2Y(s) + 4sY(s) + Y(s) = 9X(s) – 1,2sX(s) - 5sU(s). Данное уравнение можно преобразовать, вынеся Y(s) и X(s) за скобки: Y(s). (6,25s2 + 4s + 1) = X(s). (9 – 1,2s) - 5sU(s). Отсюда получено:
Если обозначить передаточные функции объекта как
то получается уравнение Y(s) = Wx(s).X(s) + Wu(s).U(s). Структурная схема объекта приведена на рисунке 1.
Полученные передаточные функции имеют одинаковые знаменатели, называемые характеристическими выражениями: A(s) = 6,25s2 + 4s + 1.
Распределение корней на комплексной плоскости показано на рис. 2. По рисунку видно, что корни лежат в левой полуплоскости, следовательно, объект устойчив.
б) Дана передаточная функция вида
Для записи дифференциального уравнения необходимо учесть, что по определению
Y(s) (s – 0,5)(3s2 + 2) = X(s) (7s3 + 5,5), Y(s) (3s3 + 2s – 1,5s2 – 1) = X(s) (7s + 5,5), 3s3 Y(s) + 2s Y(s) – 1,5s2 Y(s) – Y(s) = 7s X(s) + 5,5 X(s).
Теперь, если применить обратное преобразование Лапласа, получается:
2.4. Задания:
а) По заданным дифференциальным уравнениям определить операторные уравнения при нулевых начальных условиях, передаточные функции, структурные схемы звеньев, характеристические уравнения и их корни. Показать распределение корней на комплексной плоскости. Оценить устойчивость каждого из звеньев. б) По заданной передаточной функции записать дифференциальное уравнение.
Вариант № 1 а) б)
Вариант № 2 а) б)
Вариант № 3 а) б)
Вариант № 4 а) б)
Вариант № 5 а) б)
Вариант № 6 а) б)
Вариант № 7 а) б) Вариант № 8 а) б)
Вариант № 9 а) б)
Вариант № 10 а) б)
Вариант № 11 а) б)
Вариант № 12 а) б)
Вариант № 13 а) б)
Вариант № 14 а) б)
Вариант № 15 а) б)
Вариант № 16 а) б)
Вариант № 17 а) б)
Вариант № 18 а) б) Вариант № 19 а) б)
Вариант № 20 а) б)
Вариант № 21 а) б)
Вариант № 22 а) б)
Вариант № 23 а) б)
Вариант № 24 а) б)
2.5. Контрольные вопросы
1. Операторные методы исследования САУ. 2. Преобразование Лапласа. 3. Основные свойства преобразования Лапласа. 4. Передаточная функция САУ. 5. Корневые критерии устойчивости САУ. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 y = 5
y = 5  + y
+ y = 0,
= 0,  = 0. Для определения недостающего начального условия у0 подставим данные значения в ДУ:
= 0. Для определения недостающего начального условия у0 подставим данные значения в ДУ: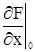 = (3у - 8х
= (3у - 8х  = 3*2 - 8*1 = -2,
= 3*2 - 8*1 = -2, = (3х + 1,5x’ - 1
= (3х + 1,5x’ - 1  = (1,5у
= (1,5у  = -5.
= -5. ,
, y = 2.х + x3
y = 2.х + x3 xн = 1
xн = 1 y(2) + y . y(1) = 2 . u . f + f,
y(2) + y . y(1) = 2 . u . f + f, y = 2 . u2 . f + f3 + 2 . u2
y = 2 . u2 . f + f3 + 2 . u2 y = u . f + u2
y = u . f + u2 1. Линеаризовать уравнение статики в окрестности номинального режима
1. Линеаризовать уравнение статики в окрестности номинального режима - f = 0
- f = 0 y2 + y.х2 - 2. x = 0.
y2 + y.х2 - 2. x = 0. 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена
2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена xн = 1
xн = 1 y(1) . (1 + y) + y = u . u(1) + f . f(1),
y(1) . (1 + y) + y = u . u(1) + f . f(1), xн = 2
xн = 2 2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена
2. Линеаризовать уравнение динамики в окрестности номинального режима и определить передаточную функцию звена xн = 2
xн = 2 u .
u .  xн = 1
xн = 1 xн = 2
xн = 2 y(1) . (1 + 2.y) + y = u . u(1) +. f . f(1),
y(1) . (1 + 2.y) + y = u . u(1) +. f . f(1), xн = 1
xн = 1 1. Линеаризовать уравнение статики в окрестности номинального режима
1. Линеаризовать уравнение статики в окрестности номинального режима 2 .
2 .  .
. .
. ,
,
 и
и  .
.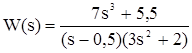 .
. , откуда получено:
, откуда получено: ,
,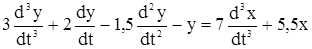 .
.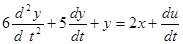 ; y(0) = 1; y’(0) = 2;
; y(0) = 1; y’(0) = 2;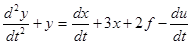 ; y(0) = 10; y’(0) = 6.
; y(0) = 10; y’(0) = 6. .
. ; y(0) = -2; y’(0) = 0;
; y(0) = -2; y’(0) = 0; ; y(0) = -1; y’(0) = 2; y’’(0) = 1.
; y(0) = -1; y’(0) = 2; y’’(0) = 1. .
. ; y(0) = 3; y’(0) = 1;
; y(0) = 3; y’(0) = 1; ; y(0) = 2; y’(0) = -18.
; y(0) = 2; y’(0) = -18. .
. ; y(0) = -1; y’(0) = 2;
; y(0) = -1; y’(0) = 2; ; y(0) = 15; y’(0) = -2.
; y(0) = 15; y’(0) = -2. .
. ; y(0) = 3; y’(0) = -11;
; y(0) = 3; y’(0) = -11; ; y(0) = 1; y’(0) = 2; y’’(0) = -1.
; y(0) = 1; y’(0) = 2; y’’(0) = -1. .
. ; y(0) = 0; y’(0) = -10; y’’(0) = 1.
; y(0) = 0; y’(0) = -10; y’’(0) = 1. .
. ; y(0) = 1; y’(0) = 7;
; y(0) = 1; y’(0) = 7; ; y(0) = -3; y’(0) = 5.
; y(0) = -3; y’(0) = 5. 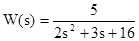 .
.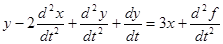 ; y(0) = -1; y’(0) = 4;
; y(0) = -1; y’(0) = 4; ; y(0) = 9; y’(0) = -4.
; y(0) = 9; y’(0) = -4. .
. ; y(0) = -2; y’(0) = 3; y’’(0) = 1;
; y(0) = -2; y’(0) = 3; y’’(0) = 1; ; y(0) = 0.5; y’(0) = 1.
; y(0) = 0.5; y’(0) = 1. .
. ; y(0) = y’’(0) = 10; y’(0) = 1;
; y(0) = y’’(0) = 10; y’(0) = 1; ; y(0) = 9; y’(0) = -1.
; y(0) = 9; y’(0) = -1. .
. ; y(0) = 0; y’(0) = -1; y’’(0) = 1;
; y(0) = 0; y’(0) = -1; y’’(0) = 1; ; y(0) = 1; y’(0) = 0; y’’(0) = 12.
; y(0) = 1; y’(0) = 0; y’’(0) = 12. .
.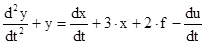 ; y(0) = 5; y’(0) = 3;
; y(0) = 5; y’(0) = 3; ; y(0) = -2; y’(0) = 1.
; y(0) = -2; y’(0) = 1. .
. ; y(0) = -2; y’(0) = 2.
; y(0) = -2; y’(0) = 2. ; y(0) = 7; y’(0) = -2;
; y(0) = 7; y’(0) = -2; ; y(0) = 5; y’(0) = -1.
; y(0) = 5; y’(0) = -1. .
. ; y(0) = 1; y’(0) = 2; y’’(0) = -3;
; y(0) = 1; y’(0) = 2; y’’(0) = -3; ; y(0) = 2; y’(0) = -1; y’’(0) = 1.
; y(0) = 2; y’(0) = -1; y’’(0) = 1. .
. ; y(0) = 1; y’(0) = 2;
; y(0) = 1; y’(0) = 2; ; y(0) = -1; y’(0) = 4.
; y(0) = -1; y’(0) = 4. .
.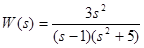 .
. .
. ; y(0) = -2; y’(0) = 4.
; y(0) = -2; y’(0) = 4.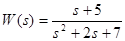 .
. .
. .
. .
.