
|
|
Пример ручного счета в обычной формулировке.Лекция-3 ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ Итерационные методы решения систем линейных Алгебраических уравнений Понятие об итерационных методах решения СЛАУ. В отличие от прямых методов, итерационные методы обычно не дают точного ответа за конечное число шагов, однако на каждом шаге уменьшают ошибку на какую-то долю. Итерации прекращают, когда ошибка становится меньше допуска, заданного вычислителем (пользователем). Величина финальной ошибки зависит от количества итераций, а также от свойств метода и СЛАУ. Другими словам, итерационные методы дают решение СЛАУ в виде предела последовательности некоторых векторов, построение которых осуществляется посредством единообразного процесса, называемого итерационным процессом. Рассмотрим два простейших итерационных метода решения СЛАУ – метод простой итерации и метод Зейделя. Пусть требуется решить СЛАУ
Итерационные методы решения системы уравнений (2.3.1) состоят в построении последовательности векторов
по некоторому алгоритму, такому, что из
где Вычисления ведутся до тех пор, пока норма разницы двух последовательных приближений не станет
где e – малое положительное число (заданная точность). С точностью до e решение принимается равным
Метод Зейделя и метод простой итерации. Пусть задана система уравнений:
Выразим
Полученная запись СЛАУ приводит к двум итерационным процессам.
Метод простой итерации.
Метод Зейделя.
При этом Процесс ведется до выполнения условия Норму
Разница методов состоит в том, что в методе простой итерации новые значения
При решении итерационными методами встает вопрос сходимости получаемых приближений к решению задачи. Достаточный условие сходимости обоих методов состоит в выполнении условия диагонального преобладания:
где, по крайней мере, одно неравенство является строгим (
Матричная формулировка метода простой итерации и метода Зейделя. Представим матрицу
где
Тогда простая итерация имеет вид
Тогда
Аналогично можно представить метод Зейделя в виде
Умножим правую и левую часть равенства на матрицу
или где
из этого следует
Тогда
Пример ручного счета в обычной формулировке. Дана система уравнений
Выполним проверку выполнения достаточного условия сходимости. Проверяем условие диагонального преобладания. первое уравнение: 4>1+1=2 – выполняется; второе уравнение: 2<1+5=6 – не выполняется; третье уравнение: |–1|<1+6=7 – не выполняется. Таким образом, условие диагонального преобладания для исходной системы уравнений не выполняется и поэтому не может быть гарантирована сходимость итерационных методов к решению. Для данной системы можно добиться выполнения этого условия перестановкой второго и третьего уравнений:
Проверяем условие диагонального преобладания для преобразованной системы: первое уравнение: 4>1+1=2 – выполняется; второе уравнение: 6>1+|–1|=2 – выполняется; третье уравнение: 5>1+2=3 – выполняется. Для определения точности приближения воспользуемся нормой вектора
Решение СЛАУ методом простой итерации. Схема пересчета в данном случае имеет вид:
Начальное приближение: Первый шаг итерации (
Второй шаг итерации (
Третий шаг итерации (
После трех итерационных шагов получаем приближенное решение СЛАУ:
Решение СЛАУ методом Зейделя. Схема пересчета в данном случае имеет вид:
Начальное приближение: Первый шаг итерации (
Второй шаг итерации (
При том, что точное решение данной СЛАУ:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (2.3.1)
(2.3.1)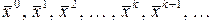 (2.3.2)
(2.3.2) следует
следует  . При этом
. При этом (2.3.3)
(2.3.3) – точное решение системы, а
– точное решение системы, а  – называется начальным приближением решения.
– называется начальным приближением решения. , (2.3.4)
, (2.3.4) .
. . (2.3.5)
. (2.3.5) через остальные члены i-го уравнения:
через остальные члены i-го уравнения: . (2.3.6)
. (2.3.6) ,
,  . (2.3.7)
. (2.3.7) ,
,  (2.3.8)
(2.3.8) задается (
задается (  – номер итерации.
– номер итерации. .
. вектора
вектора  можно, в частности, вычислять по формулам:
можно, в частности, вычислять по формулам: – норма по модулю;
– норма по модулю; – «евклидова» норма;
– «евклидова» норма;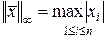 – максимум модуля для элементов вектора.
– максимум модуля для элементов вектора. , а в методе Зейделя они учитываются сразу же после вычисления их для каждого
, а в методе Зейделя они учитываются сразу же после вычисления их для каждого  ,
,  , (2.3.9)
, (2.3.9) ).
). в виде
в виде , (2.3.10)
, (2.3.10) – нижняя треугольная матрица:
– нижняя треугольная матрица: ;
;  (2.3.11)
(2.3.11) – верхняя треугольная матрица:
– верхняя треугольная матрица: ;
;  (2.3.12)
(2.3.12) – диагональная матрица:
– диагональная матрица: ;
;  (2.3.13)
(2.3.13) – сумма верхней и нижней треугольных матриц:
– сумма верхней и нижней треугольных матриц: . (2.3.14)
. (2.3.14) (2.3.15)
(2.3.15)

 (2.3.16)
(2.3.16) (2.3.17)
(2.3.17) в левую часть равенства, т.е.
в левую часть равенства, т.е.
 ,
, – нижняя треугольная матрица с главной диагональю:
– нижняя треугольная матрица с главной диагональю: ;
;  (2.3.18)
(2.3.18) , (2.3.19)
, (2.3.19)

 (2.3.20)
(2.3.20)


 .
. ):
):
 .
. ):
):
 .
. ):
):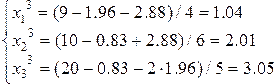

 .
.

 .
.
 Третий шаг итерации (
Третий шаг итерации ( 
 После трех итерационных шагов получаем приближенное решение СЛАУ:
После трех итерационных шагов получаем приближенное решение СЛАУ:  .
. , – отметим большую точность решения. полученного методом Зейделя по сравнению с методом простой итерации за одинаковое количество итерационных шагов.
, – отметим большую точность решения. полученного методом Зейделя по сравнению с методом простой итерации за одинаковое количество итерационных шагов.