
|
|
Асимптотическая формула Пуассона.Предельные теоремы в схеме Бернулли.
Предположим, что мы хотим определить вероятность выпадения ровно 5100 «гербов» при 10000 бросаний монеты. Ясно, что при таком большом числе испытаний использование формулы Бернулли весьма затруднительно с точки зрения вычислений. В таких случаях пользуются асимптотическими формулами Пуассона и Муавра-Лапласа.
Асимптотические формулы Муавра-Лапласа. Теорема 1. Локальная теорема Муавра-Лапласа.Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, а число независимых испытаний п достаточно велико, то вероятностьPn(k) того, что событие А появиться в n испытаниях ровно k раз приближенно равна
где Имеются специальные таблицы, в которых помещены значения функции Пример 1.Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2. Решение. По условию, n = 400; k = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа:
Вычислим х:
Формула Бернулли приводит примерно к такому же результату:
Пример 2.Вероятность поражения мишени стрелком при одном выстреле р = 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз. Решение. По условию, n =10; k = 8; р = 0,75; q = 0,25. Воспользуемся асимптотической формулой Лапласа:
Вычислим х:
Формула Бернулли приводит к иному результату, а, именно Теорема 2. Интегральная теорема Муавра-Лапласа.Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля, и единицы, а число независимых испытаний п достаточно велико, то вероятность Рп (kl, k2) того, что событие А появится в п испытаниях от k1 до k2 раз (не менее k1 и не более k2), приближенно равна определенному интегралу где При решении задач, требующих применения интегральной теоремы Муавра-Лапласа, пользуются специальными таблицами, так как неопределенный интеграл Для того чтобы можно было пользоваться таблицей функции Лапласа, преобразуем соотношение (2) так: Итак,вероятность того, что событие А появится в п независимых испытанияхот k1до k2раз, где Пример.Вероятность того, что деталь не прошла проверку ОТК, равна р = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей. Решение. По условию, р = 0,2; q = 0,8; n = 400; k1= 70; k2=100. Воспользуемся интегральной теоремой Лапласа. Вычислим нижний и верхний пределы интегрирования: Таким образом, имеем Р400(70, 100)=Ф(2,5) - Ф(- 1,25) = Ф(2,5) + Ф(1,25). По таблице находим: Ф (2,5) = 0,4938; Ф( 1,25) = 0,3944. Искомая вероятность Р400(70, 100)=0,4938 + 0,3944=0,8882. Замечание.С помощью функции Лапласа можно найти вероятность отклонения относительной частоты Асимптотическая формула Пуассона.
Пусть число испытаний п в схеме Бернулли неограниченно увеличивается, а вероятность успеха р в одном испытании неограниченно уменьшается, причем их произведение
Замечание 1. Имеются специальные таблицы, пользуясь которыми можно найти Рп(k), зная Замечание 2. Формулу Пуассона применяют, когда вероятность Замечание 3. Формула Пуассона справедлива также по отношению к числу неудач, если число испытаний п в схеме Бернулли неограниченно увеличивается, а вероятность неудачи q в одном испытании неограниченно уменьшается причем Пример. Завод отправил на базу 5000 доброкачественных изделий Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия. Решение. По условию, п = 5000, р = 0,0002, k = 3. По формуле Пуассона искомая вероятность приближенно равна
Формула Пуассона находит широкое применение в теории массового обслуживания. Ее можно считать математической моделью простейшего потока событий. Определение 1. Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Примерами потоков служат: поступление вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов элементов и многие другие. События, образующие поток, в общем случае могут быть различными, но мы будем рассматривать только поток однородных событий, различающихся только моментами появления. Такой поток можно изобразить как последовательность точек Определение 2. Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени. Определение 3. Стационарным называется поток событий, который характеризуется тем, что вероятность появления k событий на промежутке времени длительностью Определение 4. Поток событий называется потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие. Определение 5. Поток событий называется ординарным, если вероятность попадания на бесконечно малый участок Определение 6. Простейшим (стационарным пуассоновским) называют поток событий, который обладает свойствами стационарности, отсутствия последействия и ординарности. Замечание. Установлено что если поток представляет собой сумму очень большого числа независимых стационарных потоков, влияние каждого из которых на всю сумму (суммарный поток) ничтожно мало, то суммарный поток (при условии его ординарности) близок к простейшему.. Можно доказать, что если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за время длительностью t определяется формулой Пуассона.
Эта формула отражает все свойства простейшего потока. Пример. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятности того, что за 5 мин поступит: а) 2 вызова; б) менее двух вызовов; в) не менее двух вызовов. Поток вызовов предполагается простейшим. Решение. По условию А) Б) События не поступило ни одного вызова и поступил один вызов несовместны, поэтому по формуле сложения искомая вероятность
В) События поступило менее 2 вызовов и поступило не менее 2 вызовов противоположны, поэтому

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
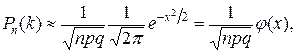 (1)
(1)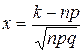 . Причем это равенство тем точнее, чем больше n.
. Причем это равенство тем точнее, чем больше n.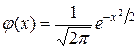 (функция Гаусса), соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция
(функция Гаусса), соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция 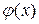 четна, т. е.
четна, т. е.  . При
. При 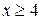
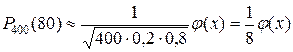
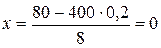 . По таблице находим
. По таблице находим  = 0,3989. Искомая вероятность
= 0,3989. Искомая вероятность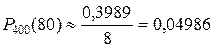 .
.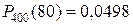 .
.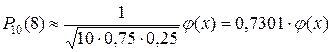 .
. . По таблице находим
. По таблице находим  = 0,3739. Искомая вероятность
= 0,3739. Искомая вероятность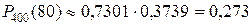 .
.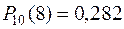 . Столь значительное расхождение ответов объясняется тем, что в настоящем примере п имеет малое значение (формула Муавра-Лапласа дает достаточно хорошие приближения лишь при достаточно больших значениях п).
. Столь значительное расхождение ответов объясняется тем, что в настоящем примере п имеет малое значение (формула Муавра-Лапласа дает достаточно хорошие приближения лишь при достаточно больших значениях п).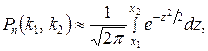 (2)
(2)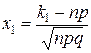 и
и 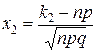 . Причем это равенство тем точнее, чем больше n.
. Причем это равенство тем точнее, чем больше n.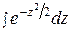 не выражается через элементарные функции. В таблице даны значения функции Лапласа
не выражается через элементарные функции. В таблице даны значения функции Лапласа 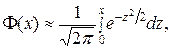 дляположительных значений х и для х = 0; для х < 0 пользуются той же таблицей, функция Ф (x) нечетна, т.е.
дляположительных значений х и для х = 0; для х < 0 пользуются той же таблицей, функция Ф (x) нечетна, т.е. 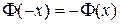 . В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф(х) = 0,5.
. В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф(х) = 0,5.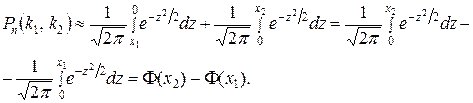
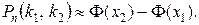

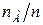 от вероятности р в п независимых испытаниях, используя формулу:
от вероятности р в п независимых испытаниях, используя формулу:  , где
, где 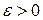 - некоторое число.
- некоторое число.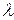 = пр. сохраняет постоянное значение. Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях п, остается неизменным. Тогда Рп(k) определяется по приближенной формуле (формула Пуассона)
= пр. сохраняет постоянное значение. Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях п, остается неизменным. Тогда Рп(k) определяется по приближенной формуле (формула Пуассона)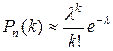 .
.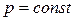 успеха крайне мала, т.е. сам по себе успех является редким событием (например, выигрыш автомобиля по лотерейному билету), но количество испытаний велико, среднее число успехов
успеха крайне мала, т.е. сам по себе успех является редким событием (например, выигрыш автомобиля по лотерейному билету), но количество испытаний велико, среднее число успехов 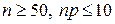 ).
).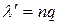 сохраняет постоянное значение.
сохраняет постоянное значение.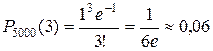 .
.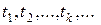 на числовой оси
на числовой оси 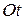 .
.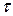 зависит только от числа k и от длительности
зависит только от числа k и от длительности 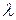 ) есть величина постоянная.
) есть величина постоянная.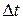 двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.(события появляются не группами, а по одиночке)
двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.(события появляются не группами, а по одиночке)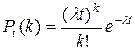
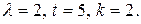 Воспользуемся формулой Пуассона.
Воспользуемся формулой Пуассона.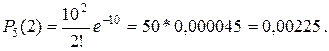
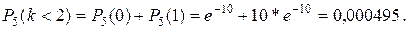 .
.