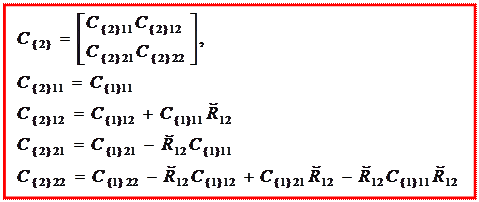|
|
Матрицы и простейшие операции над матрицамиЛекция 1. ЖЕСТКОСТНЫЕ ХАРАКТЕРИСТИКИ УПРУГИХ ЭЛЕМЕНТОВ КОНСТРУКЦИИ Прочность– способность конструкции выдерживать заданную нагрузку, не разрушаясь. Жесткость– способность конструкции препятствовать изменению формы под действием нагрузки.
Рассмотрим жесткостные характеристики прямолинейного стержня.
Приложим в полюсе систему сил
моментов Обозначим:
перемещение полюса (т.О);
Заметим, что положительным направлением для моментов и углов поворота является направление против часовой стрелки.
где
Введем следующие обозначения: Обобщенное перемещение:
.
Обобщенная сила:
.
Запишем перемещение полюса для общего случая формы стержня:
Перепишем уравнения перемещения полюса в координатной форме в следующем виде:
Мы можем записать их в матричной форме:
где
Элемент матрицы податливости
Интеграл Мора, описывающий перемещение
На основании интеграла Мора и выражения (1.5) запишем формулу для определения элементов
Согласно выражения (1.6) является очевидным, что
Лекция 2
Вернемся к выражению (1.4):
Умножим левую и правую части выражения (2.1) на
Тогда,обозначив
где
Здесь
где В рассматриваемом случае
1. Рассмотрим случай, когда i = 1.
2. Рассмотрим случай, когда і = 2
3.Расмотрим случай, когда і = 3:
4.Рассмотрим случай, когда і = 4:
5.Рассмотрим случай, когда і = 5:
6. Рассмотрим случай, когда і = 6:
Тогда согласно формуле (1.6) получаем:
Рассмотрим матрицу податливости прямолинейного упругого элемента, имеющего переменное по длине сечение. Упругий элемент состоит из двух участков: М и Э.
Рассматриваем матрицу податливости в системе координат Oxyz.
Лекция 3. Рассмотрим некоторые свойства четных и нечетных функций. 1) Если А(х)-четная функция, т. е. А(х)=А(-х) (например А(х)=х2), то 2) Если А(х)- нечетная функция, т.е. А(х)=-А(-х) (например А(х)=х), то Если расположить полюс посередине (
Значит, если прямолинейный стержень имеет постоянное сечение по длине стержня, а полюс расположен посередине и при этом жестко связан с незакрепленным концом стержня, то матрица податливости имеет диагональную форму. В случае диагональной матрицы податливости имеем перемещение полюса только в направлении действия силы.
Для упругих элементов постоянного сечения в случае расположения полюса в точке, совпадающей с центром недеформированного стержня, получаем:
В системе нормальных координат при действии в полюсе обобщенной силы, перемещение происходит только в направлении действия силы
Пример: Определим элементы матрицы податливости УЭ постоянного сечения в системе координат, относительно осей и центра которой УЭ обладает симметрией.
Для данного УЭ матрица податливости будет иметь диагональную форму.
Для диагональной матрицы жесткости
Обозначим элементы диагональной матрицы жесткости
Лекция 4. Матрицы и простейшие операции над матрицами
Матрицейразмера В случае равенства строк и столбцов (m=n) матрица носит название квадратной матрицы (
В случае, когда
Матрица размера Матрица размера ( Суммой матриц А+В= С является матрица С, элементы которой определяются по закону Если в любой матрице строки и столбцы поменять местами, то получим транспонированную матрицу При перемножении двух матриц С=А*В необходимо, чтобы количество столбцов матрицы А совпадало с количеством строк матрицы B ( Свойства матричных операций:
Если где
Расчет матрицы податливости упругого элемента в новой базовой системе координат. В зависимости от выбора системы координат (СК) матрицы податливости и жесткости будут изменять не только численные значения своих элементов, но и структуру. Относительное положение любых двух прямоугольных систем координат характеризуется линейным смещением начал координат и угловым смещением осей координат.
Рассмотрим переход из исходной СК (
В матричной форме вектор
Отметим, что
Например, в данном рассматриваемом случае:
Лекция 5. Рассматривается общий случай относительного смещения начал координат двух СК (
Поместим в нижнем индексе {i} номер системы координат, в которой матрица определяется, тогда уравнение равновесия будет иметь вид
Здесь
При этом
Так как
то векторное выражение (5.2) можно записать в следующем матричном виде:
где
Заметим далее, что
Распишем в блочном виде уравнение равновесия (5.1):
Выражения (5.5), (5.6) – уравнения равновесия, записанные в первой и второй (исходной и последующей ) системе координат. Подставим выражения (5.3), (5.4) в уравнение равновесия (5.5):
Приведем эти уравнения к стандартному виду. Запишем сначала первое уравнение в виде:
Подставляем P{2} из первого уравнения в правую часть второго уравнения и переносим соответствующие слагаемые в левую часть второго уравнения:
Сравнивая коэффициенты при обобщенных перемещениях в полученной системе (5.7) и в исходной системе (5.6), приходим к окончательным формулам расчета матрицы жесткости в новой системе координат со смещенным началом координат:
Аналогично получаем формулы для расчета матричных блоков матрицы податливости в случае смещения начала координат:
Лекция 6. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
, а также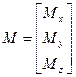
..
–поступательное
– угловое перемещение полюса (т.О).
; 
;
;
; 
;
, (1.1)
- модуль упругости I-го рода (модуль Юнга);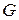
- модуль упругости II-го рода (модуль упругости при сдвиге);
- площадь плоского сечения;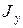
, 
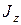- моменты инерции плоских сечений относительно осей Oy, Oz;
- момент инерции при кручении;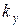
, 
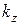- коэффициенты формы при сдвиге;
;
;
;
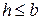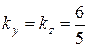( для прямоугольного сечения);
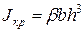(при 
; при 
)
; 
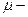коэффициент Пуассона.
;
;
;
;
;
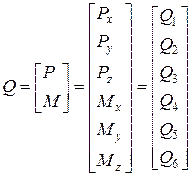
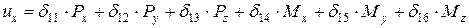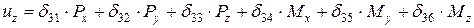. (1.2)
(1.3)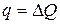
; (1.4)
; 
,
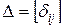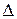- матрица податливости (квадратная матрица размерности (6х6);
( 
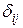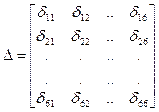Матрица податливости Δ однозначно и полностью описывает жесткостные характеристики рассматриваемого упругого элемента (в данном случае стержня).
-ом направлении при действии единичной силы в 
-ом направлении:
. (1.5)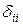
- диагональные элементы характеризуют податливость стержня в направлении действующей силы 
;
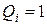- эти элементы характеризуют линейную податливость стержня (размерность элементов [м/Н] );
- эти элементы характеризуют угловую податливость стержня (размерность элементов [1/мН] );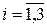
, 
и при 
, 
- эти элементы характеризуют перекрестные связи между угловыми и линейными перемещениями полюса (размерность элементов [1/Н] ).
( 
) произвольной точки 
упругого стержня при действии внешней нагрузки,
где 
- соответствующие внутренние усилия, возникающие от действия внешней нагрузки;
( 
) матрицы податливости:
. (1.6)
( 
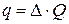. (2.1)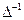
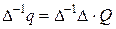. (2.2)
матрицу жесткости, получим уравнение равновесия в матричном виде
, (2.3)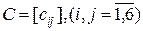
; 
.
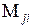- минор матрицы 
Пример расчета матрицы податливости прямолинейного стержня: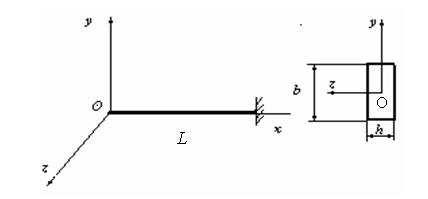
.
; 
.
.
; 
; 
;
; 
;
; 
; 
.
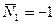
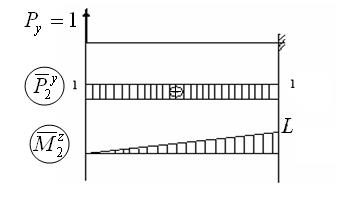
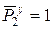
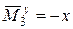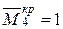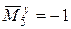
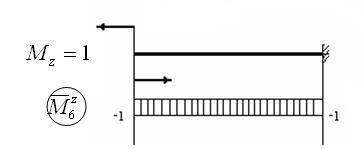
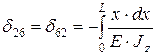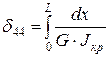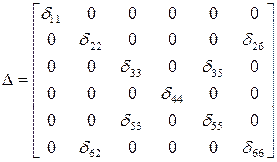
- площадь поперечного сечения инерционной массы;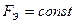
- площадь поперечного сечения упругого элемента;
;
;
; 
;
; 
; 
; 
.
.
.
; 
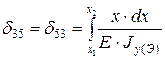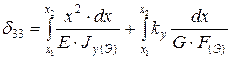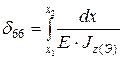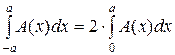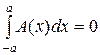) стержня, тогда, используя свойство нечетной функции, можем записать
; 
.
; 
;
; 
; 
;
; 
.
.
; 
; 
; 
,
; 
; 
;
; 
; 
;
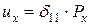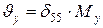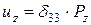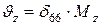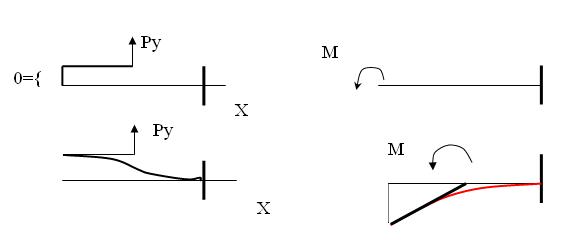
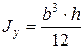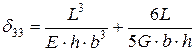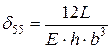- матрица жесткости
.
;
; 
; 
;
; 
; 
.
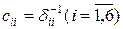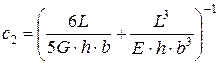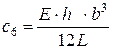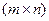называется упорядоченный массив чисел, состоящий из m строк и n столбцов.
).
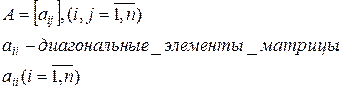
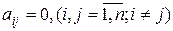, такая матрица называется диагональной.
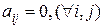- такая матрица называется нулевой.
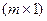называется вектор- столбец.
) называется вектор- строка .
.
.
).
.
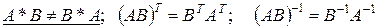, то 
,
.
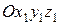) в новую СК ( 
) со смещенным началом координат:
имеет вид:
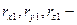проекции вектора на оси первой СК.
.
, 
.
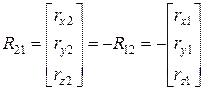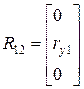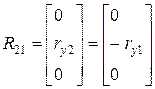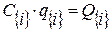. (5.1)
- матрица жесткости (матрица коэффициентов из уравнения равновесия (5.1));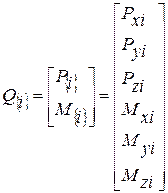
; 
.
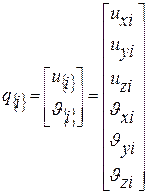(5.2)
;
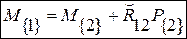; (5.3)
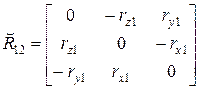- кососимметричная матрица;
.
; 
; 
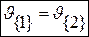. (5.4)
;
(5.5)
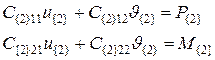(5.6)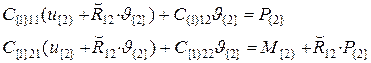
.
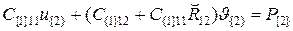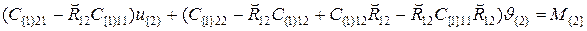. (5.7)
