
|
|
Оценка значимости параметрического коэффициента корреляции.12 Проверка коэффициента корреляции на достоверность осуществляется по критерию Стьюдента. Н0: ρ=0,следовательно R[X,Y] не достоверен (то есть коэффициент корреляции генеральной совокупности ρ=0, следовательно зависимости между XиY нет).
для n<30
В таблице критерия Стьюдента по заданному уровню значимости α и числу степеней свободы: n-2 находим если если Если коэффициент корреляции достоверен, то можно переходить к построению линий регрессии и записать уравнение регрессии.
Построение линий регрессии. Коэффициент корреляции R[X,Y] указывает лишь на наличие связи двух величин, но не даёт возможности судить, как количественно изменяется одна величина относительно другой. Ответ на этот вопрос даёт регрессионный анализ. Корреляционная зависимость характеризуется двумя линиями регрессии:
b=tg α -- угловой коэффициент. Если R[X,Y] ≠1,то условные средние y̅I не лягут на одну прямую, но при R[X,Y] ≈1 (R=0,95, R=0,85) можно провести усредняющую прямую. Так как имеем две линии регрессии:
то для y=y̅(x):
то для x=x̅(y):
σ(Y)=Sn(Y) выборочные оценки среднего σ(X)=Sn(X) квадратического отклонения. Так как обе линии регрессии проходят через точку с координатами (x̅,y̅), где x̅,y̅ -- общие средние, вычисленные по выборке, то уравнение регрессии имеет вид:
или:
6. Ранговый коэффициент корреляции.
Определить, есть ли связь между признаками XиY, можно и с помощью рангового коэффициента корреляции. Он менее точен и не может использоваться для построения линий регрессии, но так как ранговый коэффициент корреляции легко вычислить, есть смысл воспользоваться им для первоначальной оценки связи между признаками.
Ранговый коэффициент корреляции вычисляется по формуле:
n -- число пар x,y (объём выборки). rxi -- ранг по признаку X ryi -- ранг по признаку Y. То есть ранги отдельно расставляются для XиY.
Так как RS эксп вычислен по выборке, то он также нуждается в проверке на достоверность. Для этого RS эксп сравнивают с RS критич , найденным в таблице ранговой корреляции ,для заданного уровня значимости α и числа степеней свободы n-2.
Н0: RS эксп не достоверен. Если |RS эксп| < RS критич то RS ,полученный по выборке не достоверен, корреляции (зависимости) между XиY нет. Если |RS эксп| ˃ RS критич то RS ,полученный по выборке достоверен, корреляция (зависимость) между XиY есть.
Пример: По критерию ранговой корреляции выяснить, есть ли корреляция между признаками XиY для уровня значимости α=0,05.
n=10 α=0,05 Н0: RS эксп не достоверен, корреляции нет.
По таблице ранговой корреляции для α=0,05 и числа степеней свободы 10-2=8 находим: RS критич=0,64. Так как Вывод: Ранговый коэффициент корреляции достоверен, корреляция между признаками XиY есть.
Вычислим параметрический коэффициент корреляции:
Проверка на достоверность: Н0: ρ=0,следовательно R[X,Y] не достоверен (то есть коэффициент корреляции генеральной совокупности ρ=0, следовательно зависимости между XиY нет).
В таблице критерия Стьюдента по заданному уровню значимости α=0,05 и числу степеней свободы: n-2=10-2=8 находим Так как симость (корреляция) между XиY есть. Построение линий регрессии:
Уравнение регрессии:

Контрольные вопросы.
Что такое корреляция? 2. Дисперсия суммы случайных величин. Корреляционный момент. Теорема сложения дисперсий. Параметрический коэффициент корреляции . Проверка параметрического коэффициента корреляции на достоверность. Построение линий регрессии. Ранговый коэффициент корреляции. Проверка рангового коэффициента корреляции на достоверность. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
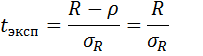
 где σR -- ошибка выборочного коэффициента корреляции R[X,Y]
где σR -- ошибка выборочного коэффициента корреляции R[X,Y] где n-2 число степеней свободы.
где n-2 число степеней свободы.
 .
. Н0 принимаем. Вывод: R недостоверен, за висимости между XиY нет.
Н0 принимаем. Вывод: R недостоверен, за висимости между XиY нет. Н0 отвергаем. Вывод: R достоверен, зависимость (корреляция) между XиY есть.
Н0 отвергаем. Вывод: R достоверен, зависимость (корреляция) между XиY есть.
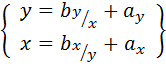




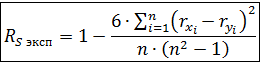

 Н0 отвергаем.
Н0 отвергаем.



