
|
|
Следствие. Если хотя бы для одного не крайнего коэффициента условие (2а) не выполняется, т.е.12
То имеется хотя бы одна пара комплексных корней. Методы уточнения корней Имеем: для уравнения (1) на интервале Рассмотрим четыре метода уточнения отделенных корней. Метод половинного деления Имеем: f(x)=0, а) f(x) – непрерывнана отрезке [ab], б) f(a)· f(b)< 0. Метод половинного деления состоит в построении путем деления пополам последовательности вложенных отрезков [ak,bk]
Рис. 2. К методу половинного деления
В соответствии с Рис.2 имеем: 1)
2)
………………………………………………………………………….
k)
Очевидно: Таким образом, метод половинного деления сходится к Достоинства: 1) прост в алгоритмизации и программировании; 2) на функцию f(x) не накладываются ограничения, кроме ее непрерывности. Недостаток: метод медленно сходится! На практике итерационный процесс останавливается при выполнении неравенства:
Метод Ньютона (метод касательных) В данном методе функция f(x) должна удовлетворять на отрезке 1) функция должна быть дважды дифференцируема; 2) 3)
Итерационный алгоритм в методе Ньютона имеет вид
x0=b или x0=a, где: xk – значение корня на k-ой итерации; hk=? – корректирующая поправка xk на k-ой итерации.
Требуется определить hk. Представим график функции f(x), удовлетворяющий условиям (*), на отрезке [a,b] на Рис.3 Пояснение метода Ньютона на Рис.3.
Рис.3. Метод Ньютона
Из
Аналогично из прямоугольного треугольника
В общем случае для (k+1)-ой итерации можно записать
Сходимость итерационного алгоритма (2*) или (3а) очевидна. Остановка итерационного алгоритма производится при выполнении условия
Достоинство – сходимость метода на порядок больше по сравнению с методом половинного деления. Недостатки: – более жесткие требования к f(x) (смотри (*)); – в каждой итерации необходимо вычислять
Метод секущих (хорд) Требования к f(x) такие же, как в методе Ньютона. Итерационный алгоритм метода секущих получается из итерационного алгоритма методом Ньютона (3а) заменой производной а) или б) При замене производной по формулеа) получим алгоритм метода секущих с неподвижным правым концом
Покажем графически алгоритм метода секущих с неподвижным правым концом, т.е. для условия а) Рис. 4. Метод секущих
Итерации сходятся к
Метод простых итераций Метод простых итераций уточнения корней уравнения (1) состоит в замене этого уравнения эквивалентным ему уравнением
и построении последовательности
Если не удается выразить х из уравнения (1), то эквивалентное уравнение и эквивалентную функцию x=x+f(x), Последовательность (6) называется методом простых итераций. Два вопроса: 1) сходится ли последовательность (6)? 2) если сходится, то является ли предел сходимости корнем Ответ на вопросы дает теорема о достаточном условии сходимости метода простой итерации к точному решению нелинейного уравнения, формирующаяся следующим образом: если функция Точность последовательности (6) определяется неравенством
или Остановка итерационного процесса (6) производится при выполнении где Действительно, на основании (7) максимальная величина ошибки на k-ой итерации равна
Учитывая требование
Геометрическая интерпретация сходимости метода простых итераций: Рис.5. Метод простой итерации
Метод простой итерации имеет линейную сходимость или первый порядок сходимости, т.е.
Пример: Уточнить отделённый корень на интервале (0.5, 1.0) с точностью
продолжить итерации до выполнения условия остановки.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, (a,b) отделен корень
(a,b) отделен корень  . Требуется уточнить отделенный корень с ошибкой, определяемой заданной величиной
. Требуется уточнить отделенный корень с ошибкой, определяемой заданной величиной  .
. (a,b), где
(a,b), где  [ak-1bk-1]
[ak-1bk-1]  [a0,b0 ]
[a0,b0 ]  [a,b], на концах которых удовлетворяются условия f(ak)·f(bk)<0, k=1,2,…, а вложенные отрезки определяются делением предыдущего отрезка пополам.
[a,b], на концах которых удовлетворяются условия f(ak)·f(bk)<0, k=1,2,…, а вложенные отрезки определяются делением предыдущего отрезка пополам. , вычисляется
, вычисляется  , если
, если 
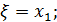
 2, иначе процесс деления продолжается:
2, иначе процесс деления продолжается: , вычисляется
, вычисляется  , если
, если 

 2
2  22, иначе процесс деления продолжается:
22, иначе процесс деления продолжается: , вычисляется
, вычисляется  , если
, если 

 2
2 
 - сходимость первого порядка
- сходимость первого порядка 
 а результатом является
а результатом является  .
. (x) ≠ 0; (*)
(x) ≠ 0; (*) , на отрезке [a,b].
, на отрезке [a,b]. , k=0,1,2,… (3)
, k=0,1,2,… (3) (прямоугольного) имеем
(прямоугольного) имеем  /
/  откуда
откуда  , тогда на основании (2а) имеем
, тогда на основании (2а) имеем
 получаем
получаем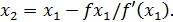
 (3а)
(3а)
 , а результатом является
, а результатом является 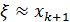 .
. и
и 
 ее приближенным значением
ее приближенным значением , если
, если  ,
, 
 , если
, если  ,
, 
 (4)
(4)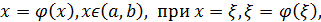 и
и  (5)
(5) (6)
(6) можно построить, например, так
можно построить, например, так и если существует число q такое, что на отрезке
и если существует число q такое, что на отрезке  выполняется неравенство
выполняется неравенство  , то последовательность (6) сходится к единственному корню уравнения (1) на интервале (a,b)при любом начальном приближении
, то последовательность (6) сходится к единственному корню уравнения (1) на интервале (a,b)при любом начальном приближении  .
. , (7)
, (7) . (7а)
. (7а)

 (8)
(8) - заданная точность вычисления корня
- заданная точность вычисления корня  (9)
(9) <
<  , что идентично с (8).
, что идентично с (8).




 иначе
иначе