
|
|
Граничные и начальные условияЛекция 4. Дифференциальные уравнения Эйлера Движения невязкой жидкости
Уравнения движения невязкой жидкости
Напряженное состояние жидкости, находящейся в покое, устанавливается уравнениями Эйлера. В процессе движения силы, действующие на жидкость, определяются не только напряжениями, но и скоростями. Использование уравнений статики для описания движения – принцип кинетостатики или принцип Д’Аламбера – состоит во введении сил инерции
Относя силы инерции к массе частицы жидкости, можно записать
Проекции удельной силы инерции выражаются через компоненты скорости
В соответствии с принципом Д’Аламбера уравнения движения принимают вид
Это уравнения идеальной (невязкой), несжимаемой жидкости, поскольку в них учитываются процессы внутреннего трения и связанные с ними касательные напряжения. В соответствии с примечанием к формулам (2.25) и (2.25а) в системе уравнений (4.4) приняты обозначения удельных массовых сил
Эквивалентные формы Уравнений невязкой несжимаемой жидкости
В зависимости от представления компонент ускорений можно записать следующие эквивалентные формы уравнений невязкой несжимаемой жидкости: а) в декартовой системе координат
б) в форме Громеки-Ламба при выполнении условий несжимаемости
Уравнение непрерывности
Замыкание системы уравнений движения невязкой жидкости производится с помощью уравнения неразрывности, выражающего закон сохранения массы.
Рис. 4.1. Движение жидкости сквозь элементарный объем Определим изменение расхода несжимаемой жидкости ( Если жидкость протекает через грани параллельные плоскости
Из условия баланса масс жидкости, входящей в элементарный объем и выходящей из него за время
(4.8) Для других пар граней запишем
Суммарное изменение массы равно
Поскольку в замкнутом объеме
Это дифференциальная форма уравнения неразрывности. Если движение жидкости потенциально, то проекции скорости на оси координат могут быть определены в виде
С учетом выражений для производных от компонент скорости по соответствующим координатам
получим уравнение Лапласа для безвихревого движения жидкости
где
Уравнение движения вязкой жидкости Навье-Стокса
Касательные напряжения вызываются трением. При отнесении сил трения к массе несжимаемой жидкости (
где Уравнение Рейнольдса
В случае пульсационного изменения скоростей в каждой точке потока действительная мгновенная скорость в соответствии с (3.3) равна
(4.15) Уравнение неразрывности для компонент осредненных скоростей имеет вид
Однако, система из трех уравнений Рейнольдса и уравнения неразрывности не являются замкнутыми. Недостающие уравнения полуэмпирическим путем определяют турбулентные напряжения
Граничные и начальные условия
Набор постоянных и функций, входящих в дифференциальные уравнения движения жидкости определяется дополнительными условиями, которые часто называются краевыми. Краевые условия включают граничные и начальные условия. Граничные условия формируются на границе области потока жидкости: 1) если граница является свободной поверхностью, то давление на ней постоянно 2) если поток ограничен твердой стенкой, то образуется условие непротекания и нормальная к стенке компонента скорости 3) вязкая жидкость «прилипает» к твердой стенке и 4) в живом сечении, ограничивающем поток, задается распределение скоростей. Начальные условия требуют знания о параметрах потока в момент времени

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (4.1)
. (4.1)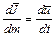 . (4.2)
. (4.2) ;
;  ;
;  . (4.3)
. (4.3)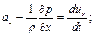
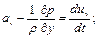 (4.4)
(4.4)
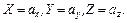


 (4.5)
(4.5)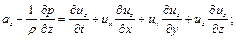
 и существования потенциала массовых сил
и существования потенциала массовых сил ;
; (4.6)
(4.6)

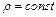 )при ее движении через элементарный объем с ребрами длиной
)при ее движении через элементарный объем с ребрами длиной 
 и
и  (рис.4.1). Масса жидкости
(рис.4.1). Масса жидкости 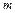 в выделенном объеме сохраняется, поэтому
в выделенном объеме сохраняется, поэтому 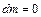 .
.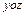 , то она входит в левую грань со скоростью
, то она входит в левую грань со скоростью 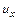 и выходит через противоположную грань со скоростью
и выходит через противоположную грань со скоростью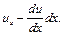 (4.7)
(4.7) , следует уравнение изменения потока массы
, следует уравнение изменения потока массы
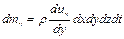 и
и  (4.9)
(4.9) (4.10)
(4.10) , то, после сокращения на
, то, после сокращения на 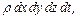 получим
получим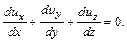 (4.11)
(4.11)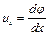 ,
, 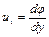 ,
, 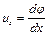 . (4.12)
. (4.12)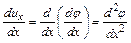 ;
;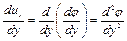 ;
;
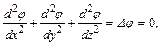 (4.13)
(4.13) - оператор Лапласа.
- оператор Лапласа. ) можно записать
) можно записать
 (4.14)
(4.14)
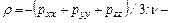 кинематическая вязкость.
кинематическая вязкость. с проекциями на оси координат
с проекциями на оси координат 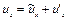 ,
, 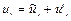 ,
,  . Из уравнений Навье-Стокса в результате замены действительных составляющих вектора скорости
. Из уравнений Навье-Стокса в результате замены действительных составляющих вектора скорости  на компоненты осредненных
на компоненты осредненных  и пульсационных
и пульсационных 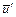 скоростей выводятся уравнения Рейнольдса
скоростей выводятся уравнения Рейнольдса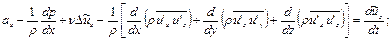
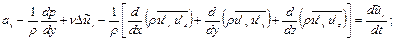

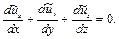 (4.16)
(4.16)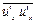 ,
, 
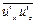 ,
, 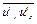 ,
, 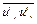 ,
,  ,
, 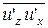 ,
, 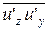 ,
,  .
.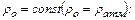
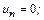
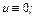
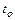 (обычно
(обычно 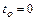 ). Например, при движении из состояния покоя
). Например, при движении из состояния покоя  а давление распределяется по гидростатическому закону
а давление распределяется по гидростатическому закону (4.17)
(4.17)