Решение системы (4) методом прогонки
Численное решение уравнения Шредингера
Уравнение Шредингера
 . (1) . (1)
В атомной системе единиц 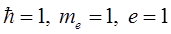
Масса протона 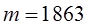 (далее полагаем (далее полагаем 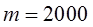 ) )
Исходное уравнение для волновой функции 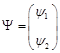 двухуровневой системы имеет вид, двухуровневой системы имеет вид,
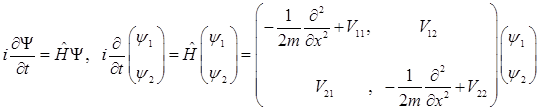 , (2) , (2)
Иными словами, мы имеем систему двух уравнений
 (3) (3)
(Левую и правую часть уравнения (2) умножили на 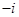 ) )
Если 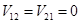 , то имеем два независимых уравнения. В этом случае переходы между уровнями не происходят. , то имеем два независимых уравнения. В этом случае переходы между уровнями не происходят.
Напишем неявную разностную схему для этой системы. Известные в момент времени  значения функций в узлах расчетной области будем обозначать синим цветом, а значения в момент времени значения функций в узлах расчетной области будем обозначать синим цветом, а значения в момент времени 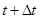 (которые нам необходимо определить) – красным. Для внутренних узлов расчетной области имеем систему линейных алгебраических уравнений: (которые нам необходимо определить) – красным. Для внутренних узлов расчетной области имеем систему линейных алгебраических уравнений:
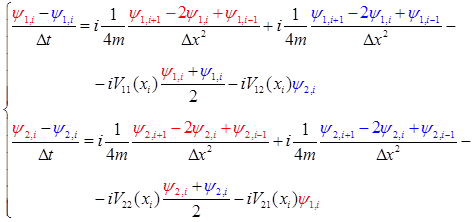 (4) (4)
Обратим внимание на важную деталь. Казалось бы, что во втором уравнении последнее слагаемое в правой части ( 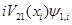 ) можно представить так, как это сделано в первом уравнении; т.е. ) можно представить так, как это сделано в первом уравнении; т.е. 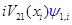 . Т.е. модифицировать разностную схему (4) к виду . Т.е. модифицировать разностную схему (4) к виду
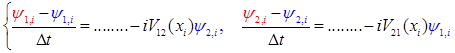 . (4b) . (4b)
Однако в таком варианте составленная разностная схема стала бы неустойчивой.
Для доказательства этого утверждения рассмотрим простейшую систему уравнений
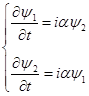 , где , где 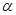 - некоторая константа. (5) - некоторая константа. (5)
Напишем явную разностую схему для этой системы
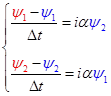 . (6) . (6)
Отсюда
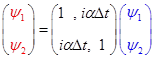 или или 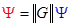 , (7) , (7)
Матрица  называется матрицей перехода. В общем случае ее размерность равна числу дифференциальных уравнений в системе. называется матрицей перехода. В общем случае ее размерность равна числу дифференциальных уравнений в системе.
Произведение матриц (7) выполняется для каждого шага по времени, т.е. многократно. Ошибки в значениях волновых функций 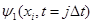 и и 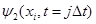 ( ( 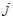 - номер шага по времени) приводят к ошибкам в значениях - номер шага по времени) приводят к ошибкам в значениях 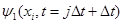 и и 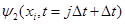 . Если ошибки лавинообразно нарастают от шага к шагу во времени, то используемая разностная схема неустойчива и может давать результат с удовлетворительной точностью только для ограниченного числа шагов, . Если ошибки лавинообразно нарастают от шага к шагу во времени, то используемая разностная схема неустойчива и может давать результат с удовлетворительной точностью только для ограниченного числа шагов, 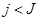 , причем определение предельного значения, , причем определение предельного значения, 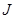 , может быть довольно сложной задачей. Следует строить численно устойчивые разностные схемы, которые не допускают лавинообразного накопления ошибок. , может быть довольно сложной задачей. Следует строить численно устойчивые разностные схемы, которые не допускают лавинообразного накопления ошибок.
Известно, что разностная схема устойчива только в том случае, если модуль собственных значений матрицы перехода  от известных в момент времени от известных в момент времени  величин, величин,  , к их значениям в момент , к их значениям в момент 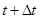 , , 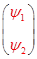 , не превышают единицы. , не превышают единицы.
Найдем эти собственные значения,  , из уравнения , из уравнения 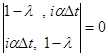 : : 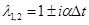 . .
Поскольку  , то ошибки аппроксимации и округления в процессе счета, , то ошибки аппроксимации и округления в процессе счета, 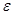 , будут нарастать во времени: , будут нарастать во времени: 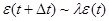 . Схема (6) неустойчива. . Схема (6) неустойчива.
Идеальной была бы неявная разностная схема второго порядка точности по 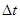
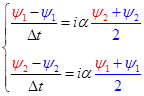 , (8) , (8)
в этом случае оба собственные значения матрицы перехода по модулю меньше единицы. Но аналогичная аппроксимация слагаемых  , , 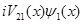 в системе (3) усложняет нахождение решения разностной схемы (4). в системе (3) усложняет нахождение решения разностной схемы (4).
Избежать этих сложностей можно приемом, который мы покажем на примере уравнения (5), записав разностную схему
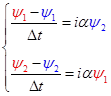 (9) (9)
Здесь явным образом находим 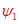 из первого уравнения и затем, так же явным образом, из первого уравнения и затем, так же явным образом, 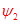 из второго. Неявной схему (8) называть нет оснований, но она устойчива! из второго. Неявной схему (8) называть нет оснований, но она устойчива!
Матрица перехода для схемы (9) 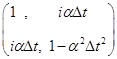 имеет собственные значения имеет собственные значения
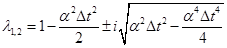 , и , и 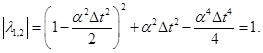
Таким образом, схема (9) хотя и не идеальна, но не допускает лавинообразного роста ошибок и является устойчивой. Представленный метод аппроксимации уравнений (5) разностной схемой (9) использован в построении разностной схемы (4).
Решение системы (4) методом прогонки
Для всех внутренних узлов расчетного интервала (с общим числом узлов  ) множество уравнений (4) представляет собой систему линейных ) множество уравнений (4) представляет собой систему линейных 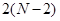 алгебраических уравнений относительно значений алгебраических уравнений относительно значений 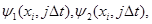 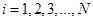 , , 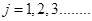 - номер шага по времени (начальным условиям - номер шага по времени (начальным условиям 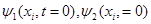 соответствует соответствует 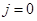 ). Разностная аппроксимация граничных условий для искомых функций (на левой и правой границах расчетного интервала) дает еще четыре алгебраических уравнения. Таким образом, число уравнений равно числу неизвестных, что делает возможным существование единственного решения для системы (4). ). Разностная аппроксимация граничных условий для искомых функций (на левой и правой границах расчетного интервала) дает еще четыре алгебраических уравнения. Таким образом, число уравнений равно числу неизвестных, что делает возможным существование единственного решения для системы (4).
Всю систему уравнений будем решать в два этапа. Сначала найдем значения функции 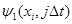 , а затем , а затем  . .
Каждое из разностных уравнений для 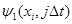 в (4) можно представить в виде: в (4) можно представить в виде:
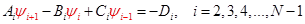 , (9) , (9)
где коэффициенты  для волной функции для волной функции 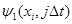 равны равны
 (10) (10)
(Коэффициенты 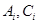 в нашем частном случае системы линейных параболических уравнений не зависят от номера внутренней точки.) в нашем частном случае системы линейных параболических уравнений не зависят от номера внутренней точки.)
Дополним систему (9) граничными условиями. Пусть, например, на правой границе 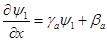 , а на правой , а на правой 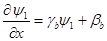 . Соотвествующая разностная аппроксимация этих условий: . Соотвествующая разностная аппроксимация этих условий:
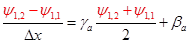 и и  . (11) . (11)
Отсюда
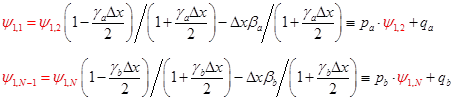 . (12) . (12)
Здесь
 . (13) . (13)
Систему уравнений (9), (12) можно представить в матричном виде :
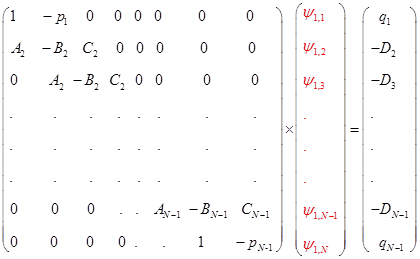 , (14) , (14)
или 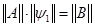 . .
Поскольку в матрице 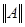 от нуля отличны только элементы, стоящие на трех центральных диагоналях, то решение (14) может быть найдено быстро и просто т.н. методом прогонки. от нуля отличны только элементы, стоящие на трех центральных диагоналях, то решение (14) может быть найдено быстро и просто т.н. методом прогонки.
Решение будем искать в виде
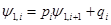 . (15) . (15)
Равенства (12),(13) дают нам 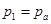 и и 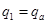 . Для вычисления остальных коэффициентов . Для вычисления остальных коэффициентов 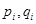 ( ( 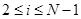 ) получим рекурентное соотношение (процедуру определения ) получим рекурентное соотношение (процедуру определения 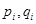 по уже найденным по уже найденным 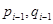 ). После подстановки в (9) (в соответствии с (15)) величины ). После подстановки в (9) (в соответствии с (15)) величины 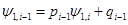 , получаем , получаем
.
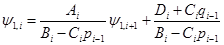 . (16) . (16)
Искомые рекурентные соотношения следуют из сопоставления (15) и (16):
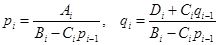 . (17) . (17)
Таким образом, процедура вычисления волновой функции 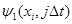 на на 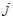 -ом шаге по времени (при уже известном дискретном множестве значений -ом шаге по времени (при уже известном дискретном множестве значений 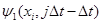 ) такова: ) такова:
- Вычисляем
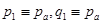 на основе заданного граничного условия на левой границе расчетной области (см. (12),(13)). на основе заданного граничного условия на левой границе расчетной области (см. (12),(13)).
- Строим цикл,
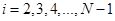 , в котором определяем значения коэффициентов , в котором определяем значения коэффициентов 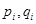 для внутренних узлов разностной сетки по рекурентным соотношениям (17). для внутренних узлов разностной сетки по рекурентным соотношениям (17).
- Находим крайне правое значение волновой функции
 . Для этого используем два представления . Для этого используем два представления 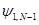 . С одной стороны, . С одной стороны, 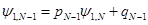 , а с другой – правое граничное условие дает , а с другой – правое граничное условие дает 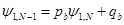 (см. (12),(13)). Отсюда (см. (12),(13)). Отсюда
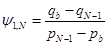 . (18) . (18)
- Строим обратный цикл,
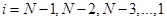 , в котором определяем остальные значения волновой функции , в котором определяем остальные значения волновой функции 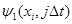 : : 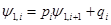 в соответствии с (15). в соответствии с (15).
- Аналогичную последовательность процедур выполняем для
 , завершая расчет одного шага по времени. , завершая расчет одного шага по времени.
- Все перечисленные выше операции повторяем многократно. Для анализа происходящего процесса периодически записываем в файлы волновые функции
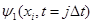 и и 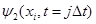 , а также физические величины (вероятности, импульсы, энергии), вычисляемые на основе этих волновых функций. Критерий окончания счета (полное число шагов по времени) устанавливаем из физических соображений с учетом особенностей поставленной задачи. , а также физические величины (вероятности, импульсы, энергии), вычисляемые на основе этих волновых функций. Критерий окончания счета (полное число шагов по времени) устанавливаем из физических соображений с учетом особенностей поставленной задачи.
Простые практические советы, снижающие реальное время расчетов. Следует заготовить различные константы во избежание их бесполезного многократно повторяющегося вычисления. Например, 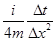 , , 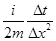 , , 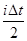 , , 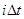 . Если нет проблем, связанных с дефицитом оперативной памяти, то в нашем случае можно заготовить даже массивы . Если нет проблем, связанных с дефицитом оперативной памяти, то в нашем случае можно заготовить даже массивы 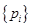 , которые не изменяются во времени. А так же массивы , которые не изменяются во времени. А так же массивы  , , 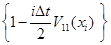 , , 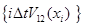 ( ( 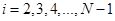 ; последние два массива нужны для быстрого вычисления ; последние два массива нужны для быстрого вычисления 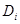 .) .)
Выбор начального состояния, шагов по координате,  , и по времени, , и по времени, 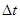 . .
Начальную волновую функцию частицы, 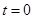 , задаем в виде волнового пакета , задаем в виде волнового пакета
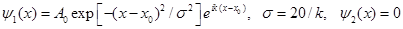 . (19) . (19)
Множитель 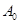 обеспечивает выполнение условия нормировки: обеспечивает выполнение условия нормировки: 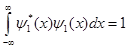 при при 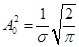 . .  - координата центра пакета, - координата центра пакета, 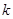 - волновой вектор, численно равный импульсу частицы в атомной системе единиц измерения ( - волновой вектор, численно равный импульсу частицы в атомной системе единиц измерения ( 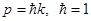 ). ).
Матричные элементы потенциала равны:
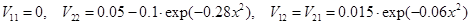 . (20) . (20)
Действительная,  , и мнимая части, , и мнимая части, 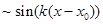 , функции (19) периодически изменяются в пространстве с длиной волны , функции (19) периодически изменяются в пространстве с длиной волны 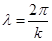 . Для корректного отображения волновой функции величина . Для корректного отображения волновой функции величина  должна быть в 100 и больше раз меньше, чем должна быть в 100 и больше раз меньше, чем  : :
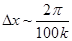 . (21) . (21)
Движение волнового пакета со скоростью 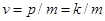 приводит к осцилляциям во времени действительной и мнимой частей волновой функции в фиксированной точке пространства с периодом приводит к осцилляциям во времени действительной и мнимой частей волновой функции в фиксированной точке пространства с периодом 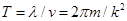 . Поэтому шаг по времени . Поэтому шаг по времени 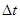 должен быть выбран порядка: должен быть выбран порядка:
 , (22) , (22)
поскольку 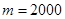 . .
При написании программы желательно ввести параметры  и и 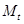 , которые управляют настройкой величин , которые управляют настройкой величин  : :
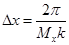 , , 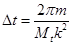 (23) (23)
для проверки корректности выбора шагов по времени и координате (выбор этих величин сделан правильно, если увеличение  , , 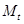 в в 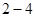 раза не изменяет результатов счета). раза не изменяет результатов счета).
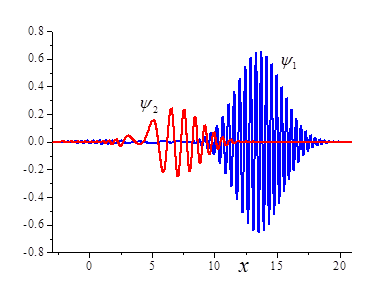
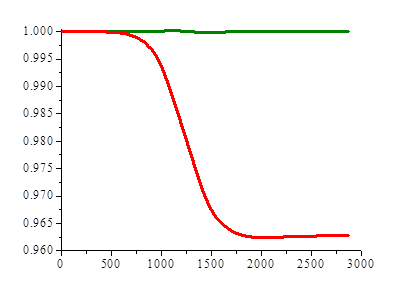
Начальное положение пакета,  , выбираем так, чтобы он был вне зоны взаимодействия ( , выбираем так, чтобы он был вне зоны взаимодействия (  ). На рис. 2 представлены зависимости плотности вероятности ). На рис. 2 представлены зависимости плотности вероятности 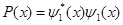 (при (при  ) и недиагонального элемента ) и недиагонального элемента 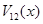 (каждая величина приведена в своих условных единицах, т.к. (каждая величина приведена в своих условных единицах, т.к. 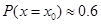 , а , а 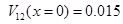 ). ).
Рис. 1.  построена для построена для  . .
С ростом волнового вектора ширина пакета уменьшается (см. (19)).
Отметим, что в начальный момент времени система находится на нижнем энергетическом уровне. Это легко заметить, записав уравнение (2) вне зоны потенциала:  , ,
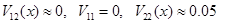 . .
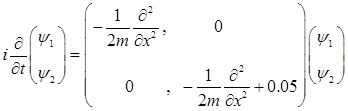 . (24) . (24)
Волновой функции  соотвествует потенциальная энергия 0, а волновой функции соотвествует потенциальная энергия 0, а волновой функции 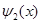 - потенциальная энергия 0.05. - потенциальная энергия 0.05.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 . (1)
. (1)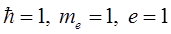
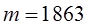 (далее полагаем
(далее полагаем 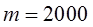 )
)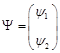 двухуровневой системы имеет вид,
двухуровневой системы имеет вид, , (2)
, (2) (3)
(3)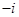 )
)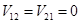 , то имеем два независимых уравнения. В этом случае переходы между уровнями не происходят.
, то имеем два независимых уравнения. В этом случае переходы между уровнями не происходят. значения функций в узлах расчетной области будем обозначать синим цветом, а значения в момент времени
значения функций в узлах расчетной области будем обозначать синим цветом, а значения в момент времени 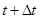 (которые нам необходимо определить) – красным. Для внутренних узлов расчетной области имеем систему линейных алгебраических уравнений:
(которые нам необходимо определить) – красным. Для внутренних узлов расчетной области имеем систему линейных алгебраических уравнений: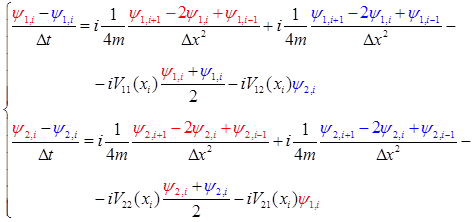 (4)
(4)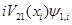 ) можно представить так, как это сделано в первом уравнении; т.е.
) можно представить так, как это сделано в первом уравнении; т.е. 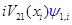 . Т.е. модифицировать разностную схему (4) к виду
. Т.е. модифицировать разностную схему (4) к виду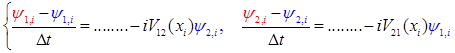 . (4b)
. (4b)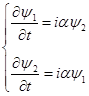 , где
, где  - некоторая константа. (5)
- некоторая константа. (5)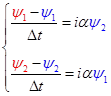 . (6)
. (6)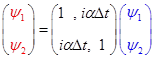 или
или  , (7)
, (7) называется матрицей перехода. В общем случае ее размерность равна числу дифференциальных уравнений в системе.
называется матрицей перехода. В общем случае ее размерность равна числу дифференциальных уравнений в системе. и
и 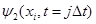 (
( 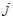 - номер шага по времени) приводят к ошибкам в значениях
- номер шага по времени) приводят к ошибкам в значениях 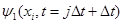 и
и 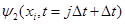 . Если ошибки лавинообразно нарастают от шага к шагу во времени, то используемая разностная схема неустойчива и может давать результат с удовлетворительной точностью только для ограниченного числа шагов,
. Если ошибки лавинообразно нарастают от шага к шагу во времени, то используемая разностная схема неустойчива и может давать результат с удовлетворительной точностью только для ограниченного числа шагов, 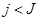 , причем определение предельного значения,
, причем определение предельного значения, 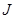 , может быть довольно сложной задачей. Следует строить численно устойчивые разностные схемы, которые не допускают лавинообразного накопления ошибок.
, может быть довольно сложной задачей. Следует строить численно устойчивые разностные схемы, которые не допускают лавинообразного накопления ошибок. , к их значениям в момент
, к их значениям в момент 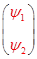 , не превышают единицы.
, не превышают единицы. , из уравнения
, из уравнения 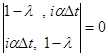 :
: 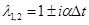 .
. , то ошибки аппроксимации и округления в процессе счета,
, то ошибки аппроксимации и округления в процессе счета, 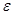 , будут нарастать во времени:
, будут нарастать во времени: 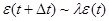 . Схема (6) неустойчива.
. Схема (6) неустойчива.
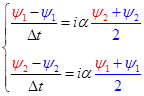 , (8)
, (8) ,
, 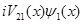 в системе (3) усложняет нахождение решения разностной схемы (4).
в системе (3) усложняет нахождение решения разностной схемы (4).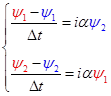 (9)
(9)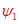 из первого уравнения и затем, так же явным образом,
из первого уравнения и затем, так же явным образом, 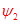 из второго. Неявной схему (8) называть нет оснований, но она устойчива!
из второго. Неявной схему (8) называть нет оснований, но она устойчива!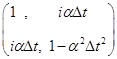 имеет собственные значения
имеет собственные значения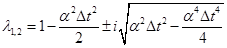 , и
, и 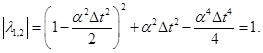
 ) множество уравнений (4) представляет собой систему линейных
) множество уравнений (4) представляет собой систему линейных 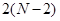 алгебраических уравнений относительно значений
алгебраических уравнений относительно значений 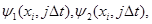
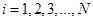 ,
, 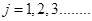 - номер шага по времени (начальным условиям
- номер шага по времени (начальным условиям 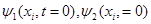 соответствует
соответствует 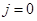 ). Разностная аппроксимация граничных условий для искомых функций (на левой и правой границах расчетного интервала) дает еще четыре алгебраических уравнения. Таким образом, число уравнений равно числу неизвестных, что делает возможным существование единственного решения для системы (4).
). Разностная аппроксимация граничных условий для искомых функций (на левой и правой границах расчетного интервала) дает еще четыре алгебраических уравнения. Таким образом, число уравнений равно числу неизвестных, что делает возможным существование единственного решения для системы (4).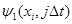 , а затем
, а затем  .
.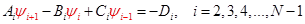 , (9)
, (9) для волной функции
для волной функции  (10)
(10)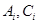 в нашем частном случае системы линейных параболических уравнений не зависят от номера внутренней точки.)
в нашем частном случае системы линейных параболических уравнений не зависят от номера внутренней точки.)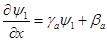 , а на правой
, а на правой 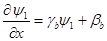 . Соотвествующая разностная аппроксимация этих условий:
. Соотвествующая разностная аппроксимация этих условий: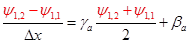 и
и  . (11)
. (11)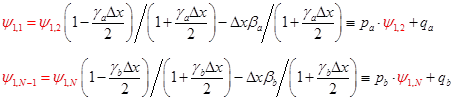 . (12)
. (12) . (13)
. (13)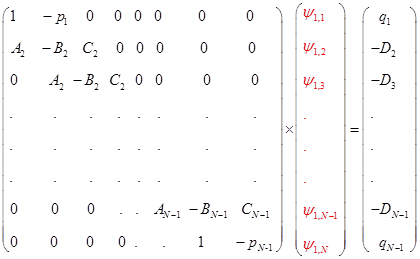 , (14)
, (14)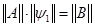 .
.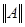 от нуля отличны только элементы, стоящие на трех центральных диагоналях, то решение (14) может быть найдено быстро и просто т.н. методом прогонки.
от нуля отличны только элементы, стоящие на трех центральных диагоналях, то решение (14) может быть найдено быстро и просто т.н. методом прогонки.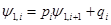 . (15)
. (15)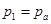 и
и 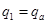 . Для вычисления остальных коэффициентов
. Для вычисления остальных коэффициентов 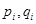 (
( 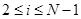 ) получим рекурентное соотношение (процедуру определения
) получим рекурентное соотношение (процедуру определения 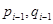 ). После подстановки в (9) (в соответствии с (15)) величины
). После подстановки в (9) (в соответствии с (15)) величины 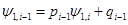 , получаем
, получаем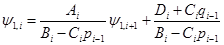 . (16)
. (16)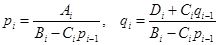 . (17)
. (17)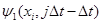 ) такова:
) такова: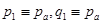 на основе заданного граничного условия на левой границе расчетной области (см. (12),(13)).
на основе заданного граничного условия на левой границе расчетной области (см. (12),(13)).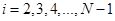 , в котором определяем значения коэффициентов
, в котором определяем значения коэффициентов  . Для этого используем два представления
. Для этого используем два представления 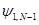 . С одной стороны,
. С одной стороны, 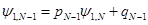 , а с другой – правое граничное условие дает
, а с другой – правое граничное условие дает 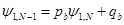 (см. (12),(13)). Отсюда
(см. (12),(13)). Отсюда 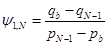 . (18)
. (18)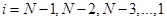 , в котором определяем остальные значения волновой функции
, в котором определяем остальные значения волновой функции 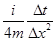 ,
, 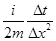 ,
, 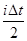 ,
, 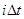 . Если нет проблем, связанных с дефицитом оперативной памяти, то в нашем случае можно заготовить даже массивы
. Если нет проблем, связанных с дефицитом оперативной памяти, то в нашем случае можно заготовить даже массивы 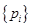 , которые не изменяются во времени. А так же массивы
, которые не изменяются во времени. А так же массивы  ,
, 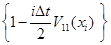 ,
, 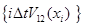 (
( 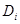 .)
.) , и по времени,
, и по времени, 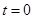 , задаем в виде волнового пакета
, задаем в виде волнового пакета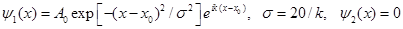 . (19)
. (19)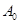 обеспечивает выполнение условия нормировки:
обеспечивает выполнение условия нормировки: 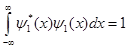 при
при 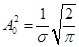 .
.  - координата центра пакета,
- координата центра пакета, 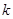 - волновой вектор, численно равный импульсу частицы в атомной системе единиц измерения (
- волновой вектор, численно равный импульсу частицы в атомной системе единиц измерения ( 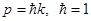 ).
).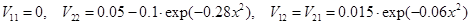 . (20)
. (20) , и мнимая части,
, и мнимая части, 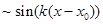 , функции (19) периодически изменяются в пространстве с длиной волны
, функции (19) периодически изменяются в пространстве с длиной волны 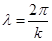 . Для корректного отображения волновой функции величина
. Для корректного отображения волновой функции величина 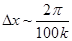 . (21)
. (21)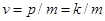 приводит к осцилляциям во времени действительной и мнимой частей волновой функции в фиксированной точке пространства с периодом
приводит к осцилляциям во времени действительной и мнимой частей волновой функции в фиксированной точке пространства с периодом 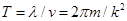 . Поэтому шаг по времени
. Поэтому шаг по времени  , (22)
, (22)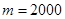 .
. и
и 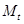 , которые управляют настройкой величин
, которые управляют настройкой величин  :
: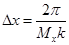 ,
, 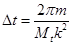 (23)
(23) раза не изменяет результатов счета).
раза не изменяет результатов счета). ). На рис. 2 представлены зависимости плотности вероятности
). На рис. 2 представлены зависимости плотности вероятности 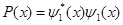 (при
(при  ) и недиагонального элемента
) и недиагонального элемента 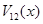 (каждая величина приведена в своих условных единицах, т.к.
(каждая величина приведена в своих условных единицах, т.к. 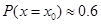 , а
, а 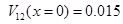 ).
). построена для
построена для  ,
,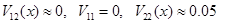 .
.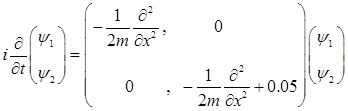 . (24)
. (24) соотвествует потенциальная энергия 0, а волновой функции
соотвествует потенциальная энергия 0, а волновой функции 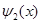 - потенциальная энергия 0.05.
- потенциальная энергия 0.05.

