
|
|
Метод половинного деленияЧисленные методы решения нелинейного уравнения С одним неизвестным Постановка задачи Дано уравнение F(x)=0. Это - общий вид нелинейного уравнения с одним неизвестным. Решить уравнение означает найти его корни, то есть такие значения аргумента x, которые при подстановке превращают уравнение в тождество. Далеко не все уравнения решаются аналитически. Например, квадратное уравнение типа ax2 + bx + c = 0 легко решается аналитически и имеет два корня: Приближенное нахождение изолированных корней уравнения состоит из двух этапов: 1. отделение корней, т. е. установление конечных или бесконечных интервалов на области определения функции, содержащих только один корень уравнения; 2. уточнение корней, т. е. доведение их до заданной точности. Уточнение приближенного значения корня до некоторой точности.
На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней. В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается аналитическими и графическими методами. Графически корни можно отделить 2-мя способами:
 
 
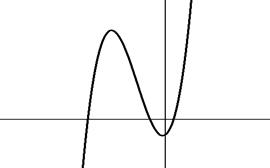
Рис. 3.1 Отделение корней на графике f(x).
Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).
Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.
На втором этапе используется один из методов уточнения (например, метод половинного деления, метод Ньютона, метод простой итерации). Рассмотрим более подробно эти методы.
Шаговый метод Дано уравнение F(x)=0. Задан интервал поиска [x0,x1]. Требуется найти интервал [a,b] длиной h, содержащий первый корень уравнения, начиная с левой границы интервала поиска. Алгоритм метода: Установить интервал [a,b] на начало интервала поиска (a=x0). Определить координату точки b (b=a+h), а также значения функции в точках a и b: F(a) и F(b). Проверить условие F(a)*F(b)<0. Если условие не выполнено - передвинуть интервал [a,b] на один шаг (a=b) и перейти к пункту 2. Если условие выполнено - закончить алгоритм. Решением являются координаты точек a и b. Отрезок [a,b] содержит корень уравнения, поскольку функция F(x) на его концах имеет разные знаки (рис .3.3).
Рис. 3.3 Иллюстрация шагового метода
Найдя первый корень, можно продолжить поиск корней по тому же алгоритму. В этом случае определяются отрезки, содержащие все корни уравнения на интервале поиска [x0,x1]. Если на всем интервале поиска ни разу не было выполнено условие F(a)*F(b)<0, то данный интервал вообще не содержит корней. Рассмотрим пример ручной реализации метода. Дано уравнение x2 – 4x + 3 = 0 и интервал поиска корня [0;2]. Требуется отделить первый корень уравнения шаговым методом с шагом h=0,3. Построим таблицу в соответствии с алгоритмом метода.
Ответ: корень расположен на интервале [0,9;1,2]. Достоинство метода: простота алгоритма. Недостаток: для достижения большой точности требуется уменьшать шаг, а это может существенно увеличить время расчета.
Метод половинного деления Метод основан на последовательном сужении интервала, содержащего единственный корень уравнения F(x)=0 до тех пор, пока не будет достигнута заданная точность e. Пусть задан отрезок [a,b], содержащий один корень уравнения. Этот отрезок может быть предварительно найден с помощью шагового метода. Рис. 3.4. иллюстрирует метод половинного деления, который состоит в постепенном сужении отрезка поиска корня до заданной величины e. На каждом шаге отрезок уменьшается вдвое.
Рис. 3.4. Иллюстрация метода половинного деления В начале каждой итерации находим середину нового отрезка [a , b] Затем следует определить, с какой стороны от середины отрезка x находится корень x*. Для этого достаточно сравнить знаки f (x) и f (b) или знаки f (x) и f (a). Если знаки f (x) и f (b) не совпадают, то это означает, что f (x) пересекает ось x на правом полуотрезке [x, b]. Следовательно, корня нет на левом полуотрезке [a, x], и этот полуотрезок можно отбросить, то есть можно перенести левую границу a в среднюю точку x (заменить значение приближения a на значение x). Если же знаки f (x) и f (b) совпадают, то f (x) пересекает ось x на левом полуотрезке [a, x] и, следовательно, корня нет на правом полуотрезке [x ,b], и этот полуотрезок можно отбросить, то есть можно перенести правую границу b в среднюю точку x (заменить значение приближения b на значение x). Итак, в результате выполнения итерации отрезок [a, b] как и прежде, содержит единственный корень, но его длина стала меньше в два раза. Вычисления следует прекратить, если на очередном шаге длина отрезка [a, b] станет меньше e. Тогда с точностью e любая точка этого отрезка будет являться корнем уравнения f(x), а середина этого отрезка - с точностью e/2. Рассмотрим пример ручной реализации метода. Дано уравнение x2 – 4x + 3 = 0. Известно, что единственный корень уравнения расположен на отрезке [0,9;1,2]. Требуется уточнить значение корня методом половинного деления с точностью e = 0,01. Построим таблицу в соответствии с алгоритмом метода.
Алгоритм остановлен, поскольку ï-0,00624ï<0,01. Ответ: уточненное значение корня x » 1,0031.
Достоинство метода: более быстрая сходимость к заданной точности, чем у шагового. Недостаток: если на отрезке [a,b] содержится более одного корня, то метод не работает. Кроме того, метод дихотомии нельзя использовать, если корень совпадает с точкой экстремума функции, т.к. в этом случае функция не изменяет свой знак в окрестности корня.
Рис. 3.5. Корень является экстремумом функции (функция не меняет знак)
3.5. Метод Ньютона Задан отрезок [a,b], содержащий корень уравнения F(x)=0. Уточнение значения корня производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [a,b], где значение функции и ее второй производной имеют одинаковые знаки (т.е. выполняется условие F(x0)*F¢¢(x0)>0). В точке F(x0) строится касательная к кривой y= F(x) и ищется ее пересечение с осью x. Точка пересечения принимается за новую итерацию. Итерационная формула имеет вид:
Итерационный процесс продолжается до тех пор, пока не будет выполнено условие ïF(x)<eï, где e - заданная точность.
Рис. 3.6. Иллюстрация метода Ньютона (1) В качестве начального приближения можно взять также середину отрезка [a,b]:
Рис. 3.7 Иллюстрация метода Ньютона(2)
Если на отрезке существования корня знаки
Рис. 3.13. Геометрическая иллюстрация выбора начального приближения: график f(x) вогнутый,
Если же выбрать x0=a, то итерационный процесс будет сходиться медленнее или даже расходиться (см. касательную для x0=a).
●
Рис. 3.14. Геометрическая иллюстрация выбора начального приближения: график f(x) выпуклый, f ’’(x)<0 , тогда x0 =a, т.к. f(a)<0.
Метод Ньютона в отличие от ранее рассмотренных методов используют свойства функции в виде значения производной, что значительно ускоряет итерационный процесс. При этом, чем больше значение модуля производной в окрестности корня (чем круче график функции), тем быстрее сходимость.
Рассмотрим пример ручной реализации метода. Дано уравнение x2 – 4x + 3 = 0. Известно, что корень уравнения расположен на отрезке [0,9;1,2]. Требуется уточнить значение корня методом Ньютона с точностью e = 0,001. Найдем первую и вторую производную функции F(x). F’(x)= 2x – 4; F”(x) = 2. F(0,9) = 0,21; F(1,2) = -0,36. Следовательно, в качестве начального приближения выбираем точку x0 = a = 0,9. Построим таблицу в соответствии с алгоритмом метода.
Ответ: уточненное значение корня x » 0,99999. Достоинство метода: очень быстрая сходимость к заданной точности. Недостатки: громоздкий алгоритм: на каждой итерации необходимо вычислять значение функции и ее первой производной, сильная зависимость сходимости от вида функции и выбора начального приближения. Метод простой итерации Метод основан на замене исходного уравнения F(x)=0 на эквивалентное x=j(x). Функция j(x) выбирается таким образом, чтобы на обоих концах отрезка [a,b] выполнялось условие сходимости êj¢(x) ê < 1. В этом случае в качестве начального приближения можно выбрать любой из концов отрезка. Итерационная формула имеет вид
Итерационный процесс продолжается до тех пор, пока не будет выполнено условие ïF(x)ï<e, где e - заданная точность. Рассмотрим геометрическую иллюстрацию метода простых итераций. Уравнение представим на графике в виде двух функций: y1 = x и y2= φ(x). Возможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рисунках
Рис. 3.8 Итерационный процесс для случая 0<
Рис. 3.9 Итерационный процесс для случая -1<
Рис. 3.11. Иллюстрация метода простой итерации
Из анализа графиков следует, что скорость сходимости растет при уменьшении значения
Метод достаточно прост, обобщается на системы уравнений, устойчив к погрешности округления (она не накапливается). При разработке алгоритма решения нелинейного уравнения методом простых итераций следует предусмотреть защиту итерационного процесса от зацикливания: использовать в качестве дополнительного условия завершения итерационного процесса превышение заданного максимального числа итераций.
Основной проблемой применения метода является обеспечение сходимости итерационного процесса: нужно найти такое эквивалентное преобразование чтобы обеспечивалось условие сходимости. Простейшие эквивалентные преобразования, например: f(x) = 0 => x+f(x) = x, т.е. φ(x) = x + f(x) или выразить явно x f(x) = 0 => x - φ(x) = 0 => x = φ(x) не гарантируют сходимость. Рекомендуется следующий способ получения формулы сходящегося итерационного процесса.
Если это не так, умножить обе части уравнения на и к обеим частям прибавить x:
Константу l вычислить по формуле:
Такое значение λ гарантирует сходящийся итерационный процесс по формуле xi = xi+1− λ f(x) где i=1,2,… - номер итерации, x0Î[a,b] – начальное приближение. Рассмотрим пример ручной реализации метода. Дано уравнение x2 – 4x + 3 = 0. Известно, что корень уравнения расположен на отрезке [0,9;1,2]. Требуется уточнить значение корня методом простой итерации с точностью e = 0,03. На первом этапе нам необходимо выбрать функцию j(x), удовлетворяющую условию сходимости. Запишем исходное уравнение в виде x = x2 – 3x + 3. Тогда j(x) = x2 – 3x + 3; j¢(x) = 2x – 3; j¢(0,9) = -1,2; j¢(1,2) = -0,6. Условие сходимости не выполнено, поскольку ê-1,2 ê > 1. Запишем исходное уравнение в виде Запишем исходное уравнение в виде Следовательно, итерационная формула имеет вид:
В качестве начального приближения можно выбрать любой из концов отрезка, например x0 = a = 0,9. Построим таблицу в соответствии с алгоритмом метода.
Ответ: уточненное значение корня x » 0,9885.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . В то же время уравнение типа axn + bx + c = 0 в общем случае не имеет аналитического решения. Еще сложнее обстоит дело с уравнениями типа
. В то же время уравнение типа axn + bx + c = 0 в общем случае не имеет аналитического решения. Еще сложнее обстоит дело с уравнениями типа 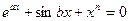 . В общем случае, если нелинейное уравнение не решается аналитическими методами, целесообразно применение численных методов с использованием ЭВМ.
. В общем случае, если нелинейное уравнение не решается аналитическими методами, целесообразно применение численных методов с использованием ЭВМ.

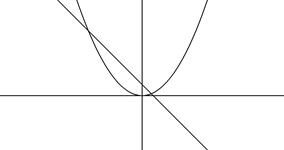









 и
и  не изменяются, то начальное приближение, обеспечивающее сходимость, нужно выбрать из условия
не изменяются, то начальное приближение, обеспечивающее сходимость, нужно выбрать из условия , x0Î[a;b].
, x0Î[a;b]. т.е. в точке начального приближения знаки функций и ее второй производной должны совпадать.
т.е. в точке начального приближения знаки функций и ее второй производной должны совпадать. , тогда x0=b, т.к. f(b)>0.
, тогда x0=b, т.к. f(b)>0.



 <1
<1  xÎ[a,b].
xÎ[a,b].

 Рис. 3.10. Итерационный процесс для случая
Рис. 3.10. Итерационный процесс для случая 
 Пусть
Пусть  .
.

 . Тогда
. Тогда 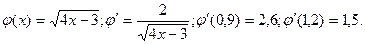 Условие сходимости не выполнено, поскольку ê2,6 ê > 1; ê1,5 ê > 1.
Условие сходимости не выполнено, поскольку ê2,6 ê > 1; ê1,5 ê > 1. Условие сходимости выполнено.
Условие сходимости выполнено.