
|
|
Дифференциальные уравнения, их порядок, общий и частные интегралы12 Введение
Целью настоящих методических указаний является помощь студентам – заочникам в выполнении контрольной работы №3. Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях. Номер варианта по каждому заданию студент выбирает по формуле где
Пример. Пусть шифр студента 1235, тогда: номер варианта первого задания: номер варианта второго задания: номер варианта третьего задания: номер варианта четвертого задания: Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом. Если итоговая число по формуле получится больше 20, то для определения варианта от полученного числа отнимают 20.
Пример. Пусть шифр студента 1298. Номер варианта второго задания: Основная цель инженера – исследователя, изучающего какой- либо физический или технический процесс, заключается в выявлении его закономерностей, в получении аналитического выражения функциональной зависимости между переменными параметрами этого процесса. Большинство подобных задач сводится к решению уравнений, содержащих производные или дифференциалы неизвестных функций.
Дифференциальные уравнения, их порядок, общий и частные интегралы Дифференциальным уравнениемназывается равенство, содержащее производные или дифференциалы неизвестной функции. Если неизвестная функция зависит только от одного аргумента, то дифференциальное уравнение называется обыкновенным, а если она зависит от нескольких аргументов и дифференциальное уравнение содержит ее частные производные по этим аргументам, то оно называется уравнением с частными производными. Будем рассматривать обыкновенные дифференциальные уравнения. Порядком дифференциального уравнения называется порядок высшей производной, содержащейся в этом уравнении. Функция, удовлетворяющая дифференциальному уравнению, т.е. обращающая его в тождество, называется интегралом (решением) данного уравнения. Интеграл дифференциального уравнения, называется общим, если он содержит столько независимых произвольных постоянных, каков порядокуравнения. А функции, получаемые из общего интеграла при различных числовых значениях произвольных постоянных, называются частными интегралами этого уравнения. Отыскание частного интеграла дифференциального уравнения, удовлетворяющего начальным условиям, называется задачей Коши.
1.1 Дифференциальные уравнения первого порядка Уравнение с разделенными переменными Общий вид: Его общий интеграл:
Уравнение с разделяющимися переменными Его общий вид: Разделяя переменные:
Однородное дифференциальное уравнение первого порядка Это уравнение вида: Уравнение первого порядка Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой у=ux (или x=uy), где u=u(x) ( u=u(y) )- новая функция.
Пример 1. Найти общий интеграл данного уравнения:
Решение: Это однородное уравнение, т.к. Далее вводим новую функцию Разделим переменные: Линейные уравнения первого порядка Это уравнения вида: Посредством замены функции Пример 2 Решить уравнение Решение: Убедившись, что данное уравнение линейное, полагаем
Так как одну из вспомогательных функций Тогда для отыскания Решая первое уравнение, найдем
Подставляя v во второе уравнение и решая его, найдем Зная
Уравнение Бернулли Его общий вид:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,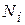 - номер варианта,
- номер варианта, -номер задания,
-номер задания,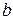 -предпоследняя цифра шифра студента,
-предпоследняя цифра шифра студента, -последняя цифра шифра.
-последняя цифра шифра.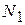 =
=  ;
; ;
; ;
; .
.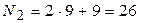 . Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу варианта №6.
. Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу варианта №6.
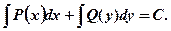
 или
или 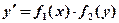 .
.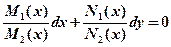 , получаем дифференциальное уравнение с разделенными переменными.
, получаем дифференциальное уравнение с разделенными переменными. если функция
если функция  удовлетворяет условию
удовлетворяет условию  , k=const
, k=const называется однородным, если
называется однородным, если  можно представить как функцию только одного отношения переменных
можно представить как функцию только одного отношения переменных  , т.е. уравнения вида
, т.е. уравнения вида  .
.
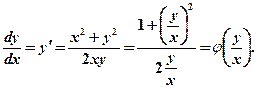
 , полагая
, полагая  при этом
при этом  и после подстановки данное уравнение преобразуется в уравнение с разделяющимися переменными
и после подстановки данное уравнение преобразуется в уравнение с разделяющимися переменными 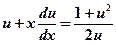 или
или 
 и, интегрируя, найдем
и, интегрируя, найдем  или
или  . Исключая вспомогательную функцию
. Исключая вспомогательную функцию 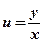 , окончательно получим
, окончательно получим 
 , где
, где  и
и  - известные функции от х.
- известные функции от х. произведением двух вспомогательных функций
произведением двух вспомогательных функций  линейное уравнение сводится к двум уравнениям с разделяющимися переменными относительно каждой из вспомогательных функций.
линейное уравнение сводится к двум уравнениям с разделяющимися переменными относительно каждой из вспомогательных функций.
 тогда
тогда 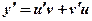 и данное уравнение преобразуется к виду:
и данное уравнение преобразуется к виду: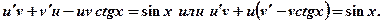
 или
или  (1)
(1)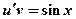 (2)
(2)
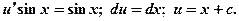

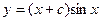 .
. . Данное уравнение отличается от линейного тем, что в правую часть входит множителем некоторая степень функции
. Данное уравнение отличается от линейного тем, что в правую часть входит множителем некоторая степень функции  сводится к двум уравнениям с разделяющимися переменными.
сводится к двум уравнениям с разделяющимися переменными.