
|
|
Изучение прецессии гироскопа. (Лабораторная работа 11)
Приборы и принадлежности: гироскоп FРМ-10 или ФМ-18 М.
Теория метода и описание прибора В этой работе определяется скорость прецессии гироскопа Ω и проверяются отношения:
Рассмотрим гироскоп, состоящий из диска, который может вращаться вокруг горизонтальной оси О1О2 (рис. 5.4) и противовеса К. Ось гироскопа О1О2 шарнирно закреплена в точке О1 вертикальной подставки. Противовес К можно перемещать вдоль оси. Если противовес К расположен таким образом, что точка О1 является центром тяжести, т.е.
получим
где
Гироскоп обладает постоянным моментом импульса Передвинем противовес К на небольшое расстояние вправо. Центр тяжести системы переместится в точку О' (рис. 5.5). Равновесие нарушится, ось гироскопа будет составлять с вертикалью угол j. В этом случае момент силы
где
Из уравнения (5.18) следует, что изменение момента импульса
Результирующий момент
Это означает, что ось гироскопа изменит свое положение в горизонтальной плоскости, повернувшись за время dt на угол da. За последующий промежуток времени снова произойдет изменение момента импульса на Величина
называется угловой скоростью прецессии. Вычислим ее значение. Из формул (5.20) и (5.21) следует, что
Из рис. 5.5 следует, что
Подставим выражение (5.24) в формулу (5.22):
или Из уравнения (5.25) следует, что с увеличением угловой скорости вращения гироскопа ω угловая скорость прецессии W уменьшается. Если скорость вращения диска постоянна w = const, то отношение Описание прибора
Прибор представлен на рис. 5.6. На основании (1), оснащенном ножками с регулируемой высотой, позволяющем произвести выравнивание прибора, закреплена колонка с кронштейном, на котором установлен фотоэлектрический датчик и внешняя втулка вращательного соединения (2). Электрический двигатель смонтирован на кронштейне (3). Рычаг (4), закрепленный на корпусе двигателя, имеет миллиметровую шкалу. На рычаге закреплен груз – противовес (5). С помощью указателя (6) можно определить по шкале (7) угол поворота гороскопа вокруг вертикальной оси. Диск (7) имеет на окружности отверстия через каждые 5°, которые с помощью фотоэлемента позволяют давать информацию об угле оборота гироскопа. На лицевой панели блока управления (8) находятся следующие манипуляционные элементы: СЕТЬ, СБРОС, СТОП, РЕГ. СКОРОСТЬ. Время запуска гироскопа 2 минуты. Порядок выполнения работы и обработка результатов Измерений 1. Перемещая груз (5), установить рычаг гироскопа перпендикулярно оси, чтобы ось гироскопа была горизонтальной. 2. Включить питание двигателя. 3. Отрегулировать обороты двигателя 6000 об/мин. 4. Переместить груз на 2 см от положения равновесия. 5. Нажать кнопку "Сброс". 6. После показания времени не менее 30 с нажать "Стоп". 7. Снять показания угла αi и времени ti прецессии. 8. Вычислить угловую скорость прецессии по формуле 9. Изменяя положение груза на 2 см, повторить измерения. При этом ось гироскопа каждый раз ориентировать в исходное состояние, одинаковое при всех измерениях. Таблица 5.2
10. Построить график зависимости W = f(r) и убедиться в его линейности. 11. Проверить соотношения Контрольные вопросы 1. Сформулируйте цели работы. 2. Как определяются направления векторов: углового перемещения, угловой скорости, углового ускорения? 3. Запишите выражения для момента импульса относительно точки и относительно неподвижной оси. 4. Сформулируйте 2-ой закон динамики для вращательного движения. 5. Запишите выражение момента сил относительно точки. 6. Сформулируйте закон сохранения момента импульса. 7. Что называется гироскопом? 8. Куда направлен вектор момента импульса гироскопа? 9. Каково направление вектора момента сил гироскопа? С каким вектором совпадает направление момента сил? 10. Запишите условие равновесия системы. 11. Какое движение называется прецессией? Чему равна угловая скорость прецессии? 12. Как изменится скорость прецессии с изменением угловой скорости вращения? 13. Сделайте выводы по работе.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


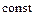
 Рис. 5.4
Рис. 5.4
 , где F1 и F2 – силы тяжести диска и противовеса, l1 и l2 плечи сил, то результирующий момент сил, действующих на систему, равен нулю (М=О). В противном случае система отклонилась бы от положения равновесия. Пусть диск уравновешенной системы вращается с угловой скоростью ω. В этом случае на основании II закона динамики для вращательного движения
, где F1 и F2 – силы тяжести диска и противовеса, l1 и l2 плечи сил, то результирующий момент сил, действующих на систему, равен нулю (М=О). В противном случае система отклонилась бы от положения равновесия. Пусть диск уравновешенной системы вращается с угловой скоростью ω. В этом случае на основании II закона динамики для вращательного движения (5.18)
(5.18) , (5.19)
, (5.19)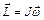 – момент импульса диска. Из уравнения (5.19) следует, что вектор момента импульса в этом случае не зависит от времени:
– момент импульса диска. Из уравнения (5.19) следует, что вектор момента импульса в этом случае не зависит от времени:
 , совпадающим по направлению с угловой скоростью. Таким образом, при отсутствии момента внешних сил гироскоп сохраняет положение своей оси в пространстве.
, совпадающим по направлению с угловой скоростью. Таким образом, при отсутствии момента внешних сил гироскоп сохраняет положение своей оси в пространстве.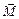 (в формуле (5.18)) обусловлен смещением центра тяжести системы и
(в формуле (5.18)) обусловлен смещением центра тяжести системы и Рис. 5.5
Рис. 5.5
 ,
, радиус-вектор, проведенный из точки О1 к точке приложения силы. Вектор
радиус-вектор, проведенный из точки О1 к точке приложения силы. Вектор  . (5.20)
. (5.20) за время dt совпадает по направлению с вектором
за время dt совпадает по направлению с вектором  . (5.21)
. (5.21) .
. (5.22)
(5.22)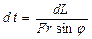 . (5.23)
. (5.23) , тогда
, тогда . (5.24)
. (5.24) ,
, . (5.25)
. (5.25) постоянно.
постоянно.
 .
.
